- CAT Courses
- Free Video Resources & Tests
Video Resources
...
- Super 75
- CAT Past Papers
- Free Study Material
- BlogsDecember 23, 2025
XAT Time Management Tips 2026
December 21, 2025XAT Decision Making & GK Guide with PYQs for 2026 Prep
- Results
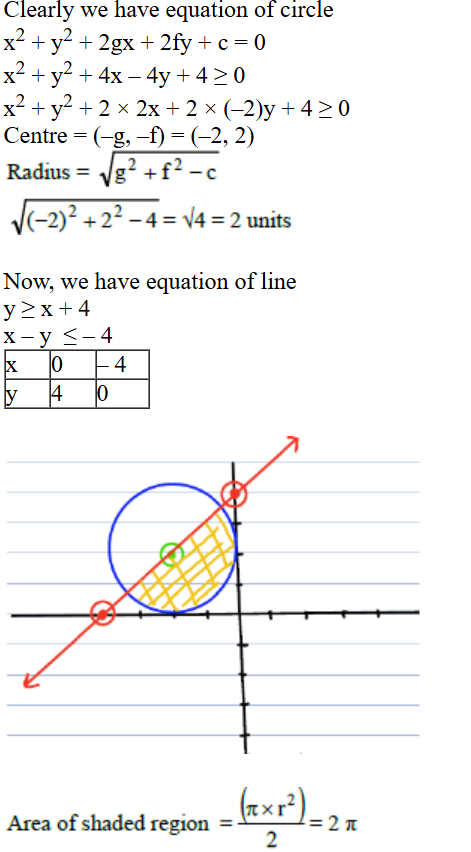
In the XY -plane, the area, in sq. units, of the region defined by the inequalities y ≥ x + 4 and – 4 ≤ x2 + y2 + 4(x-y) ≤ 0 is

Correct Answer
Option B
The sum of all real values of k for which
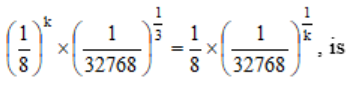
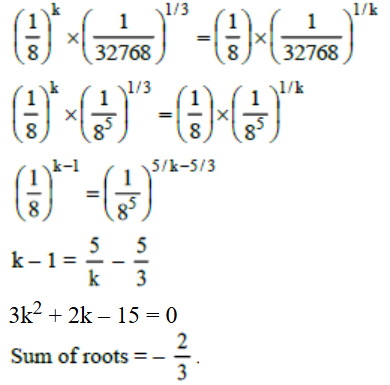
Correct Answer
Option D
Here to form all 4-digit numbers using the distinct non-zero digits a, b, c, d and each digit appears exactly once in each position across all permutations. The total number of 4 – digit numbers is 4! = 24 Each digit appears 24/4 = 6 times in each place (thousands, hundreds, tens, and units) For a given digit x, its total contributions are, x × (1000 + 100 + 10 + 1) × 6 = x × 1111 × 6 = 6666x. The sum of all numbers is: 6 × 1111 × (a + b + c + d) = 6666 (a + b + c + d). 6666 (a + b + c + d) = 153310 + n, where n is a single-digit natural number. Divide 153310 by 6666 ⇒ a + b + c + d = 153310/6666 = 23 (approx) ⇒ 6666 × 23 = 153318 ⇒ 153310 + n = 153318 ⇒ n = 153318 – 153310 = 8 The value of a + b + c + d + n = 23 + 8 = 31
Correct Answer
31
Total number of hours for which Renu worked is 15 × 4 = 60 hrs Total number of hours for which Seema worked is 8 × 5 = 40 hrs Total work is taken as LCM of (60, 40) = 120 units Efficiency of Renu is 120/60 = 2 units/hours Efficiency of Seema is 120/40 = 2 units/hours As per the question Renu works 2 hours per day, So Seema works for 4 hours per day. Total work completed by Renu is 2 × 2 = 4 units/day Total work completed by Seema is 3 × 4 = 12 units/day As per the question number of day taken by Renu is double of Seema. Let number of day taken by Seema is ‘x’ so number of days taken by Renu is ‘2x’. Total work will be completed by 4 × 2x + 12x = 120 x = 6 days.
Correct Answer
6
Question is based on GINT, largest integer not exceeding √n. Find the value of a1 + a2 +….+a50. When n = 1, √1= 1 n = 2, √2= 1 n = 3, √3= 1 n = 4, √4= 2 So, we need to count it like this, from 1 to 3 we have 1 three times so total will be 1 × 3 = 3 from 4 to 8 we have 2 five times so total will be 2 × 5 = 10 from 9 to 15 we have 3 seven times so total will be 3 × 7 = 21 from 16 to 24 we have 4 nine times so total will be 4 × 9 = 36 from 25 to 35 we have 5 eleven times so total will be 5 × 11 = 55 from 36 to 48 we have 6 thirteen times so total will be 6 × 13 = 78 from 49 to 50 we have 7 two times so total will be 7 × 2 = 14 Hence, answer will be 3 + 10 + 21 + 36 + 55 + 78 + 14 = 217
Correct Answer
217
Total surface area of cuboid = 2(lb + bh + hl)
⇒ 2(lb + bh + hl) = 846 cm2
The sum of lengths of all the edges = 4(l + b + h) =144
⇒ l + b + h = 36cm
Now, (l + b + h)2 = l2 + b2 + h2 + 2(lb + bh + hl)
⇒ l2 + b2 + h2 = (l + b + h)2 – 2(lb + bh + hl)
⇒ l2 + b2 + h2 = 362 – 846 = 1296 – 846 = 450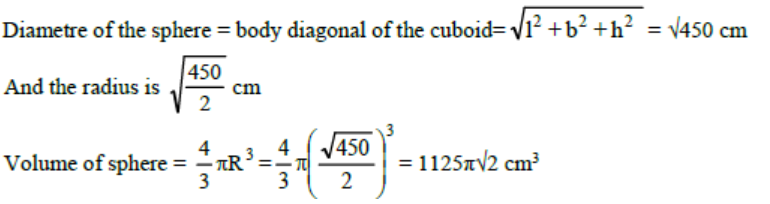
Correct Answer
Option B
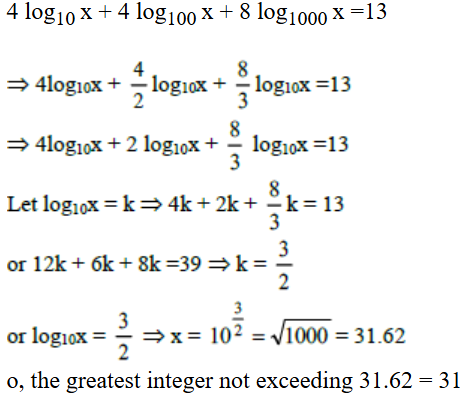
Correct Answer
31
If (a + b √n) is the positive square root of (29 − 12 √5), where a and b are integers, and n is a natural number, then the maximum possible value of (a + b + n) is
(29 - 12√5) = (a + b√n)2 (29 - 12√5) must be a square of (x-y)2 (x-y)2 = x2 + y2 + 2xy 2xy = 12√5 xy = 6√5 If we take x = 6 and y = √5 (6 - √5)2 = 36 + 5 - 12√5 = 41 - 12√5 ( not possible) If we take x = 3 and y = 2√5 (3 - 2√5)2 = 9 + 20 - 12√5 = 29 - 12√5 (possible) If we take x = 2√5 and y = 3 (2√5 - 3)2 = 20 + 9 - 12√5 = 29 - 12√5 (possible) If we take x = √20 and y = 3 (√20 - 3)2 = 20 + 9 - 12√5 = 29 - 12√5 (possible) If we take x = √20 and y = 3 (3 - √20)2 = 20 + 9 - 12√5 = 29 - 12√5 (possible) Positive root: (a + b√n)2 = (3 - 2√5)2 = a + b + n = 3 -2 + 5 = 6 Negative root: (a + b√n)2 = (2√5 - 3)2 = a + b + n = 2 + 5 – 3 = 4 Positive root: (a + b√n)2 = (-3 + √20)2 = a + b + n = -3 + 1 + 20 = 18 (Answer) Negative root: (a + b√n)2 = (3 - √20)2 = a + b + n = 3 – 1 + 20 = 22 As the question asked maximum possible value of positive root so answer is 18.
Correct Answer
Option D
Explanation: The best way to solve such questions is to move backwards. In the end he is left with nothing. Just see that to the last person he has given 1/2 of the grains and then 0 grains. In general person sells 1/2 of the grains and 3 kg more, so the person left with 1/2 of the grains and 3 kg less. x/2 – 3 = 0 x = 6 (before giving to third person) x/2 – 3 = 6 x = 18 (before giving to second person) x/2 – 3 = 18 x = 42 (before giving to first person) So the person initially have 42 kg of grains
Correct Answer
Option C
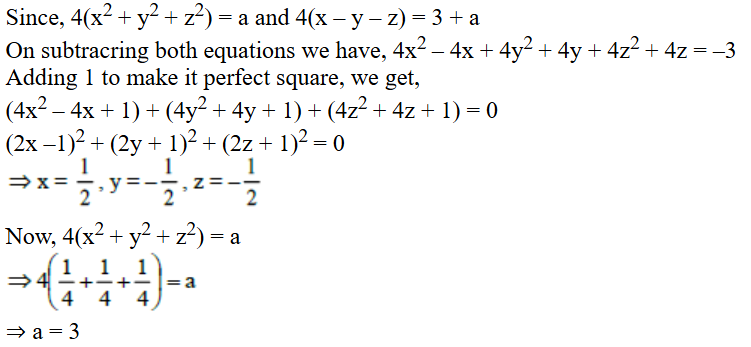
Correct Answer
Option B
Consider two sets A = {2,3,5, 7,11,13} and B = {1,8, 27}. Let f be a function from A to B such that for every element b in B, there is at least one element a in A such that f (a) = b. Then, the total number of such functions f is
Basically we are looking for onto function from A to B. Let n(A) = m, n(B) = n So, number of onto functions = nm – nC1(n – 1)m + nC2(n – 2)m – nC3(n – 3)m = 36 – 3C1(2)6 + 3C2(1)6 – 3C3(0) = 540
Correct Answer
Option D
Let the Initial CP = 100, Initial SP = Initial CP × 140% = 140. New CP = 60% of 100 = 60, New SP = 150% of 60 = 90. Difference between the Initial and New selling price is 140 – 90 = 50 Now we need to compare it with actual information as per the question, our 50 is representing 5 Rs as per question. 10 is representing 1Rs, 140 will represent 14 Rs.
Correct Answer
Option C
Let the four numbers be p, q, r, and s. By first condition, p+q/2 = p + 1 ⇒ q = p + 2 By second condition, p+q+r/3 = p+q/2 +2 ⇒ r = p + 7 By third condition, p+q+r+s/4 = p+q+r/3 +3 ⇒ s = p + 15 Thus the numbers are p, p + 2, p + 7 and p + 15. So, the difference between the largest and the smallest number = p + 15 – p = 15.
Correct Answer
15

Correct Answer
Option A
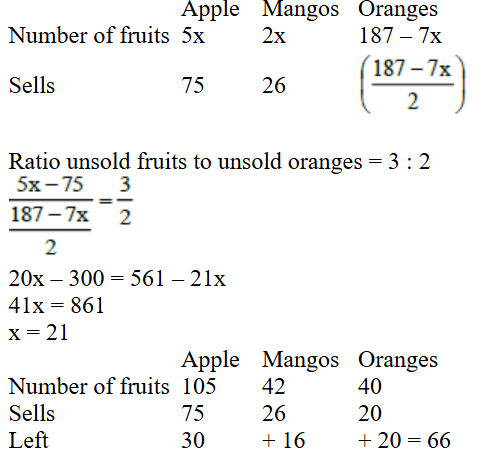
Correct Answer
66
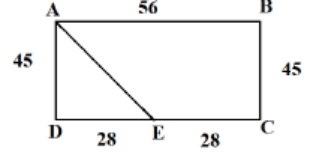 ABCD is a rectangle, E is a mid-point of D and C.
ΔADE is a right angle triangle by applying Pythagorean theorem, AE = 53.
Using the formula to calculate area of triangle = radius of incircle × Semi perimeter.
1/2 × 28 × 45 = r × (45+28+53/2)
r = 10
ABCD is a rectangle, E is a mid-point of D and C.
ΔADE is a right angle triangle by applying Pythagorean theorem, AE = 53.
Using the formula to calculate area of triangle = radius of incircle × Semi perimeter.
1/2 × 28 × 45 = r × (45+28+53/2)
r = 10
Correct Answer
10
If the equations x2 + mx + 9 = 0, x2 + nx + 17 = 0 and x2 + (m + n)x + 35 = 0 have a common negative root, then the value of (2m + 3n) is Let 𝛼 be the common negative root, then substitute it into each equation we have α2 + mα + 9 = 0…. (i), α2 + nα + 17 = 0…..(ii) and α2 + (m + n)α + 35 = 0….. (iii) Subtracting eq. (i) and (ii) we get α2 + nα + 17 − α2 − mα − 9 = 0 ⇒ (n − m)α + 8 = 0 α = - 8/n-m α2 + mα + 9 + α2 + nα + 17 = 0 ⇒ 2α2 + (m + n) α + 26 = 0 Subtract the third equation from the sum of the first and second equations, we get 2α2 + (m + n)α + 26 − α2 − (m + n)α − 35 = 0 α2 − 9 = 0 ⇒ α2 = 9 ⇒ α = ± 3, Since α is negative, α = −3 As α = - 8/n-m ⇒ -3 = - 8/n-m ⇒ n – m = 8/3 Substitute, α = −3 into the first equation, we get α2 + mα + 9 = 0 ⇒ 9 − 3m + 9 = 0 ⇒ m = 6 Substitute m = 6 in n – m = 8/3 ⇒ n – 6 = 8/3 ⇒ n = 26/3 Now 2m + 3n = 2 x 6 + 3 x 26/3 = 12 + 26 = 38
Correct Answer
38
Let the incomes of Kamal, Amal and Vimal in September be proportional to 8k, 6k, 5k respectively. The house rent paid by Kamal is 15% of 8k = 1.2k The house rent paid by Amal is 12% of 6k = 0.72k The house rent paid by Vimal is 18% of 5k = 0.9k Their total house rent = 1.2k + 0.72k + 0.9k = 2.82k In October their house rent remains same while their incomes increase by 10%, 12% and 15% respectively. Kamal's increased income = 8k × 1.1 = 8.8k Amal's increased income = 6k × 1.12 = 6.72k Vimal's increased income = 5k × 1.15 = 5.75k Total income in October = 8.8k + 6.72k + 5.75k = 21.27k The house rent remains the same at 2.82k. The percentage of their total income paid as rent in October = 2.82k / 21.27k × 100 = 13.26% (aprox.)
Correct Answer
Option B
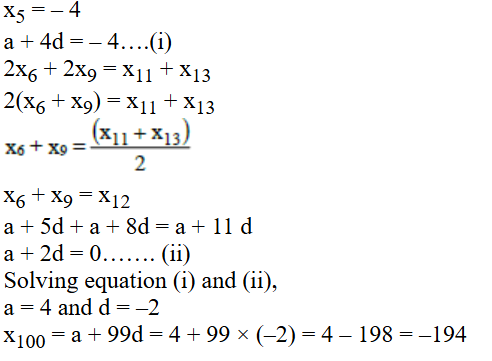
Correct Answer
Option D

Correct Answer
Option B

Correct Answer
Option C
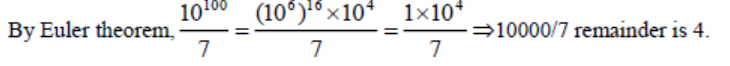
Correct Answer
Option C

We at Quantifiers understand and deliver on the personal attention each of our students requires. Whether it is through our pedagogy that enables non-engineers or non-math background students, our constant effort to proactively provide solutions, or our focus on our student’s goals.