CAT 2024 | DILR Set 1
Direction Q.1 to 5:
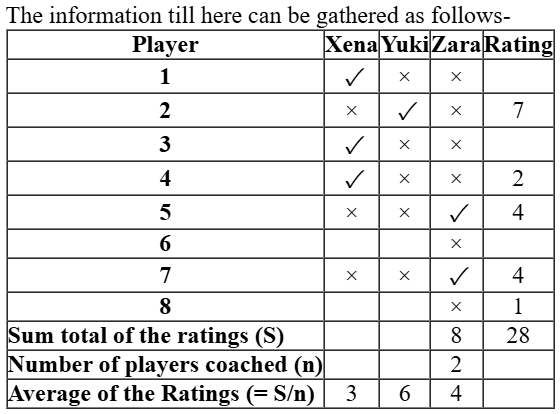
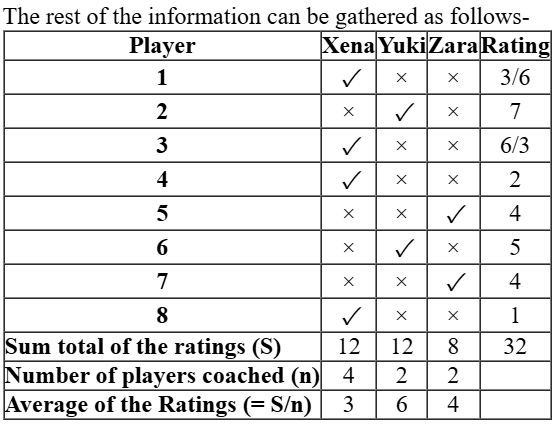
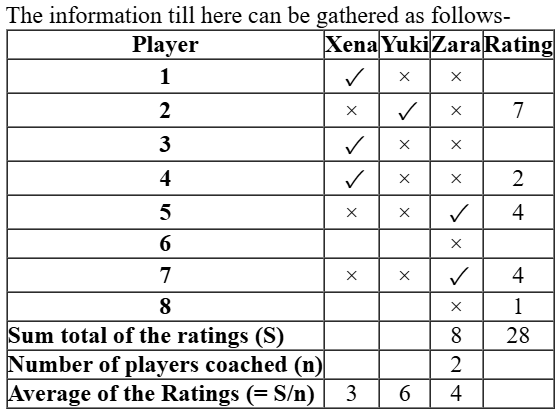
Eight gymnastics players numbered 1 through 8 underwent a training camp where they were coached by three coaches – Xena, Yuki, and Zara. Each coach trained at least two players. Yuki trained only even numbered players, while Zara trained only odd numbered players.
After the camp, the coaches evaluated the players and gave integer ratings to the respective players trained by them on a scale of 1 to 7, with 1 being the lowest rating and 7 the highest.
The following additional information is known.
- Xena trained more players than Yuki.
- Player-1 and Player-4 were trained by the same coach, while the coaches who trained Player-2, Player-3 and Player-5 were all different.
- Player-5 and Player-7 were trained by the same coach and got the same rating. All other players got a unique rating.
- The average of the ratings of all the players was 4.
- Player-2 got the highest rating.
- The average of the ratings of the players trained by Yuki was twice that of the players trained by Xena and two more than that of the players trained by Zara.
- Player-4’s rating was double of Player-8’s and less than Player-5’s.
1. What best can be concluded about the number of players coached by Zara?
- Exactly 2
- Either 2 or 3
- Exactly 3
- Either 2 or 3 or 4
Considering Yuki trained only even numbered players, so Yuki would not be training odd numbered player.
Similarly, Zara trained only odd numbered players, so Zara would not be training even numbered players.
From point 2, Player 1 and Player 4 were trained by same coach, this is not possible for Yuki and Zara, so both of them are trained by Xena
From point 3, Player 5 and Player 7 were trained by same coach, which is possible either for Xena or Zara.
But if Xena coaches player 5 and player 7, the only possible player left for Zara to coach would be player 3, but it is given that each coach rained at least two players.
So, Zara coached player 5 and player 7.
From point 2, Player 2, Player 3 and Player 5 trained by different coaches.
So, player 3 wouldn’t be coached by Zara as Zara coached player 5.
So, player 3 must be coached by Xena and player 2 must be coached by Yuki.
From point 3, Player 5 and Player 7 got the same rating = r (let) and rest all 6 players got unique ratings.
Also, from point 4, the average ratings of all the players = 4
So, the sum total of ratings of all the 8 players = 8 × 4 = 32
Sum of 7 unique integer values from 1 to 7 = 28
So, the value of same rating, r = 32 – 28 = 4
From point 5, player 2 got the highest rating = 7
From point 6, average of the ratings of the players trained by Zara = (4+4)2 = 4
So, average of the ratings of the players trained by Yuki = 4 + 2 = 6 and average of the ratings of the players trained by Xena = 62 = 3
Let the sum total of the ratings of Xena = X and the number of players coached
From point 7, player 4’s rating = 2 × player 8’s rating and player 4’s rating < player 5’s rating = 4
So, only possibility that player 4’s rating = 2 and player’s 8 rating = 1
Now, let the number of the players coached by Xena = m
So, the sum total of the ratings of the players coached by Xena = 3 × m = 3m
Also, the number of the players coached by Yuki = 8 – 2 – m = 6 – m
So, the sum total of the ratings of the players coached by Yuki = 6 × (6 – m) = 36 – 6m
Also we know, 3m + 36 – 6m + 8 = 32
Solving, m = 4
So, the number of the players coached by Yuki = 6 – m = 2 and the sum total of the ratings of the players coached by Yuki = 36 – 6m = 12
Now one among the 2 players coached by Yuki is player 2 who had a rating of 7, so the other player must have rating 12 – 7 = 5.
So, that player must be player 6 who had a rating of 5.
So, player 8 must be coached by Xena along with player 1, player 3 and player 4 and the rating of player 1 and player 3 would be either 3 or 6 in any order.
Zara coached exactly 2 players (Player 5 and Player 7)
2. What was the rating of Player-7?
Considering Yuki trained only even numbered players, so Yuki would not be training odd numbered player.
Similarly, Zara trained only odd numbered players, so Zara would not be training even numbered players.
From point 2, Player 1 and Player 4 were trained by same coach, this is not possible for Yuki and Zara, so both of them are trained by Xena
From point 3, Player 5 and Player 7 were trained by same coach, which is possible either for Xena or Zara.
But if Xena coaches player 5 and player 7, the only possible player left for Zara to coach would be player 3, but it is given that each coach rained at least two players.
So, Zara coached player 5 and player 7.
From point 2, Player 2, Player 3 and Player 5 trained by different coaches.
So, player 3 wouldn’t be coached by Zara as Zara coached player 5.
So, player 3 must be coached by Xena and player 2 must be coached by Yuki.
From point 3, Player 5 and Player 7 got the same rating = r (let) and rest all 6 players got unique ratings.
Also, from point 4, the average ratings of all the players = 4
So, the sum total of ratings of all the 8 players = 8 × 4 = 32
Sum of 7 unique integer values from 1 to 7 = 28
So, the value of same rating, r = 32 – 28 = 4
From point 5, player 2 got the highest rating = 7
From point 6, average of the ratings of the players trained by Zara = (4+4)/2 = 4
So, average of the ratings of the players trained by Yuki = 4 + 2 = 6 and average of the ratings of the players trained by Xena = 6/2 = 3
Let the sum total of the ratings of Xena = X and the number of players coached
From point 7, player 4’s rating = 2 × player 8’s rating and player 4’s rating < player 5’s rating = 4
So, only possibility that player 4’s rating = 2 and player’s 8 rating = 1
Now, let the number of the players coached by Xena = m
So, the sum total of the ratings of the players coached by Xena = 3 × m = 3m
Also, the number of the players coached by Yuki = 8 – 2 – m = 6 – m
So, the sum total of the ratings of the players coached by Yuki = 6 × (6 – m) = 36 – 6m
Also we know, 3m + 36 – 6m + 8 = 32
Solving, m = 4
So, the number of the players coached by Yuki = 6 – m = 2 and the sum total of the ratings of the players coached by Yuki = 36 – 6m = 12
Now one among the 2 players coached by Yuki is player 2 who had a rating of 7, so the other player must have rating 12 – 7 = 5.
So, that player must be player 6 who had a rating of 5.
So, player 8 must be coached by Xena along with player 1, player 3 and player 4 and the rating of player 1 and player 3 would be either 3 or 6 in any order.
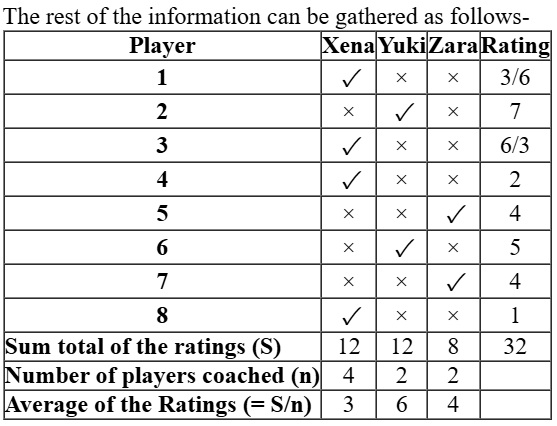The rating of player 7 = 4
3. What was the rating of Player-6?
Considering Yuki trained only even numbered players, so Yuki would not be training odd numbered player.
Similarly, Zara trained only odd numbered players, so Zara would not be training even numbered players.
From point 2, Player 1 and Player 4 were trained by same coach, this is not possible for Yuki and Zara, so both of them are trained by Xena
From point 3, Player 5 and Player 7 were trained by same coach, which is possible either for Xena or Zara.
But if Xena coaches player 5 and player 7, the only possible player left for Zara to coach would be player 3, but it is given that each coach rained at least two players.
So, Zara coached player 5 and player 7.
From point 2, Player 2, Player 3 and Player 5 trained by different coaches.
So, player 3 wouldn’t be coached by Zara as Zara coached player 5.
So, player 3 must be coached by Xena and player 2 must be coached by Yuki.
From point 3, Player 5 and Player 7 got the same rating = r (let) and rest all 6 players got unique ratings.
Also, from point 4, the average ratings of all the players = 4
So, the sum total of ratings of all the 8 players = 8 × 4 = 32
Sum of 7 unique integer values from 1 to 7 = 28
So, the value of same rating, r = 32 – 28 = 4
From point 5, player 2 got the highest rating = 7
From point 6, average of the ratings of the players trained by Zara = (4+4)2 = 4
So, average of the ratings of the players trained by Yuki = 4 + 2 = 6 and average of the ratings of the players trained by Xena = 62 = 3
Let the sum total of the ratings of Xena = X and the number of players coached
From point 7, player 4’s rating = 2 × player 8’s rating and player 4’s rating < player 5’s rating = 4
So, only possibility that player 4’s rating = 2 and player’s 8 rating = 1
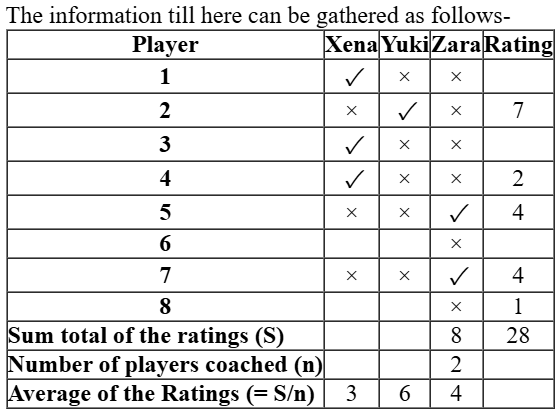Now, let the number of the players coached by Xena = m
So, the sum total of the ratings of the players coached by Xena = 3 × m = 3m
Also, the number of the players coached by Yuki = 8 – 2 – m = 6 – m
So, the sum total of the ratings of the players coached by Yuki = 6 × (6 – m) = 36 – 6m
Also we know, 3m + 36 – 6m + 8 = 32
Solving, m = 4
So, the number of the players coached by Yuki = 6 – m = 2 and the sum total of the ratings of the players coached by Yuki = 36 – 6m = 12
Now one among the 2 players coached by Yuki is player 2 who had a rating of 7, so the other player must have rating 12 – 7 = 5.
So, that player must be player 6 who had a rating of 5.
So, player 8 must be coached by Xena along with player 1, player 3 and player 4 and the rating of player 1 and player 3 would be either 3 or 6 in any order.
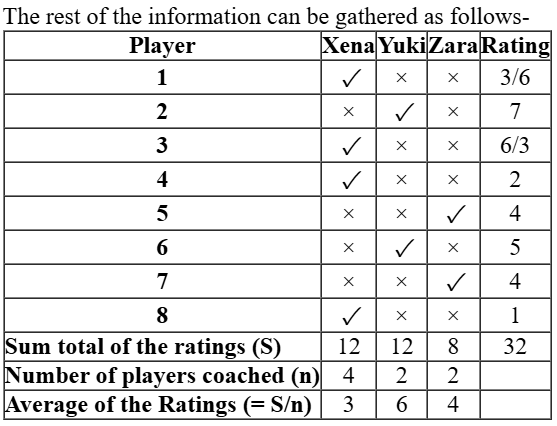The rating of player 6 = 5
4. For how many players the ratings can be determined with certainty?
Considering Yuki trained only even numbered players, so Yuki would not be training odd numbered player.
Similarly, Zara trained only odd numbered players, so Zara would not be training even numbered players.
From point 2, Player 1 and Player 4 were trained by same coach, this is not possible for Yuki and Zara, so both of them are trained by Xena
From point 3, Player 5 and Player 7 were trained by same coach, which is possible either for Xena or Zara.
But if Xena coaches player 5 and player 7, the only possible player left for Zara to coach would be player 3, but it is given that each coach rained at least two players.
So, Zara coached player 5 and player 7.
From point 2, Player 2, Player 3 and Player 5 trained by different coaches.
So, player 3 wouldn’t be coached by Zara as Zara coached player 5.
So, player 3 must be coached by Xena and player 2 must be coached by Yuki.
From point 3, Player 5 and Player 7 got the same rating = r (let) and rest all 6 players got unique ratings.
Also, from point 4, the average ratings of all the players = 4
So, the sum total of ratings of all the 8 players = 8 × 4 = 32
Sum of 7 unique integer values from 1 to 7 = 28
So, the value of same rating, r = 32 – 28 = 4
From point 5, player 2 got the highest rating = 7
From point 6, average of the ratings of the players trained by Zara = (4+4)2 = 4
So, average of the ratings of the players trained by Yuki = 4 + 2 = 6 and average of the ratings of the players trained by Xena = 62 = 3
Let the sum total of the ratings of Xena = X and the number of players coached
From point 7, player 4’s rating = 2 × player 8’s rating and player 4’s rating < player 5’s rating = 4
So, only possibility that player 4’s rating = 2 and player’s 8 rating = 1
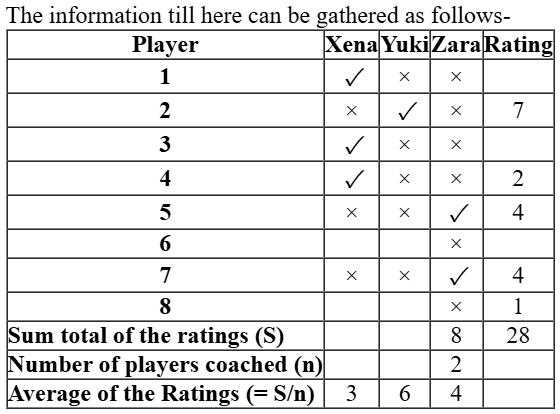Now, let the number of the players coached by Xena = m
So, the sum total of the ratings of the players coached by Xena = 3 × m = 3m
Also, the number of the players coached by Yuki = 8 – 2 – m = 6 – m
So, the sum total of the ratings of the players coached by Yuki = 6 × (6 – m) = 36 – 6m
Also we know, 3m + 36 – 6m + 8 = 32
Solving, m = 4
So, the number of the players coached by Yuki = 6 – m = 2 and the sum total of the ratings of the players coached by Yuki = 36 – 6m = 12
Now one among the 2 players coached by Yuki is player 2 who had a rating of 7, so the other player must have rating 12 – 7 = 5.
So, that player must be player 6 who had a rating of 5.
So, player 8 must be coached by Xena along with player 1, player 3 and player 4 and the rating of player 1 and player 3 would be either 3 or 6 in any order.
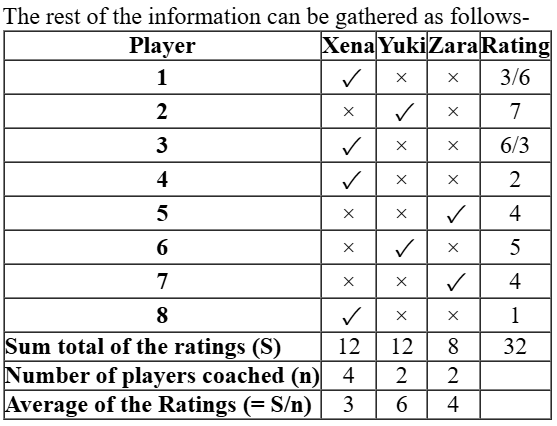For 6 players the ratings can be determined with certainty
5. Who all were the players trained by Xena?
- Player-1, Player-4, Player-6, Player-8
- Player-1, Player-3, Player-4, Player-6
- Player-1, Player-3, Player-4, Player-8
- Player-1, Player-3, Player-4
Considering Yuki trained only even numbered players, so Yuki would not be training odd numbered player.
Similarly, Zara trained only odd numbered players, so Zara would not be training even numbered players.
From point 2, Player 1 and Player 4 were trained by same coach, this is not possible for Yuki and Zara, so both of them are trained by Xena
From point 3, Player 5 and Player 7 were trained by same coach, which is possible either for Xena or Zara.
But if Xena coaches player 5 and player 7, the only possible player left for Zara to coach would be player 3, but it is given that each coach rained at least two players.
So, Zara coached player 5 and player 7.
From point 2, Player 2, Player 3 and Player 5 trained by different coaches.
So, player 3 wouldn’t be coached by Zara as Zara coached player 5.
So, player 3 must be coached by Xena and player 2 must be coached by Yuki.
From point 3, Player 5 and Player 7 got the same rating = r (let) and rest all 6 players got unique ratings.
Also, from point 4, the average ratings of all the players = 4
So, the sum total of ratings of all the 8 players = 8 × 4 = 32
Sum of 7 unique integer values from 1 to 7 = 28
So, the value of same rating, r = 32 – 28 = 4
From point 5, player 2 got the highest rating = 7
From point 6, average of the ratings of the players trained by Zara = (4+4)2 = 4
So, average of the ratings of the players trained by Yuki = 4 + 2 = 6 and average of the ratings of the players trained by Xena = 62 = 3
Let the sum total of the ratings of Xena = X and the number of players coached
From point 7, player 4’s rating = 2 × player 8’s rating and player 4’s rating < player 5’s rating = 4
So, only possibility that player 4’s rating = 2 and player’s 8 rating = 1
Now, let the number of the players coached by Xena = m
So, the sum total of the ratings of the players coached by Xena = 3 × m = 3m
Also, the number of the players coached by Yuki = 8 – 2 – m = 6 – m
So, the sum total of the ratings of the players coached by Yuki = 6 × (6 – m) = 36 – 6m
Also we know, 3m + 36 – 6m + 8 = 32
Solving, m = 4
So, the number of the players coached by Yuki = 6 – m = 2 and the sum total of the ratings of the players coached by Yuki = 36 – 6m = 12
Now one among the 2 players coached by Yuki is player 2 who had a rating of 7, so the other player must have rating 12 – 7 = 5.
So, that player must be player 6 who had a rating of 5.
So, player 8 must be coached by Xena along with player 1, player 3 and player 4 and the rating of player 1 and player 3 would be either 3 or 6 in any order.
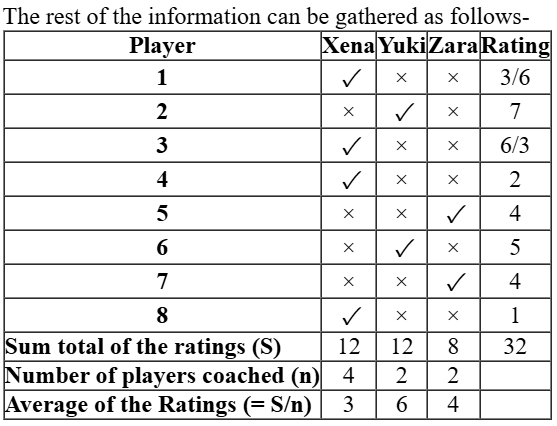The players trained by Xena are Player 1, Player 3, Player 4 and Player 8
CAT 2024 | DILR Set 2
Direction Q.6 to 9:
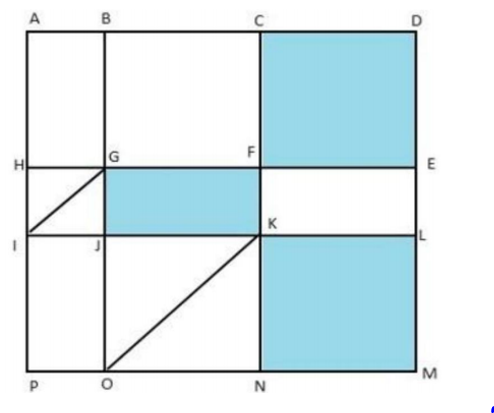
The above is a schematic diagram of walkways (indicated by all the straight-lines) and lakes (3 of them, each in the shape of rectangles – shaded in the diagram) of a gated area. Different points on the walkway are indicated by letters (A through P ) with distances being OP =150 m, ON = MN = 300 m, ML = 400 m, EL = 200 m, DE = 400 m.
The following additional information about the facilities in the area is known.
- The only entry/exit point is at C.
- There are many residences within the gated area; all of them are located on the path AH and 𝑀𝐿 with four of them being at 𝐴, 𝐻, 𝑀, and 𝐿.
- The post office is located at 𝑃 and the bank is located at 𝐵.
6. One resident whose house is located at 𝐿, needs to visit the post office as well as the bank. What is the minimum distance (in m) he has to walk starting from his residence and returning to his residence after visiting both the post office and the bank?
- 3200
- 3000
- 3000
- 2700
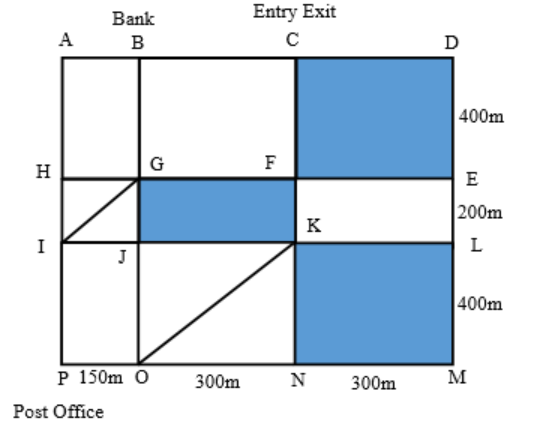In right angled triangle KNO, KN2 + ON2 = KO2
KN = ML = 400 m and ON = 300 m
So, KO2 = 4002 + 3002 = 250000 => KO = 500 m
Similarly, in right angled triangle GJI, IG2 = GJ2 + IJ2 = 2002 + 1502 = 62500 => IG = 250 m
The shortest path required would be L – K – O – P – I – G – B – C – F – E – L
The minimum distance walked = LK + KO + OP + PI + IG + GB + BC + CF + FE + EL
= 300 + 500 + 150 + 400 + 250 + 400 + 300 + 400 + 300 + 200 = 3200 m
7. One person enters the gated area and decides to walk as much as possible before leaving the area without walking along any path more than once and always walking next to one of the lakes. Note that he may cross a point multiple times. How much distance (in m) will he walk within the gated area?
- 3200
- 2800
- 3000
- 3800
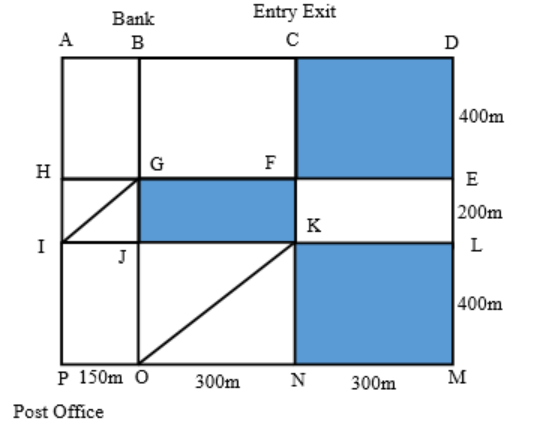In right angled triangle KNO, KN2 + ON2 = KO2
KN = ML = 400 m and ON = 300 m
So, KO2 = 4002 + 3002 = 250000 => KO = 500 m
Similarly, in right angled triangle GJI, IG2 = GJ2 + IJ2 = 2002 + 1502 = 62500 => IG = 250 m
The possible path would be C – D – E – F – K – L – M – N – K – J – G – F – C
The distance walked = 300 + 400 + 300 + 200 + 300 + 400 + 300 + 400 + 300 + 200 + 300 + 400 = 3800 m
8. One resident takes a walk within the gated area starting from 𝐴 and returning to 𝐴 without going through any point (other than 𝐴 ) more than once. What is the maximum distance (in m) she can walk in this way?
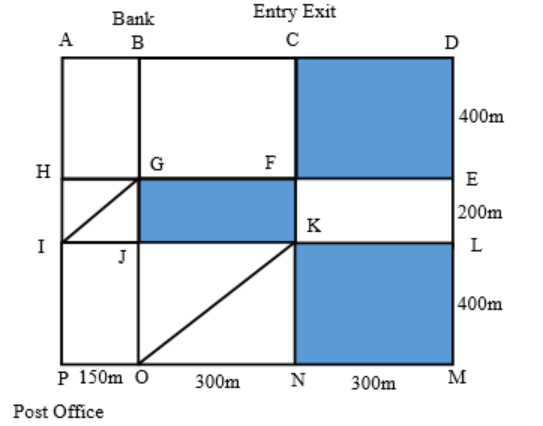In right angled triangle KNO, KN2 + ON2 = KO2
KN = ML = 400 m and ON = 300 m
So, KO2 = 4002 + 3002 = 250000 => KO = 500 m
Similarly, in right angled triangle GJI, IG2 = GJ2 + IJ2 = 2002 + 1502 = 62500 => IG = 250 m
The possible path would be A – B – G – F – C – D – E – L – M – N – K – J – O – P – I – H – A
The maximum distance walked = 150 + 400 + 300 + 400 + 300 + 400 + 200 + 400 + 300 + 400 + 300 + 400 + 150 + 400 + 200 + 400 = 5100
9. Visitors coming for morning walks are allowed to enter as long as they do not pass by any of the residences and do not cross any point (except C) more than once. What is the maximum distance (in m) that such a visitor can walk within the gated area?
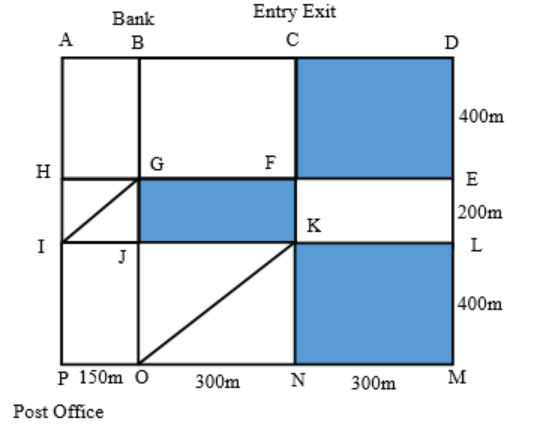In right angled triangle KNO, KN2 + ON2 = KO2
KN = ML = 400 m and ON = 300 m
So, KO2 = 4002 + 3002 = 250000 => KO = 500 m
Similarly, in right angled triangle GJI, IG2 = GJ2 + IJ2 = 2002 + 1502 = 62500 => IG = 250 m
The possible path would be C – D – E – F – K – N – O – P – I – J – G – B – C
The maximum distance walked = 300 + 400 + 300 + 200 + 400 + 300 + 150 + 400 + 150 + 200 + 400 + 300 = 3500 m
CAT 2024 | DILR Set 3
Direction Q.10 to 13:
An online e-commerce firm receives daily integer product ratings from 1 through 5 given by buyers. The daily average is the average of the ratings given on that day. The cumulative average is the average of all ratings given on or before that day.
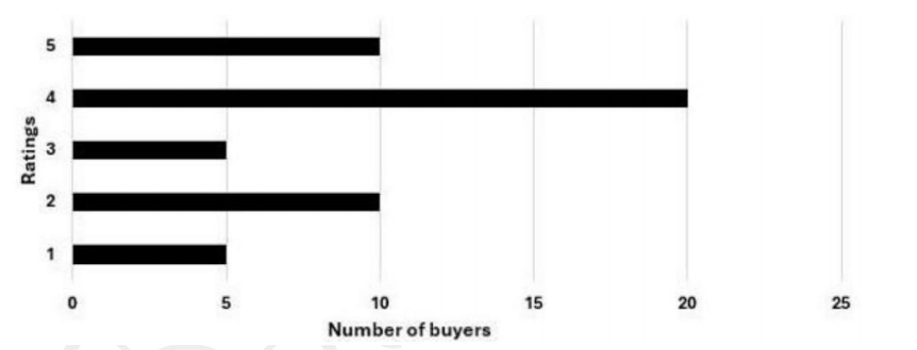
The rating system began on Day 1, and the cumulative averages were 3 and 3.1 at the end of Day 1 and Day 2, respectively. The distribution of ratings on Day 2 is given in the figure below.
Distribution of Ratings on Day 2
The following information is known about ratings on Day 3.
- 100 buyers gave product ratings on Day 3.
- The modes of the product ratings were 4 and 5 .
- The numbers of buyers giving each product rating are non-zero multiples of 10.
- The same number of buyers gave product ratings of 1 and 2, and that number is half the number of buyers who gave a rating of 3.
10. How many buyers gave ratings on Day 1?
From the Bar Chart, the total sum of ratings given on Day 2 by all the buyers = 5 × 1 + 10 × 2 + 5 × 3 + 20 × 4 + 10 × 5 = 170 Total number of ratings given by buyers on Day 2 = 5 + 10 + 5 + 20 + 10 = 50 So, the average rating on Day 2 = 170/50 = 3.4 Let the number of ratings given by buyers on Day 1 = x Sum of ratings on Day 1 = 3x Also given, (3x+170)/50= 3.1 Solving, 3x + 170 = 3.1x + 155 => x = 150 The number of buyers gave ratings on Day 1 = 150
11. What is the daily average rating of Day 3?
- 3.2
- 3.6
- 3.0
- 3.5
The total number of buyers gave ratings = 100
Let the number of buyers gave product ratings of 1 = 10y = ratings of 2
So, the number of buyers gave product ratings of 3 = 20y
Also, the modes of the product ratings were 4 and 5
Let the number of buyers gave product ratings of 4 = 10z = ratings of 5
Solving, 10y + 10y + 20y + 10z + 10z = 100
=> 4y + 2z = 10 => 2y + z = 5
Now, 10z to be mode, z = 3 and y = 1 (only possibility)
Total sum ratings on Day 3 = 10 × 1 + 10 × 2 + 20 × 3 + 30 × 4 + 30 × 5 = 360
The daily average rating on Day 3 = 360/100 = 3.6
12. What is the median of all ratings given on Day 3?
On Day 3,
The total number of buyers gave ratings = 100
Let the number of buyers gave product ratings of 1 = 10y = ratings of 2
So, the number of buyers gave product ratings of 3 = 20y
Also, the modes of the product ratings were 4 and 5
Let the number of buyers gave product ratings of 4 = 10z = ratings of 5
Solving, 10y + 10y + 20y + 10z + 10z = 100
=> 4y + 2z = 10 => 2y + z = 5
Now, 10z to be mode, z = 3 and y = 1 (only possibility)
The median of all the ratings given on Day 3 will be the average of 50th and 51th value which is same = 4
13. Which of the following is true about the cumulative average ratings of Day 2 and Day 3 ?
- The cumulative average of Day 3 decreased from Day 2.
- The cumulative average of Day 3 increased by more than 8% from Day 2.
- The cumulative average of Day 3 increased by less than 5% from Day 2.
- The cumulative average of Day 3 increased by a percentage between 5% and 8% from Day 2.
From the Bar Chart, the total sum of ratings given on Day 2 by all the buyers
= 5 × 1 + 10 × 2 + 5 × 3 + 20 × 4 + 10 × 5 = 170
Total number of ratings given by buyers on Day 2 = 5 + 10 + 5 + 20 + 10 = 50
So, the average rating on Day 2 = 170/50= 3.4
Let the number of ratings given by buyers on Day 1 = x
Sum of ratings on Day 1 = 3x
Also given, (3x+170)/50= 3.1
Solving, 3x + 170 = 3.1x + 155
=> x = 150
On Day 3,
The total number of buyers gave ratings = 100
Let the number of buyers gave product ratings of 1 = 10y = ratings of 2
So, the number of buyers gave product ratings of 3 = 20y
Also, the modes of the product ratings were 4 and 5
Let the number of buyers gave product ratings of 4 = 10z = ratings of 5
Solving, 10y + 10y + 20y + 10z + 10z = 100
=> 4y + 2z = 10 => 2y + z = 5
Now, 10z to be mode, z = 3 and y = 1 (only possibility)
Total sum ratings on Day 3 = 10 × 1 + 10 × 2 + 20 × 3 + 30 × 4 + 30 × 5 = 360
The cumulative average rating of Day 2 = 3.1 (given)
The cumulative average rating of Day 3 =
= (450+170+360)/(150+50+100) = 49/15
Percentage change from Day 2 to Day 3 = (49/15 – 3.1)/3.1 × 100 ≈ 5.38%
Hence, the cumulative average of Day 3 increased by a percentage between 5% and 8% from Day 2.
CAT 2024 | DILR Set 4
Direction Q.14 to 18:
The numbers 1,2,3,4,5,6,7,8,9, and 10 are placed in ten slots of the following grid based on the conditions below.
- Numbers in any row appear in an increasing order from left to right.
- Numbers in any column appear in a decreasing order from top to bottom.
- 1 is placed either in the same row or in the same column as 10
- Neither 2 nor 3 is placed in the same row or in the same column as 10.
- Neither 7 nor 8 is placed in the same row or in the same column as 9.
- 4 and 6 are placed in the same row.
14. What is the row number which has the least sum of numbers placed in that row?
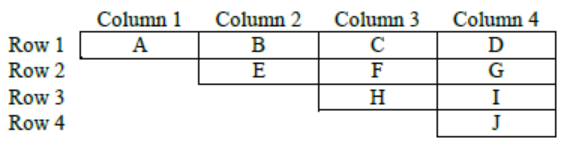
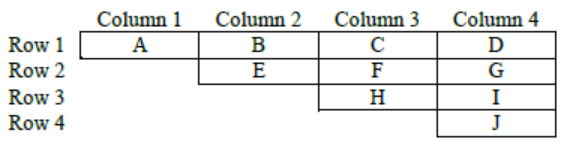
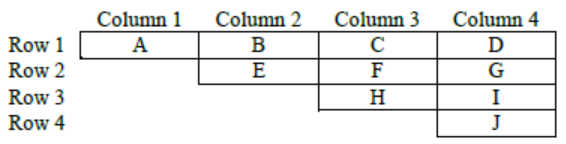
Let each of the ten slots is represented by the letters A to J as shown below-
Now considering point 1 and 2,
A, E, H, J < B, F, I < C, G < D
So, definitely the value of D = 10
The value of C or G = 8 or 9
The value of B, F or I = 5, 6 or 7
The value of A, E, H or J = 1, 2, 3 or 4
From point 3, 1 is placed either in the same row or in the same column as 10
So, either A = 1 or J = 1
From point 4, neither 2 nor 3 is placed in the same row or in the same column as 10.
So, A, B, C, G, I and J cannot have value 2 or 3.
So, E, F or H can have value 2 or 3, but F cannot have value 2 or 3.
So, either E or H = 2 or 3. So, A or J have value 1 or 4.
Also, from point 6, 4 and 6 are placed in the same row.
So, J cannot have value 4 as that is the only slot in Row 4.
So, A = 4 and J = 1
So, the value of B = 6 (only possibility) as C cannot have value 6
Now, from point 5, neither 7 nor 8 is placed in the same row or in the same column as 9.
So, if G = 9, either F or I has to be 7 which is placed in the same row or column of G, not possible.
So, C is definitely 9 and G is 8 and I is 7 and F is 5
Regarding E and H, we have following two possibilities-
The row number which has the least sum of numbers is placed in row 4
15. Which of the following statements MUST be true? I. 10 is placed in a slot in Row 1. II. 1 is placed in a slot in Row 4.
- Only II
- Both I and II
- Only I
- Neither I nor II
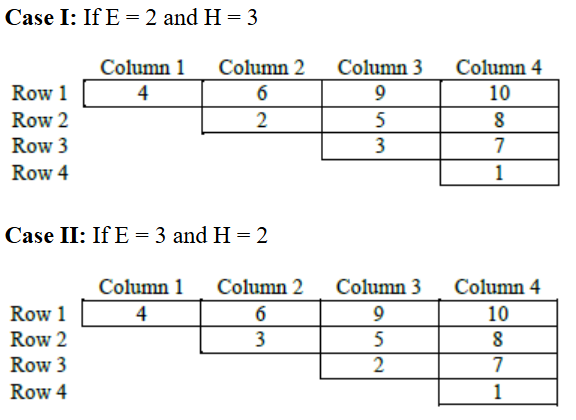
Let each of the ten slots is represented by the letters A to J as shown below-
Now considering point 1 and 2,
A, E, H, J < B, F, I < C, G < D
So, definitely the value of D = 10
The value of C or G = 8 or 9
The value of B, F or I = 5, 6 or 7
The value of A, E, H or J = 1, 2, 3 or 4
From point 3, 1 is placed either in the same row or in the same column as 10
So, either A = 1 or J = 1
From point 4, neither 2 nor 3 is placed in the same row or in the same column as 10.
So, A, B, C, G, I and J cannot have value 2 or 3.
So, E, F or H can have value 2 or 3, but F cannot have value 2 or 3.
So, either E or H = 2 or 3. So, A or J have value 1 or 4.
Also, from point 6, 4 and 6 are placed in the same row.
So, J cannot have value 4 as that is the only slot in Row 4.
So, A = 4 and J = 1
So, the value of B = 6 (only possibility) as C cannot have value 6
Now, from point 5, neither 7 nor 8 is placed in the same row or in the same column as 9.
So, if G = 9, either F or I has to be 7 which is placed in the same row or column of G, not possible.
So, C is definitely 9 and G is 8 and I is 7 and F is 5
Regarding E and H, we have following two possibilities-
Statement I. 10 is placed in a slot in Row 1, true
Statement II. 1 is placed in a slot in Row 4, true
Hence, both statement I and II are true
16. Which of the following statements MUST be true? I. 2 is placed in a slot in Column 2. II. 3 is placed in a slot in Column 3.
- Neither I nor II
- Only I
- Both I and II
- Only II
Let each of the ten slots is represented by the letters A to J as shown below-
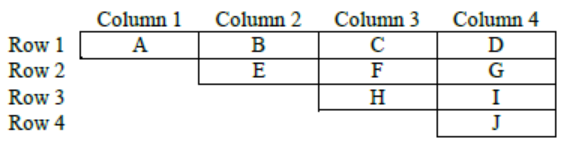Now considering point 1 and 2,
A, E, H, J < B, F, I < C, G < D
So, definitely the value of D = 10
The value of C or G = 8 or 9
The value of B, F or I = 5, 6 or 7
The value of A, E, H or J = 1, 2, 3 or 4
From point 3, 1 is placed either in the same row or in the same column as 10
So, either A = 1 or J = 1
From point 4, neither 2 nor 3 is placed in the same row or in the same column as 10.
So, A, B, C, G, I and J cannot have value 2 or 3.
So, E, F or H can have value 2 or 3, but F cannot have value 2 or 3.
So, either E or H = 2 or 3. So, A or J have value 1 or 4.
Also, from point 6, 4 and 6 are placed in the same row.
So, J cannot have value 4 as that is the only slot in Row 4.
So, A = 4 and J = 1
So, the value of B = 6 (only possibility) as C cannot have value 6
Now, from point 5, neither 7 nor 8 is placed in the same row or in the same column as 9.
So, if G = 9, either F or I has to be 7 which is placed in the same row or column of G, not possible.
So, C is definitely 9 and G is 8 and I is 7 and F is 5
Regarding E and H, we have following two possibilities-
Statement I. 2 is placed in a slot in Column 2, may be or may not be true
Statement II. 3 is placed in a slot in Column 3, may be or may not be true
Hence, neither statement I nor II is true
17. For how many slots in the grid, placement of numbers CANNOT be determined with certainty?
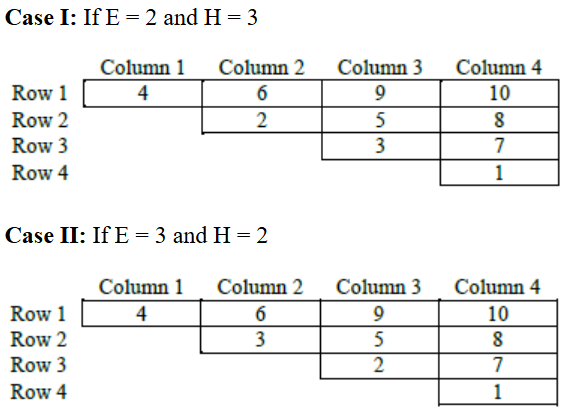
Let each of the ten slots is represented by the letters A to J as shown below-
Now considering point 1 and 2,
A, E, H, J < B, F, I < C, G < D
So, definitely the value of D = 10
The value of C or G = 8 or 9
The value of B, F or I = 5, 6 or 7
The value of A, E, H or J = 1, 2, 3 or 4
From point 3, 1 is placed either in the same row or in the same column as 10
So, either A = 1 or J = 1
From point 4, neither 2 nor 3 is placed in the same row or in the same column as 10.
So, A, B, C, G, I and J cannot have value 2 or 3.
So, E, F or H can have value 2 or 3, but F cannot have value 2 or 3.
So, either E or H = 2 or 3. So, A or J have value 1 or 4.
Also, from point 6, 4 and 6 are placed in the same row.
So, J cannot have value 4 as that is the only slot in Row 4.
So, A = 4 and J = 1
So, the value of B = 6 (only possibility) as C cannot have value 6
Now, from point 5, neither 7 nor 8 is placed in the same row or in the same column as 9.
So, if G = 9, either F or I has to be 7 which is placed in the same row or column of G, not possible.
So, C is definitely 9 and G is 8 and I is 7 and F is 5
Regarding E and H, we have following two possibilities-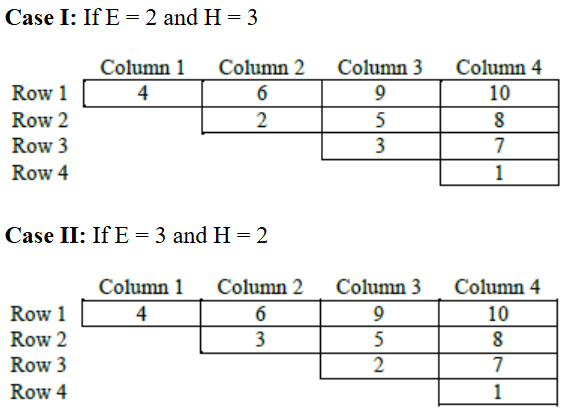
For 2 slots (Row 2, Column 2 and Row 3, Column 3) in the grid where the placement of numbers cannot be determined with certainty.
18. What is the sum of the numbers placed in Column 4?
Let each of the ten slots is represented by the letters A to J as shown below-
Now considering point 1 and 2,
A, E, H, J < B, F, I < C, G < D
So, definitely the value of D = 10
The value of C or G = 8 or 9
The value of B, F or I = 5, 6 or 7
The value of A, E, H or J = 1, 2, 3 or 4
From point 3, 1 is placed either in the same row or in the same column as 10
So, either A = 1 or J = 1
From point 4, neither 2 nor 3 is placed in the same row or in the same column as 10.
So, A, B, C, G, I and J cannot have value 2 or 3.
So, E, F or H can have value 2 or 3, but F cannot have value 2 or 3.
So, either E or H = 2 or 3. So, A or J have value 1 or 4.
Also, from point 6, 4 and 6 are placed in the same row.
So, J cannot have value 4 as that is the only slot in Row 4.
So, A = 4 and J = 1
So, the value of B = 6 (only possibility) as C cannot have value 6
Now, from point 5, neither 7 nor 8 is placed in the same row or in the same column as 9.
So, if G = 9, either F or I has to be 7 which is placed in the same row or column of G, not possible.
So, C is definitely 9 and G is 8 and I is 7 and F is 5
Regarding E and H, we have following two possibilities-
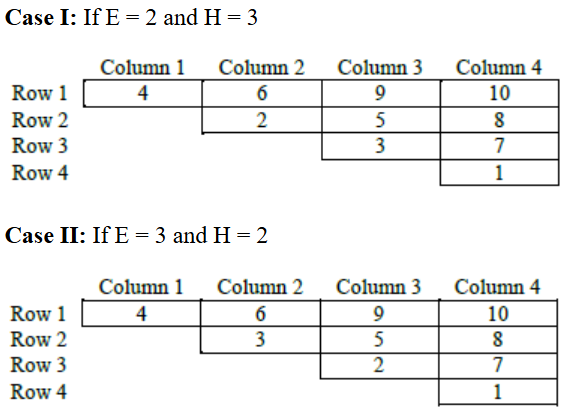The sum of the numbers placed in Column 4 = 10 + 8 + 7 + 1 = 26
CAT 2024 | DILR Set 5
Direction Q.19 to 22:
The two plots below give the following information about six firms A, B, C, D, E, and F for 2019 and 2023.
PAT: The firm’s profits after taxes in Rs. crores,
ES: The firm’s employee strength, that is the number of employees in the firm, and
PRD: The percentage of the firm’s PAT that they spend on Research and Development (R&D).
In the plots, the horizontal and vertical coordinates of point representing each firm gives their ES and PAT values respectively. The PRD values of each firm are proportional to the areas around the points representing each firm. The areas are comparable between the two plots, i.e., equal areas in the two plots represent the same PRD values for the two years.
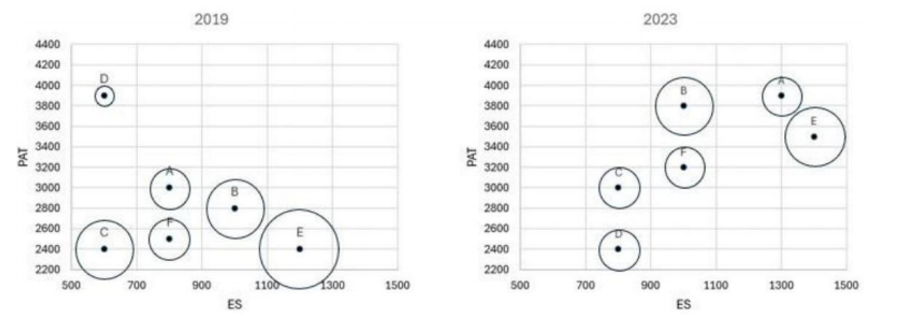
19. Assume that the annual rate of growth in PAT over the previous year (ARG) remained constant over the years for each of the six firms. Which among the firms A, B, C, and E had the highest ARG?
- Firm E
- Firm B
- Firm A
- Firm C
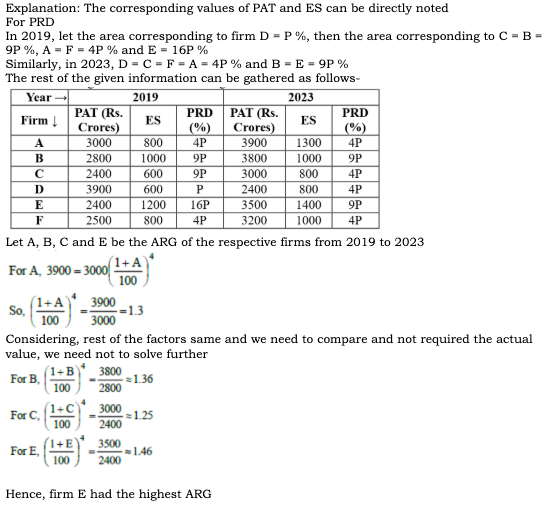
20. The ratio of the amount of money spent by Firm C on R&D in 2019 to that in 2023 is closest to
- 5: 6
- 9: 5
- 5: 9
- 9: 4
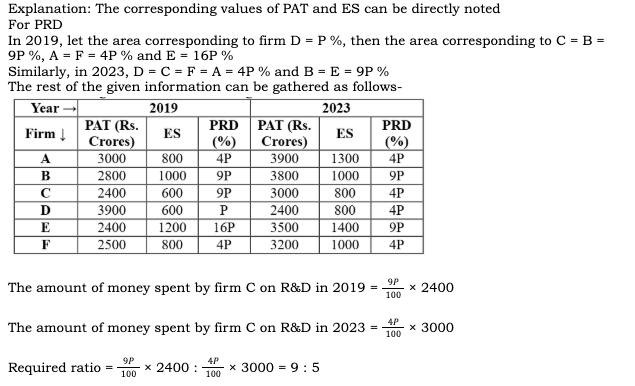
21. Which among the firms A, C, E, and F had the maximum PAT per employee in 2023?
- Firm C
- Firm A
- Firm F
- Firm E
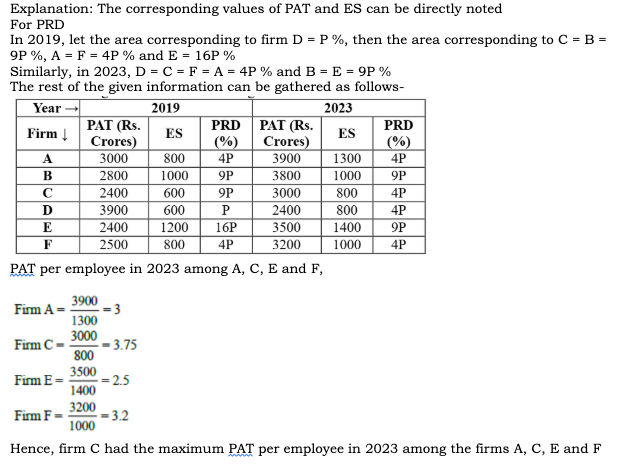
22. Which among the firms C, D, E, and F had the least amount of R&D spending per employee in 2023?
- Firm E
- Firm D
- Firm F
- Firm C
The corresponding values of PAT and ES can be directly noted
For PRD
In 2019, let the area corresponding to firm D = P %, then the area corresponding to C = B = 9P %, A = F = 4P % and E = 16P %
Similarly, in 2023, D = C = F = A = 4P % and B = E = 9P %
The rest of the given information can be gathered as follows-
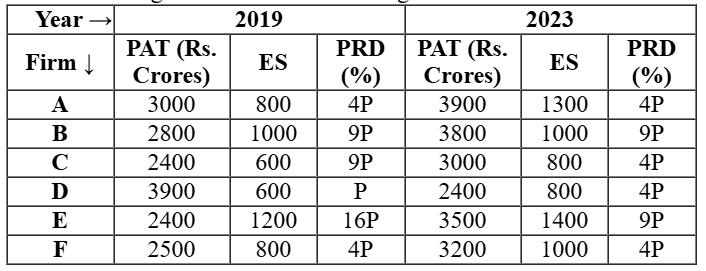PRD per employee in 2023 among the firms C, D, E and F
Firm C = (4P/100 × 3000)/800 = 0.15P
Firm D = (4P/100 × 2400)/800 = 0.12P
Firm E = (9P/100 × 3500)/1400 = 0.225P
Firm F = (4P/100 × 3200)/1000 = 0.128P
Hence, firm D had the least PRD per employee in 2023 among the firms C, D, E and F
