A sum of money is split among Amal, Sunil and Mita so that the ratio of the shares of Amal and Sunil is 3:2, while the ratio of the shares of Sunil and Mita is 4:5. If the difference between the largest and the smallest of these three shares is Rs 400, then Sunil’s share, in rupees, is
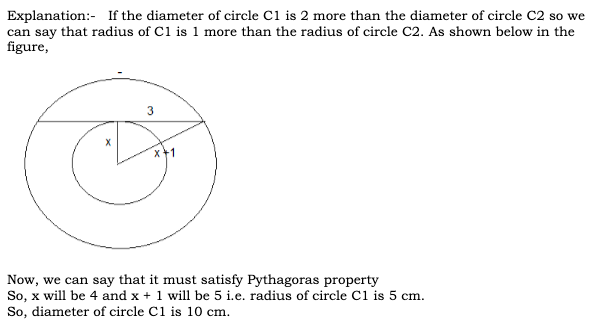
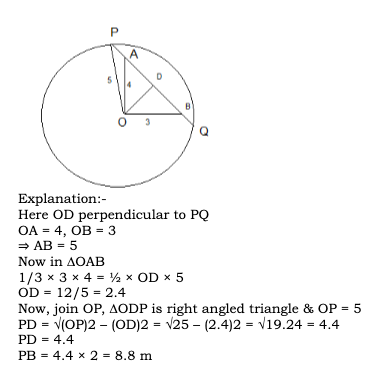
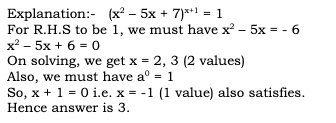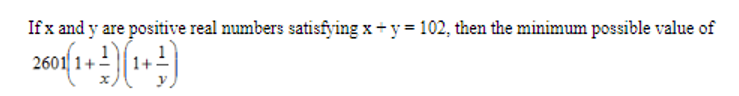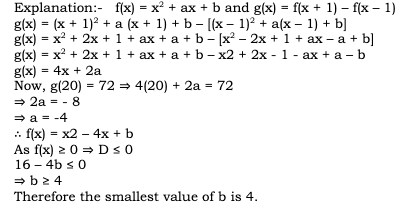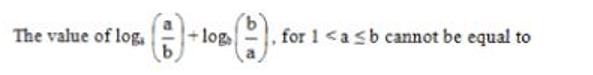Given that Amal : Sunil = 3 : 2. Also, Sunil : Mita = 4 : 5 On combining the ratio we get Amal : Sunil : Mita = 6 : 4 : 5 So, let their shares be 6x, 4x and 5x According to the question 6x – 4x = 400 2x = 400 x = 200 So, Sunil’s share = 4x = 4 × 200 = 800
For the same principal amount, the compound interest for two years at 5% per annum exceeds the simple interest for three years at 3% per annum by Rs. 1125.Then the principal amount in rupees is
Let the principal = 8000 So, simple interest for 3 years @ 3% per annum = Rs.720 Compound interest for 2 years @ 5% per annum = Rs.820 Difference = Rs.100 So, using unitary method When difference is 100 principal is 8000 When difference is 1125 principal is 90000
Aron bought some pencils and sharpeners. Spending the same amount of money as Aron, Aditya bought twice as many pencils and 10 less sharpeners. If the cost of one sharpener is Rs. 2 more than the cost of a pencil, then the minimum possible number of pencils bought by Aron and Aditya together is
Let the cost of pencil is Rs. x and of sharpener is Rs.(x+2) Let Aron bought ‘a’ pencils & ‘b’ sharpeners. Aditya bought ‘2a’ pencils & ‘b – 10’ sharpeners. Now, ax + b(x + 2) = 2ax + (b – 10)(x + 2) ax + bx + 2b = 2ax + bx + 2b – 10x – 20 ax – 10x = 20 a – 10 = 20/x a = 20/x + 10 Now ‘a’ is minimum when ‘x’ is maximum i.e. x = 20 Minimum ‘a’ = 20/20 + 10 = 11 Total pencils = 3a = 3 × 11 = 33
In May, John bought the same amount of rice and the same amount of wheat as he had bought in April, but spent Rs. 150 more due to price increase of rice and wheat by 20%and 12%, respectively. If John had spent Rs. 450 on rice in April, then how much did he spend on wheat in May?
Given that John had spent Rs.450 in April and it is being given that in May price of rice is increased by 20%. So, price of rice is increased by 90 (20% of 450). And it is given that in May he had Rs.150 more out of which 90 is for rice. So, for wheat he had spend Rs.60 more (150 – 90). 12% of original price in April = 60 100% of original price in April = 500. So, he spend on wheat in may = 500 + 12% of 500 = 560
How many 4-digit numbers, each greater than 1000 and each having all four digits distinct, are there with 7 coming before 3?
Case I: When 7 is at first place then 3 can be any of the three places = 1 × 1 × 8 × 7 + 1 × 8 × 1 × 7 + 1 × 8 × 7 × 1 = 168 Case II: When 3 is at the last place = 7 × 1 × 7 × 1 + 7 × 7 × 1 × 1 = 98 Case III: When both 7 and 3 are in middle places = 7 × 1 × 1 × 7 = 49 So, total cases = 168 + 98 + 49 = 315
Two circular tracks T1 and T2 of radii 100 m and 20 m, respectively touch at a point A. Starting from A at the same time, Ram and Rahim are walking on track T1 and track T2at speeds 15 km/hr and 5 km/hr respectively. The number of full rounds that Ram will make to meet Rahim again for the first time is
Ratio of time taken by Ram and Rahim in covering one full round = 2 π × 100 × 18/15 × 5 : 2 π × 20 × 18/5 × 5 = 5:3 So, minimum number of rounds to be taken by Ram and Rahim to meet are 3 & 5 respectively. So, the number of full rounds that Ram will make to meet Rahim again for the first time is 3.
The sum of the perimeters of an equlateral triangle and a rectangle is 90 cm the area, T, of the triangle and the area, R, of the rectangle, both in sq cm, satisfy the relationship R = T2. If the sides of the rectangle are in the ratio 1:3, then the length, in cm, of the longer side of the rectangle, is
Let the ratio be x. So, the dimensions of rectangle is x and 3x and let the side of equilateral triangle be ‘a’ Perimeter of rectangle = 2 (x + 3x) = 8x Perimeter of equilateral triangle = 3a According to the question: 3a + 8x = 90 _______ (1) Also, given that relation R = T2, where R is area of rectangle and T is area of equilateral triangle So, we have 3x2 = (√3/4 a2)2 x = a2/4 Substituting x in eq”(1), we have 2a2 + 3a – 90 = 0 On solving, we get a = 6 Hence, x = 9 So, longer side of rectangle = 3x = 3 × 9 = 27
The distance from B to C is thrice that from A to B. Two trains travel from A to C via B. The speed of train 2 is double that of train 1 while traveling from A to B and their speeds are interchanged while traveling from B to C. The ratio of the time taken by train 1 to that taken by train 2 in travelling from A to C is
In a group of 10 students, the mean of the lowest 9 scores is 42 while the mean of the highest 9 scores is 47. For the entire group of 10 students, the maximum possible mean exceeds the minimum possible mean by
Difference between highest number – Lowest number = 9 × 47 – 9 × 42 = 45 Maximum possible value of highest number = 42 + 45 = 87 Minimum possible value of lowest number = 47 – 45 = 2 So, Maximum possible mean = [42 × 9 + 87]/10 = 46.5 Minimum possible mean = [47 × 9 + 2]/10 = 42.5 Required difference = 46.5 – 42.5 = 4
A and B are two points on a straight line. Ram runs from A to B while Rahim runs from B to A. After crossing each other, Ram and Rahim reach their destinations in one minute and four minutes, respectively. If they start at the same time, then the ratio of Ram’s speed to Rahim’s speed is
As we know that if two objects P and Q start at the same time in opposite direction from point A and B respectively. After passing each other, P reaches B in x seconds and Q reaches A in y seconds then, Speed of P: Speed of Q = √b : √a So, Ram’s speed : Rahim’s speed = √4 : √1 = 2 : 1
In a car race, car A beats car B by 45 km, car B beats car C by 50km, and car A beats C by 90 km. the distance (in km) over which the race has been conducted is
Let A travels = x B travels = x – 45 C travels = x – 90 So, when B covers (x – 45) then C covers (x – 90) When B covers x = (x – 90)/(x – 45) × x = (x – 50) On solving, we get x = 450
Students in a college have to choose at least two subjects from Chemistry, Mathematics and Physics. The number of students choosing all three subjects is 18, choosing Mathematics as one of their subjects is 23 and choosing Physics as one of their subjects is 25. The smallest possible number of students who could choose Chemistry as one of their subjects is
Anil buys 12 toys and labels each with the same selling price. He sells 8 toys initially at 20% discount on the labeled price. Then he sells the remaining 4 toys at an additional 25% discount on the discounted price. Thus, he gets a total of Rs 2112, and makes a 10% profit. With no discounts, his percentage of profit would have been
Let x be the total purchase price of all articles and y be the marked price of one article. So, according to the question: 8 × 0.8 × y + 4 × 0.75 × 0.8 × y = 2112 On solving, we get y = 240 Given, 2112 = 1.10x x = 1920 If no discount is given, then 12 × 240 = 2880 Required % = 2880 – 1920/1920 = 50%
John takes twice as much time as Jack to finish a job. Jack and Jim together take one-thirds of the time to finish the job than John takes working alone. Moreover, in order to finish the job, John takes three days more than that taken by three of them working together. In how many days will Jim finish the job working alone?
Since John takes twice as much as Jack to finish a job. So, efficiency of John and jack is 1:2. Also, Jack and Jim together take one-third of the time to finish the job than John. So, efficiency of Jack + Jim and John is 3:1. So, efficiency of John, Jack and Jim is 1:2:1 respectively. Now, let all of them together took ‘x’ days so John alone take x + 3 days. So, x (1 + 2 + 1) = x + 3 On solving, we get x = 1 So, John takes = 4 days, Jack = 4/2 = 2 days and Jim = 4 days
If x and y are non-negative integers such that x + 9 = z, y + 1 = z and x + y < z + 5,then the maximum possible value of 2x + y ?
x + 9 = z ______ (1) y + 1 = z _______ (2) Adding (1) and (2), we get x + y +10 = 2z ⇒ x + y = 2z – 10 Now, x + y < z + 5 2z – 10 < z + 5 z < 15 Therefore, Maximum z = 14 From eq”(1), Maximum x = z – 9 = 5 From eq”(2), Maximum y = z – 1 = 13 Max.(2x + y) = 2 × 5 + 13 = 23
Let C be a circle of radius 5 meters having center at O. Let PQ be a chord of C that passes through points A and B where A is located 4 meters north of O and B is located3 meters east of O. Then, the length of PQ, in meters, is nearest to
We at Quantifiers understand and deliver on the personal attention each of our students requires. Whether it is through our pedagogy that enables non-engineers or non-math background students, our constant effort to proactively provide solutions, or our focus on our student’s goals.
