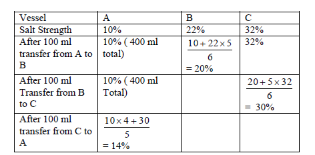
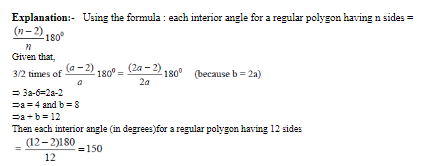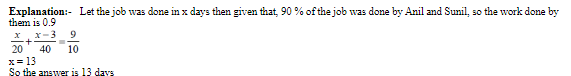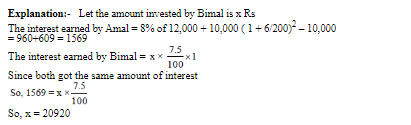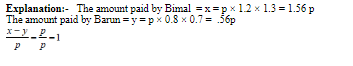Vessel A Contains 50 gm of salt and 450 ml water
vessel B contains 110 gm of salt and 390 ml water
vessel C contains 160 gm of salt & 340 ml water
After the transfer of 100 ml from A to B
A will contain 360 ml water & 40 gm salt and B will contain 120 gm of salt and 480 ml water which makes B having 20% salt strength. After the transfer of 100 ml from B to C, C will Contain 180 gm of salt & 420 ml of water making it have salt strength = 30% After the final transfer of 100 ml from C to A, A will contain 70 gm of salt and 430 ml water making the salt strength in A = 14%
Alternate method:-
 Answer = 14%
Answer = 14%
- CAT Courses
- Free Video Resources & Tests
Video Resources
...
- Super 75
- CAT Past Papers
- Free Study Material
- BlogsJanuary 7, 2026
GDPI Topics for MBA: 100 Important Topics for CAT 2025–26
January 6, 2026GDPI Preparation 2025 – Complete Strategy to Convert MBA Calls
- Results













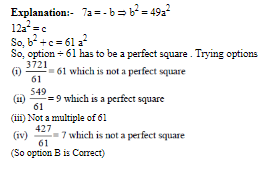
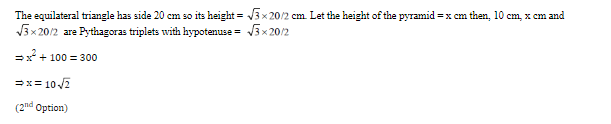
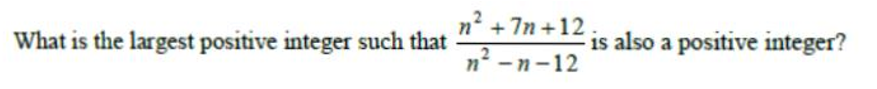
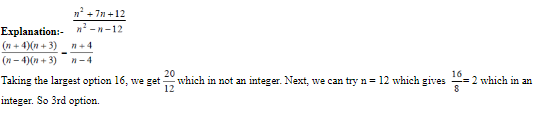
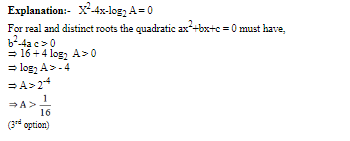
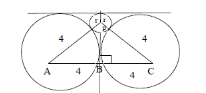 Considers ∆ APB having right angle at B
AP = 4 + r
BP = 4 – r
AB = 4
Applying Pythagoras theorem
(4+r)2 = ( 4 –r)2 + 42
⇒ (4+r)2 – (4-r)2=16
⇒ 16r=16
⇒ r= 1 cm
Considers ∆ APB having right angle at B
AP = 4 + r
BP = 4 – r
AB = 4
Applying Pythagoras theorem
(4+r)2 = ( 4 –r)2 + 42
⇒ (4+r)2 – (4-r)2=16
⇒ 16r=16
⇒ r= 1 cm
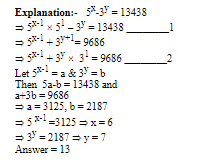

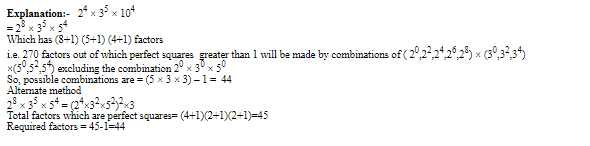

 ≈ 7%
≈ 7%