CAT 2021 DILR - Slot 2 Past Year Questions
CAT 2021 | DILR Set 1
DIRECTIONS for the question: Analyse the graph/s given below and answer the question that follows.
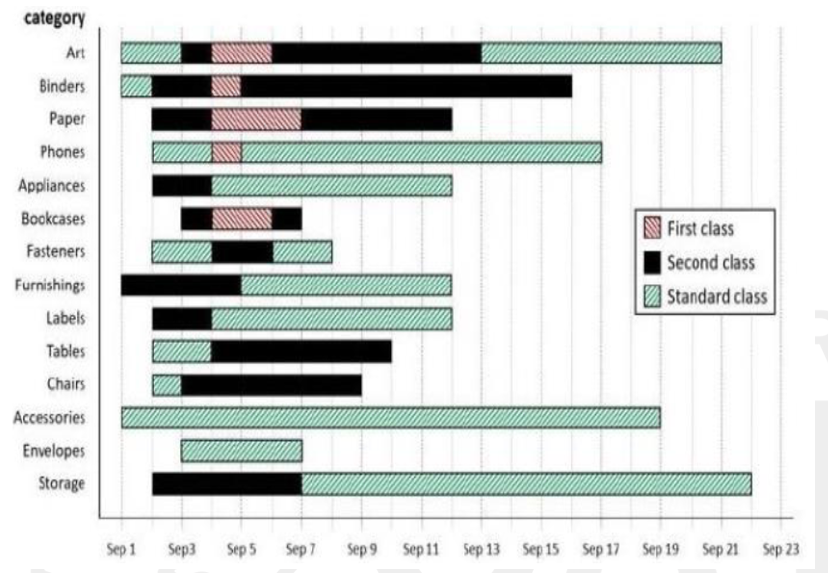
The different bars in the diagram above provide information about different orders in various categories (Art, Binders, ….) that were booked in the first two weeks of September of a store for one client. The colour and pattern of a bar denotes the ship mode (First Class / Second Class / Standard Class). The left end point of a bar indicates the booking day of the order, while the right end point indicates the dispatch day of the order. The difference between the dispatch day and the booking day (measured in terms of the number of days) is called the processing time of the order. For the same category, an order is considered for booking only after the previous order of the same category is dispatched. No two consecutive orders of the same category had identical ship mode during this period.
For example, there were only two orders in the furnishing category during this period. The first one was shipped in the Second Class. It was booked on Sep 1 and dispatched on Sep 5. The second order was shipped in the Standard class. It was booked on Sep 5 (although the order might have been placed before that) and dispatched on Sep 12. So the processing times were 4 and 7 days respectively for these orders.
1. How many days between Sep 1 and Sep 14 (both inclusive) had no booking from this client considering all the above categories? (in numerical value)
From the given information, we can make the following table. The numbers here are the dates on which the orders are booked (B) and dispatched (D).
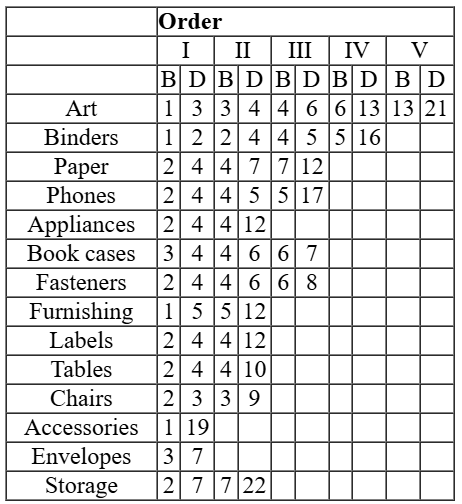 From the above table, we can see that no booking was done on 8th, 9th, 10th, 11th, 12th and 14th Sept. Therefore, for 6 days there was no booking.
From the above table, we can see that no booking was done on 8th, 9th, 10th, 11th, 12th and 14th Sept. Therefore, for 6 days there was no booking.
2. What was the average processing time of all orders in the categories which had only one type of ship mode? (in numerical value)
From the given information, we can make the following table. The numbers here are the dates on which the orders are booked (B) and dispatched (D).
 Accessories and Envelopes have only one type of shipping mode.
Processing time for Accessories = (19 - 1) = 18 days
Processing time for Envelopes = (7 - 3) = 4 days
Therefore, average time = 18+4/2 = 11 days
Accessories and Envelopes have only one type of shipping mode.
Processing time for Accessories = (19 - 1) = 18 days
Processing time for Envelopes = (7 - 3) = 4 days
Therefore, average time = 18+4/2 = 11 days
3. The sequence of categories -- Art, Binders, Paper and Phones -- in decreasing order of average processing time of their orders in this period is:
- Paper, Binders, Art, Phones
- Phones, Art, Binders, Paper
- Art, Binders, Paper, Phones
- Phones, Binders, Art, Paper
From the given information, we can make the following table. The numbers here are the dates on which the orders are booked (B) and dispatched (D).


4. Approximately what percentage of orders had a processing time of one day during the period Sep 1 to Sep 22 (both dates inclusive)?
- 16%
- 22%
- 20%
- 25%
From the given information, we can make the following table. The numbers here are the dates on which the orders are booked (B) and dispatched (D).
 Total orders = 35
Orders with processing time of one day = 7
∴ Required % age = 7/35 × 100 = 20%
Total orders = 35
Orders with processing time of one day = 7
∴ Required % age = 7/35 × 100 = 20%
Correct Answer 1
6
Correct Answer 2
11
Correct Answer 3
Option B
Correct Answer 4
Option C
CAT 2021 | DILR Set 2
DIRECTIONS for the question: Read the information given below and answer the question that follows.
The game of Chango is a game where two people play against each other; one of them wins and the other loses, i.e., there are no drawn Chango games. 12 players participated in a Chango championship. They were divided into four groups: Group A consisted of Aruna, Azul, and Arif; Group B consisted of Brinda, Brij, and Biju; Group C consisted of Chitra, Chetan, and Chhavi; and Group D consisted of Dipen, Donna, and Deb.
Players within each group had a distinct rank going into the championship. The players have NOT been listed necessarily according to their ranks. In the group stage of the game, the second and third ranked players play against each other, and the winner of that game plays against the first ranked player of the group. The winner of this second game is considered as the winner of the group and enters a semi-final.
The winners from Groups A and B play against each other in one semi-final, while the winners from Groups C and D play against each other in the other semi-final. The winners of the two semi-finals play against each other in the final to decide the winner of the championship.
It is known that:
- Chitra did not win the championship.
- Aruna did not play against Arif. Brij did not play against Brinda.
- Aruna, Biju, Chitra, and Dipen played three games each, Azul and Chetan played two games each, and the remaining players played one game each.
5. Who among the following was DEFINITELY NOT ranked first in his/her group?
- Brij
- Aruna
- Dipen
- Chitra
3 games:- Aruna, Biju, Chira, Dipen 2 games:- Azul, Chetan 1 game:- Arif, Brinda, Brij, Chhavi, Donna, Deb Group A:- Arif played one game & Azul played 2 games ∴ 1st match →Arif vs Azul → Azul won 2nd match →Azul vs Aruna →Aruna won ∴ Aruna is Rank 1 player of group A. As Aruna played 3 matches and she played only one match in group 1, so the remaining two matches of Aruna are semifinal & final. ⇒ Aruna played final Group B:- Brinda & Brij played 1 match each, so Biju cannot be rank one player in Group B. This is because, if Biju is rank 1, then Brinda & Brij will play first match and winner of that match will play against Biju, so that person will play 2 matches, which is not possible. If Brinda is rank 1 player, then I match →Biju vs Brij ⇒ Biju won II match →Biju vs Brinda ⇒ Biju won If Brij is rank 1 player, then I match →Biju vs Brinda ⇒ Biju won II match →Biju vs Brij ⇒ Biju won So either Brij or Brinda is rank 1 player in group B and Biju played 2 matches in group. So the third match which Biju will play is semifinal. Group C:- Here Chhavi played one match and Chetan played 2 matches. So match I:- Chhavi vs Chetan ⇒ Chetan won match II:- Chitra vs Chetan ⇒ Chitra won if Chhavi plays with Chitra & Chitra beats her, then Chitra will beat Chetan also. In that case Chetan has played only one game which is not possible. Here Chitra had played one match in group and her remaining matches are semifinal & final. So Chitra played final. Group D:- Here Donna & Deb played one match each. So as discussed in Group B, Dipen cannot be rank 1 player. ∴ In group D, either Donna & Deb are rank 1 player & Dipen played 2 matches in group and his one match will be semifinal. Dipen is definitely not ranked first in his group.
6. Which of the following pairs must have played against each other in the championship?
- Donna, Chetan
- Azul, Biju
- Deb, Donna
- Chitra, Dipen
3 games:- Aruna, Biju, Chira, Dipen 2 games:- Azul, Chetan 1 game:- Arif, Brinda, Brij, Chhavi, Donna, Deb Group A:- Arif played one game & Azul played 2 games ∴ 1st match →Arif vs Azul → Azul won 2nd match →Azul vs Aruna →Aruna won ∴ Aruna is Rank 1 player of group A. As Aruna played 3 matches and she played only one match in group 1, so the remaining two matches of Aruna are semifinal & final. ⇒ Aruna played final Group B:- Brinda & Brij played 1 match each, so Biju cannot be rank one player in Group B. This is because, if Biju is rank 1, then Brinda & Brij will play first match and winner of that match will play against Biju, so that person will play 2 matches, which is not possible. If Brinda is rank 1 player, then I match →Biju vs Brij ⇒ Biju won II match →Biju vs Brinda ⇒ Biju won If Brij is rank 1 player, then I match →Biju vs Brinda ⇒ Biju won II match →Biju vs Brij ⇒ Biju won So either Brij or Brinda is rank 1 player in group B and Biju played 2 matches in group. So the third match which Biju will play is semifinal. Group C:- Here Chhavi played one match and Chetan played 2 matches. So match I:- Chhavi vs Chetan ⇒ Chetan won match II:- Chitra vs Chetan ⇒ Chitra won if Chhavi plays with Chitra & Chitra beats her, then Chitra will beat Chetan also. In that case Chetan has played only one game which is not possible. Here Chitra had played one match in group and her remaining matches are semifinal & final. So Chitra played final. Group D:- Here Donna & Deb played one match each. So as discussed in Group B, Dipen cannot be rank 1 player. ∴ In group D, either Donna & Deb are rank 1 player & Dipen played 2 matches in group and his one match will be semifinal. Chitra, Dipen
7. Who won the championship?
- Brij
- Cannot be determined
- Aruna
- Chitra
3 games:- Aruna, Biju, Chira, Dipen 2 games:- Azul, Chetan 1 game:- Arif, Brinda, Brij, Chhavi, Donna, Deb Group A:- Arif played one game & Azul played 2 games ∴ 1st match →Arif vs Azul → Azul won 2nd match →Azul vs Aruna →Aruna won ∴ Aruna is Rank 1 player of group A. As Aruna played 3 matches and she played only one match in group 1, so the remaining two matches of Aruna are semifinal & final. ⇒ Aruna played final Group B:- Brinda & Brij played 1 match each, so Biju cannot be rank one player in Group B. This is because, if Biju is rank 1, then Brinda & Brij will play first match and winner of that match will play against Biju, so that person will play 2 matches, which is not possible. If Brinda is rank 1 player, then I match →Biju vs Brij ⇒ Biju won II match →Biju vs Brinda ⇒ Biju won If Brij is rank 1 player, then I match →Biju vs Brinda ⇒ Biju won II match →Biju vs Brij ⇒ Biju won So either Brij or Brinda is rank 1 player in group B and Biju played 2 matches in group. So the third match which Biju will play is semifinal. Group C:- Here Chhavi played one match and Chetan played 2 matches. So match I:- Chhavi vs Chetan ⇒ Chetan won match II:- Chitra vs Chetan ⇒ Chitra won if Chhavi plays with Chitra & Chitra beats her, then Chitra will beat Chetan also. In that case Chetan has played only one game which is not possible. Here Chitra had played one match in group and her remaining matches are semifinal & final. So Chitra played final. Group D:- Here Donna & Deb played one match each. So as discussed in Group B, Dipen cannot be rank 1 player. ∴ In group D, either Donna & Deb are rank 1 player & Dipen played 2 matches in group and his one match will be semifinal. Aruna & Chitra reached the final. As Chitra did not win final, so Aruna must have won it.
8. Who among the following did NOT play against Chitra in the championship?
- Biju
- Aruna
- Dipen
- Chetan
3 games:- Aruna, Biju, Chira, Dipen 2 games:- Azul, Chetan 1 game:- Arif, Brinda, Brij, Chhavi, Donna, Deb Group A:- Arif played one game & Azul played 2 games ∴ 1st match →Arif vs Azul → Azul won 2nd match →Azul vs Aruna →Aruna won ∴ Aruna is Rank 1 player of group A. As Aruna played 3 matches and she played only one match in group 1, so the remaining two matches of Aruna are semifinal & final. ⇒ Aruna played final Group B:- Brinda & Brij played 1 match each, so Biju cannot be rank one player in Group B. This is because, if Biju is rank 1, then Brinda & Brij will play first match and winner of that match will play against Biju, so that person will play 2 matches, which is not possible. If Brinda is rank 1 player, then I match →Biju vs Brij ⇒ Biju won II match →Biju vs Brinda ⇒ Biju won If Brij is rank 1 player, then I match →Biju vs Brinda ⇒ Biju won II match →Biju vs Brij ⇒ Biju won So either Brij or Brinda is rank 1 player in group B and Biju played 2 matches in group. So the third match which Biju will play is semifinal. Group C:- Here Chhavi played one match and Chetan played 2 matches. So match I:- Chhavi vs Chetan ⇒ Chetan won match II:- Chitra vs Chetan ⇒ Chitra won if Chhavi plays with Chitra & Chitra beats her, then Chitra will beat Chetan also. In that case Chetan has played only one game which is not possible. Here Chitra had played one match in group and her remaining matches are semifinal & final. So Chitra played final. Group D:- Here Donna & Deb played one match each. So as discussed in Group B, Dipen cannot be rank 1 player. ∴ In group D, either Donna & Deb are rank 1 player & Dipen played 2 matches in group and his one match will be semifinal. Biju played semifinal against Aruna and lost it. So he cannot play against Chitra.
Correct Answer 5
Option C
Correct Answer 6
Option D
Correct Answer 7
Option C
Correct Answer 8
Option A
CAT 2021 | DILR Set 3
DIRECTIONS for the question: Study the following information carefully and answer the given question.
Ravi works in an online food-delivery company. After each delivery, customers rate Ravi on each of four parameters – Behaviour, Packaging, Hygiene, and Timeliness, on a scale from 1 to 9. If the total of the four rating points is 25 or more, then Ravi gets a bonus of Rs. 20 for that delivery. Additionally, a customer may or may not give Ravi a tip. If the customer gives a tip, it is either Rs. 30 or Rs. 50.
One day, Ravi made four deliveries – one to each of Atal, Bihari, Chirag and Deepak, and received a total of Rs. 120 in bonus and tips. He did not get both a bonus and a tip from the same customer.
The following additional facts are also known.
- In Timeliness, Ravi received a total of 21 points, and three of the customers gave him the same rating points in this parameter. Atal gave higher rating points than Bihari and Chirag in this parameter.
- Ravi received distinct rating points in Packaging from the four customers adding up to 29 points. Similarly, Ravi received distinct rating points in Hygiene from the four customers adding up to 26 points.
- Chirag gave the same rating points for Packaging and Hygiene.
- Among the four customers, Bihari gave the highest rating points in Packaging, and Chirag gave the highest rating points in Hygiene.
- Everyone rated Ravi between 5 and 7 in Behaviour. Unique maximum and minimum ratings in this parameter were given by Atal and Deepak respectively.
- If the customers are ranked based on ratings given by them in individual parameters, then Atal’s rank based on Packaging is the same as that based on Hygiene. This is also true for Deepak.
9. What was the minimum rating that Ravi received from any customer in any parameter? (in numerical value)
The total tip received is Rs. 120
Now 120 = 20 + 20 + 30 + 50 or 20 + 50 + 50 + 0 or 30 + 30 + 30 + 30
It is given that in Timeliness, Ravi received a total of 21 points. As per point 1, let Atal gave x points then Bihari, Chirag and Deepak will give y each, s.t. x > y & x + 3y = 21
⇒ (x, y) are (6, 5) or (9, 4)
Total of Packaging is 29 with all distinct ratings ⇒ 29 = 9 + 8 + 7 + 5
Hygiene also has distinct ratings with a total of 26.
Now 26 = 9 + 8 + 7 + 2 or 9 + 8 + 6 + 3 or 9 + 8 + 5 + 4 or 8 + 7 + 6 + 5
Point 4 says that Chirag gave highest rating to hygiene, and also rating of Chirag as per point 3 is same for packaging & hygiene. So Chirag cannot give rating 9 to packaging as Bihari is the one giving highest rating to packaging.
∴ Chirag will give highest rating of 8 to hygiene and therefore 26 = 8 + 7 + 6 + 5
Using the point 5, the partial table can be as follows: 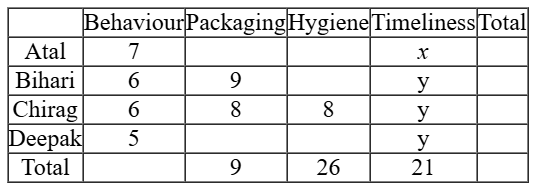 Point 6 says that Atal’s Rank in Packaging & hygiene is same. So it can be rank 3 or 4 and the same is true for Deepak also.
Two cases arise here:
Case I:- If Atal’s rank is 3rd in packaging and hygiene.
In this case Atal’s rating in packaging will be 7 and in hygiene will be 6 Deepak will be ranked 4 in these parameters with ratings 5 each.
Also taking the possible values of timeliness, the table will look like as follows
Point 6 says that Atal’s Rank in Packaging & hygiene is same. So it can be rank 3 or 4 and the same is true for Deepak also.
Two cases arise here:
Case I:- If Atal’s rank is 3rd in packaging and hygiene.
In this case Atal’s rating in packaging will be 7 and in hygiene will be 6 Deepak will be ranked 4 in these parameters with ratings 5 each.
Also taking the possible values of timeliness, the table will look like as follows
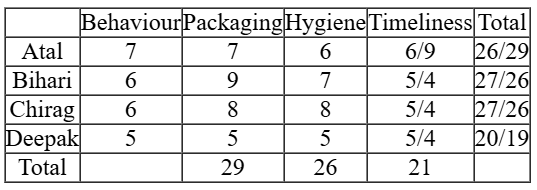 In this case Ravi will get bonus of Rs 20 each from Atal, Bihari & Chirag. From Deepak he can get maximum Rs 50 as tip. So his total will not be Rs 120 therefore, this case is wrong.
Case II:- If Atal’s rank is 4th in packaging and hygiene. In this case Atal’s ratings in these two parameters will be 5 each and Deepak’s rank will be third with ratings of 7 & 6 respectively in packaging and hygiene respect.
We get the first table as follows:
In this case Ravi will get bonus of Rs 20 each from Atal, Bihari & Chirag. From Deepak he can get maximum Rs 50 as tip. So his total will not be Rs 120 therefore, this case is wrong.
Case II:- If Atal’s rank is 4th in packaging and hygiene. In this case Atal’s ratings in these two parameters will be 5 each and Deepak’s rank will be third with ratings of 7 & 6 respectively in packaging and hygiene respect.
We get the first table as follows:
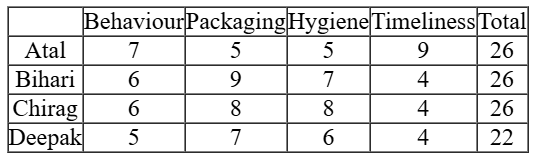 In this case again he will get Rs 20 bonus from Atal, Bihari & Chirag, so his total cannot be Rs 120. Hence this case is not valid.
If we take the second case of timeliness, then the table will be
In this case again he will get Rs 20 bonus from Atal, Bihari & Chirag, so his total cannot be Rs 120. Hence this case is not valid.
If we take the second case of timeliness, then the table will be
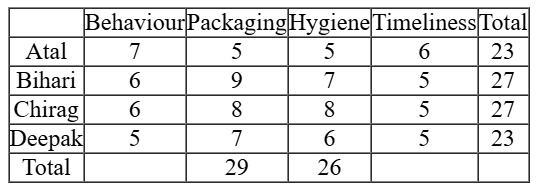 In this case Ravi can get tip from Atal & Deepak & will get bonus from Bihari & Chirag. Atal & Deepak can give tip of Rs 30 & Rs 50 in any order.
So he will get 120 = 20 + 20 + 30 + 50.
Minimum rating given is 5
In this case Ravi can get tip from Atal & Deepak & will get bonus from Bihari & Chirag. Atal & Deepak can give tip of Rs 30 & Rs 50 in any order.
So he will get 120 = 20 + 20 + 30 + 50.
Minimum rating given is 5
10. The COMPLETE list of customers who gave the maximum total rating points to Ravi is
- Atal and Bihari
- Bihari
- Atal
- Bihari and Chirag
The total tip received is Rs. 120
Now 120 = 20 + 20 + 30 + 50 or 20 + 50 + 50 + 0 or 30 + 30 + 30 + 30
It is given that in Timeliness, Ravi received a total of 21 points. As per point 1, let Atal gave x points then Bihari, Chirag and Deepak will give y each, s.t. x > y & x + 3y = 21
⇒ (x, y) are (6, 5) or (9, 4)
Total of Packaging is 29 with all distinct ratings ⇒ 29 = 9 + 8 + 7 + 5
Hygiene also has distinct ratings with a total of 26.
Now 26 = 9 + 8 + 7 + 2 or 9 + 8 + 6 + 3 or 9 + 8 + 5 + 4 or 8 + 7 + 6 + 5
Point 4 says that Chirag gave highest rating to hygiene, and also rating of Chirag as per point 3 is same for packaging & hygiene. So Chirag cannot give rating 9 to packaging as Bihari is the one giving highest rating to packaging.
∴ Chirag will give highest rating of 8 to hygiene and therefore 26 = 8 + 7 + 6 + 5
Using the point 5, the partial table can be as follows:
 Point 6 says that Atal’s Rank in Packaging & hygiene is same. So it can be rank 3 or 4 and the same is true for Deepak also.
Two cases arise here:
Case I:- If Atal’s rank is 3rd in packaging and hygiene.
In this case Atal’s rating in packaging will be 7 and in hygiene will be 6 Deepak will be ranked 4 in these parameters with ratings 5 each.
Also taking the possible values of timeliness, the table will look like as follows
Point 6 says that Atal’s Rank in Packaging & hygiene is same. So it can be rank 3 or 4 and the same is true for Deepak also.
Two cases arise here:
Case I:- If Atal’s rank is 3rd in packaging and hygiene.
In this case Atal’s rating in packaging will be 7 and in hygiene will be 6 Deepak will be ranked 4 in these parameters with ratings 5 each.
Also taking the possible values of timeliness, the table will look like as follows
 In this case Ravi will get bonus of Rs 20 each from Atal, Bihari & Chirag. From Deepak he can get maximum Rs 50 as tip. So his total will not be Rs 120 therefore, this case is wrong.
Case II:- If Atal’s rank is 4th in packaging and hygiene. In this case Atal’s ratings in these two parameters will be 5 each and Deepak’s rank will be third with ratings of 7 & 6 respectively in packaging and hygiene respect.
We get the first table as follows:
In this case Ravi will get bonus of Rs 20 each from Atal, Bihari & Chirag. From Deepak he can get maximum Rs 50 as tip. So his total will not be Rs 120 therefore, this case is wrong.
Case II:- If Atal’s rank is 4th in packaging and hygiene. In this case Atal’s ratings in these two parameters will be 5 each and Deepak’s rank will be third with ratings of 7 & 6 respectively in packaging and hygiene respect.
We get the first table as follows:  In this case again he will get Rs 20 bonus from Atal, Bihari & Chirag, so his total cannot be Rs 120. Hence this case is not valid.
If we take the second case of timeliness, then the table will be
In this case again he will get Rs 20 bonus from Atal, Bihari & Chirag, so his total cannot be Rs 120. Hence this case is not valid.
If we take the second case of timeliness, then the table will be
 In this case Ravi can get tip from Atal & Deepak & will get bonus from Bihari & Chirag. Atal & Deepak can give tip of Rs 30 & Rs 50 in any order.
So he will get 120 = 20 + 20 + 30 + 50.
Bihari & Chirag gave maximum 27 points
In this case Ravi can get tip from Atal & Deepak & will get bonus from Bihari & Chirag. Atal & Deepak can give tip of Rs 30 & Rs 50 in any order.
So he will get 120 = 20 + 20 + 30 + 50.
Bihari & Chirag gave maximum 27 points
11. What rating did Atal give on Timeliness? (in numerical value)
The total tip received is Rs. 120
Now 120 = 20 + 20 + 30 + 50 or 20 + 50 + 50 + 0 or 30 + 30 + 30 + 30
It is given that in Timeliness, Ravi received a total of 21 points. As per point 1, let Atal gave x points then Bihari, Chirag and Deepak will give y each, s.t. x > y & x + 3y = 21
⇒ (x, y) are (6, 5) or (9, 4)
Total of Packaging is 29 with all distinct ratings ⇒ 29 = 9 + 8 + 7 + 5
Hygiene also has distinct ratings with a total of 26.
Now 26 = 9 + 8 + 7 + 2 or 9 + 8 + 6 + 3 or 9 + 8 + 5 + 4 or 8 + 7 + 6 + 5
Point 4 says that Chirag gave highest rating to hygiene, and also rating of Chirag as per point 3 is same for packaging & hygiene. So Chirag cannot give rating 9 to packaging as Bihari is the one giving highest rating to packaging.
∴ Chirag will give highest rating of 8 to hygiene and therefore 26 = 8 + 7 + 6 + 5
Using the point 5, the partial table can be as follows:
 Point 6 says that Atal’s Rank in Packaging & hygiene is same. So it can be rank 3 or 4 and the same is true for Deepak also.
Two cases arise here:
Case I:- If Atal’s rank is 3rd in packaging and hygiene.
In this case Atal’s rating in packaging will be 7 and in hygiene will be 6 Deepak will be ranked 4 in these parameters with ratings 5 each.
Also taking the possible values of timeliness, the table will look like as follows
Point 6 says that Atal’s Rank in Packaging & hygiene is same. So it can be rank 3 or 4 and the same is true for Deepak also.
Two cases arise here:
Case I:- If Atal’s rank is 3rd in packaging and hygiene.
In this case Atal’s rating in packaging will be 7 and in hygiene will be 6 Deepak will be ranked 4 in these parameters with ratings 5 each.
Also taking the possible values of timeliness, the table will look like as follows
 In this case Ravi will get bonus of Rs 20 each from Atal, Bihari & Chirag. From Deepak he can get maximum Rs 50 as tip. So his total will not be Rs 120 therefore, this case is wrong.
Case II:- If Atal’s rank is 4th in packaging and hygiene. In this case Atal’s ratings in these two parameters will be 5 each and Deepak’s rank will be third with ratings of 7 & 6 respectively in packaging and hygiene respect.
We get the first table as follows:
In this case Ravi will get bonus of Rs 20 each from Atal, Bihari & Chirag. From Deepak he can get maximum Rs 50 as tip. So his total will not be Rs 120 therefore, this case is wrong.
Case II:- If Atal’s rank is 4th in packaging and hygiene. In this case Atal’s ratings in these two parameters will be 5 each and Deepak’s rank will be third with ratings of 7 & 6 respectively in packaging and hygiene respect.
We get the first table as follows:
 In this case again he will get Rs 20 bonus from Atal, Bihari & Chirag, so his total cannot be Rs 120. Hence this case is not valid.
If we take the second case of timeliness, then the table will be
In this case again he will get Rs 20 bonus from Atal, Bihari & Chirag, so his total cannot be Rs 120. Hence this case is not valid.
If we take the second case of timeliness, then the table will be
 In this case Ravi can get tip from Atal & Deepak & will get bonus from Bihari & Chirag. Atal & Deepak can give tip of Rs 30 & Rs 50 in any order.
So he will get 120 = 20 + 20 + 30 + 50.
Atal gave rating of 6 on timeliness
In this case Ravi can get tip from Atal & Deepak & will get bonus from Bihari & Chirag. Atal & Deepak can give tip of Rs 30 & Rs 50 in any order.
So he will get 120 = 20 + 20 + 30 + 50.
Atal gave rating of 6 on timeliness
12. What BEST can be concluded about the tip amount given by Deepak?
- Either Rs. 0 or Rs. 30 or Rs. 50
- Rs. 50
- Either Rs. 30 or Rs. 50
- Rs. 30
The total tip received is Rs. 120
Now 120 = 20 + 20 + 30 + 50 or 20 + 50 + 50 + 0 or 30 + 30 + 30 + 30
It is given that in Timeliness, Ravi received a total of 21 points. As per point 1, let Atal gave x points then Bihari, Chirag and Deepak will give y each, s.t. x > y & x + 3y = 21
⇒ (x, y) are (6, 5) or (9, 4)
Total of Packaging is 29 with all distinct ratings ⇒ 29 = 9 + 8 + 7 + 5
Hygiene also has distinct ratings with a total of 26.
Now 26 = 9 + 8 + 7 + 2 or 9 + 8 + 6 + 3 or 9 + 8 + 5 + 4 or 8 + 7 + 6 + 5
Point 4 says that Chirag gave highest rating to hygiene, and also rating of Chirag as per point 3 is same for packaging & hygiene. So Chirag cannot give rating 9 to packaging as Bihari is the one giving highest rating to packaging.
∴ Chirag will give highest rating of 8 to hygiene and therefore 26 = 8 + 7 + 6 + 5
Using the point 5, the partial table can be as follows:
 Point 6 says that Atal’s Rank in Packaging & hygiene is same. So it can be rank 3 or 4 and the same is true for Deepak also.
Two cases arise here:
Case I:- If Atal’s rank is 3rd in packaging and hygiene.
In this case Atal’s rating in packaging will be 7 and in hygiene will be 6 Deepak will be ranked 4 in these parameters with ratings 5 each.
Also taking the possible values of timeliness, the table will look like as follows
Point 6 says that Atal’s Rank in Packaging & hygiene is same. So it can be rank 3 or 4 and the same is true for Deepak also.
Two cases arise here:
Case I:- If Atal’s rank is 3rd in packaging and hygiene.
In this case Atal’s rating in packaging will be 7 and in hygiene will be 6 Deepak will be ranked 4 in these parameters with ratings 5 each.
Also taking the possible values of timeliness, the table will look like as follows
 In this case Ravi will get bonus of Rs 20 each from Atal, Bihari & Chirag. From Deepak he can get maximum Rs 50 as tip. So his total will not be Rs 120 therefore, this case is wrong.
Case II:- If Atal’s rank is 4th in packaging and hygiene. In this case Atal’s ratings in these two parameters will be 5 each and Deepak’s rank will be third with ratings of 7 & 6 respectively in packaging and hygiene respect.
We get the first table as follows:
In this case Ravi will get bonus of Rs 20 each from Atal, Bihari & Chirag. From Deepak he can get maximum Rs 50 as tip. So his total will not be Rs 120 therefore, this case is wrong.
Case II:- If Atal’s rank is 4th in packaging and hygiene. In this case Atal’s ratings in these two parameters will be 5 each and Deepak’s rank will be third with ratings of 7 & 6 respectively in packaging and hygiene respect.
We get the first table as follows:
 In this case again he will get Rs 20 bonus from Atal, Bihari & Chirag, so his total cannot be Rs 120. Hence this case is not valid.
If we take the second case of timeliness, then the table will be
In this case again he will get Rs 20 bonus from Atal, Bihari & Chirag, so his total cannot be Rs 120. Hence this case is not valid.
If we take the second case of timeliness, then the table will be
 In this case Ravi can get tip from Atal & Deepak & will get bonus from Bihari & Chirag. Atal & Deepak can give tip of Rs 30 & Rs 50 in any order.
So he will get 120 = 20 + 20 + 30 + 50.
Deepak can give a tip of Rs 30 or 50
In this case Ravi can get tip from Atal & Deepak & will get bonus from Bihari & Chirag. Atal & Deepak can give tip of Rs 30 & Rs 50 in any order.
So he will get 120 = 20 + 20 + 30 + 50.
Deepak can give a tip of Rs 30 or 50
13. In which parameter did Atal give the maximum rating points to Ravi?
- Hygiene
- Packaging
- Timeliness
- Behaviour
The total tip received is Rs. 120
Now 120 = 20 + 20 + 30 + 50 or 20 + 50 + 50 + 0 or 30 + 30 + 30 + 30
It is given that in Timeliness, Ravi received a total of 21 points. As per point 1, let Atal gave x points then Bihari, Chirag and Deepak will give y each, s.t. x > y & x + 3y = 21
⇒ (x, y) are (6, 5) or (9, 4)
Total of Packaging is 29 with all distinct ratings ⇒ 29 = 9 + 8 + 7 + 5
Hygiene also has distinct ratings with a total of 26.
Now 26 = 9 + 8 + 7 + 2 or 9 + 8 + 6 + 3 or 9 + 8 + 5 + 4 or 8 + 7 + 6 + 5
Point 4 says that Chirag gave highest rating to hygiene, and also rating of Chirag as per point 3 is same for packaging & hygiene. So Chirag cannot give rating 9 to packaging as Bihari is the one giving highest rating to packaging.
∴ Chirag will give highest rating of 8 to hygiene and therefore 26 = 8 + 7 + 6 + 5
Using the point 5, the partial table can be as follows:
 Point 6 says that Atal’s Rank in Packaging & hygiene is same. So it can be rank 3 or 4 and the same is true for Deepak also.
Two cases arise here:
Case I:- If Atal’s rank is 3rd in packaging and hygiene.
In this case Atal’s rating in packaging will be 7 and in hygiene will be 6 Deepak will be ranked 4 in these parameters with ratings 5 each.
Also taking the possible values of timeliness, the table will look like as follows
Point 6 says that Atal’s Rank in Packaging & hygiene is same. So it can be rank 3 or 4 and the same is true for Deepak also.
Two cases arise here:
Case I:- If Atal’s rank is 3rd in packaging and hygiene.
In this case Atal’s rating in packaging will be 7 and in hygiene will be 6 Deepak will be ranked 4 in these parameters with ratings 5 each.
Also taking the possible values of timeliness, the table will look like as follows
 In this case Ravi will get bonus of Rs 20 each from Atal, Bihari & Chirag. From Deepak he can get maximum Rs 50 as tip. So his total will not be Rs 120 therefore, this case is wrong.
Case II:- If Atal’s rank is 4th in packaging and hygiene. In this case Atal’s ratings in these two parameters will be 5 each and Deepak’s rank will be third with ratings of 7 & 6 respectively in packaging and hygiene respect.
We get the first table as follows:
In this case Ravi will get bonus of Rs 20 each from Atal, Bihari & Chirag. From Deepak he can get maximum Rs 50 as tip. So his total will not be Rs 120 therefore, this case is wrong.
Case II:- If Atal’s rank is 4th in packaging and hygiene. In this case Atal’s ratings in these two parameters will be 5 each and Deepak’s rank will be third with ratings of 7 & 6 respectively in packaging and hygiene respect.
We get the first table as follows:
 In this case again he will get Rs 20 bonus from Atal, Bihari & Chirag, so his total cannot be Rs 120. Hence this case is not valid.
If we take the second case of timeliness, then the table will be
In this case again he will get Rs 20 bonus from Atal, Bihari & Chirag, so his total cannot be Rs 120. Hence this case is not valid.
If we take the second case of timeliness, then the table will be
 In this case Ravi can get tip from Atal & Deepak & will get bonus from Bihari & Chirag. Atal & Deepak can give tip of Rs 30 & Rs 50 in any order.
So he will get 120 = 20 + 20 + 30 + 50.
Atal gave maximum points in behaviour
In this case Ravi can get tip from Atal & Deepak & will get bonus from Bihari & Chirag. Atal & Deepak can give tip of Rs 30 & Rs 50 in any order.
So he will get 120 = 20 + 20 + 30 + 50.
Atal gave maximum points in behaviour
14. What rating did Deepak give on Packaging?
- 7
- 5
- 6
- 8
The total tip received is Rs. 120
Now 120 = 20 + 20 + 30 + 50 or 20 + 50 + 50 + 0 or 30 + 30 + 30 + 30
It is given that in Timeliness, Ravi received a total of 21 points. As per point 1, let Atal gave x points then Bihari, Chirag and Deepak will give y each, s.t. x > y & x + 3y = 21
⇒ (x, y) are (6, 5) or (9, 4)
Total of Packaging is 29 with all distinct ratings ⇒ 29 = 9 + 8 + 7 + 5
Hygiene also has distinct ratings with a total of 26.
Now 26 = 9 + 8 + 7 + 2 or 9 + 8 + 6 + 3 or 9 + 8 + 5 + 4 or 8 + 7 + 6 + 5
Point 4 says that Chirag gave highest rating to hygiene, and also rating of Chirag as per point 3 is same for packaging & hygiene. So Chirag cannot give rating 9 to packaging as Bihari is the one giving highest rating to packaging.
∴ Chirag will give highest rating of 8 to hygiene and therefore 26 = 8 + 7 + 6 + 5
Using the point 5, the partial table can be as follows:
 Point 6 says that Atal’s Rank in Packaging & hygiene is same. So it can be rank 3 or 4 and the same is true for Deepak also.
Two cases arise here:
Case I:- If Atal’s rank is 3rd in packaging and hygiene.
In this case Atal’s rating in packaging will be 7 and in hygiene will be 6 Deepak will be ranked 4 in these parameters with ratings 5 each.
Also taking the possible values of timeliness, the table will look like as follows
Point 6 says that Atal’s Rank in Packaging & hygiene is same. So it can be rank 3 or 4 and the same is true for Deepak also.
Two cases arise here:
Case I:- If Atal’s rank is 3rd in packaging and hygiene.
In this case Atal’s rating in packaging will be 7 and in hygiene will be 6 Deepak will be ranked 4 in these parameters with ratings 5 each.
Also taking the possible values of timeliness, the table will look like as follows
 In this case Ravi will get bonus of Rs 20 each from Atal, Bihari & Chirag. From Deepak he can get maximum Rs 50 as tip. So his total will not be Rs 120 therefore, this case is wrong.
Case II:- If Atal’s rank is 4th in packaging and hygiene. In this case Atal’s ratings in these two parameters will be 5 each and Deepak’s rank will be third with ratings of 7 & 6 respectively in packaging and hygiene respect.
We get the first table as follows:
In this case Ravi will get bonus of Rs 20 each from Atal, Bihari & Chirag. From Deepak he can get maximum Rs 50 as tip. So his total will not be Rs 120 therefore, this case is wrong.
Case II:- If Atal’s rank is 4th in packaging and hygiene. In this case Atal’s ratings in these two parameters will be 5 each and Deepak’s rank will be third with ratings of 7 & 6 respectively in packaging and hygiene respect.
We get the first table as follows:
 In this case again he will get Rs 20 bonus from Atal, Bihari & Chirag, so his total cannot be Rs 120. Hence this case is not valid.
If we take the second case of timeliness, then the table will be
In this case again he will get Rs 20 bonus from Atal, Bihari & Chirag, so his total cannot be Rs 120. Hence this case is not valid.
If we take the second case of timeliness, then the table will be
 In this case Ravi can get tip from Atal & Deepak & will get bonus from Bihari & Chirag. Atal & Deepak can give tip of Rs 30 & Rs 50 in any order.
So he will get 120 = 20 + 20 + 30 + 50.
Deepak gave rating of 7 on packaging
In this case Ravi can get tip from Atal & Deepak & will get bonus from Bihari & Chirag. Atal & Deepak can give tip of Rs 30 & Rs 50 in any order.
So he will get 120 = 20 + 20 + 30 + 50.
Deepak gave rating of 7 on packaging
Correct Answer 9
6
Correct Answer 10
Option D
Correct Answer 11
6
Correct Answer 12
Option C
Correct Answer 13
Option D
Correct Answer 14
Option A
CAT 2021 | DILR Set 4
DIRECTIONS for the question: Study the following information carefully and answer the given question.
Ten objects o1, o2, …, o10 were distributed among Amar, Barat, Charles, Disha, and Elise. Each item went to exactly one person. Each person got exactly two of the items, and this pair of objects is called her/his bundle.
The following table shows how each person values each object.
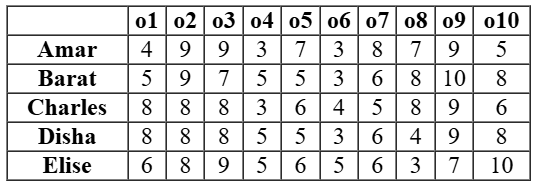
The value of any bundle by a person is the sum of that person’s values of the objects in that bundle. A person X envies another person Y if X values Y’s bundle more than X’s own bundle.
For example, hypothetically suppose Amar’s bundle consists of o1 and o2, and Barat’s bundle consists of o3 and o4. Then Amar values his own bundle at 4 + 9 = 13 and Barat’s bundle at 9 + 3 = 12. Hence Amar does not envy Barat. On the other hand, Barat values his own bundle at 7 + 5 = 12 and Amar’s bundle at 5 + 9 = 14. Hence Barat envies Amar.
The following facts are known about the actual distribution of the objects among the five people.
- If someone’s value for an object is 10, then she/he received that object.
- Objects o1, o2, and o3 were given to three different people.
- Objects o1 and o8 were given to different people.
- Three people value their own bundles at 16. No one values her/his own bundle at a number higher than 16.
- Disha values her own bundle at an odd number. All others value their own bundles at an even number.
- Some people who value their own bundles less than 16 envy some other people who value their own bundle at 16. No one else envies others.
15. What BEST can be said about object o8?
- o8 was given to Amar, Charles, or Disha
- o8 was given to Charles
- o8 was given to Disha
- o8 was given to Charles or Disha
Since, Bharat value o9 = 10 and Elsie value o10 = 10, they definitely receive so
Also, three people value their bundle = 16 and no value could be greater than 16
(Except Disha as she values her bundle as odd, number)
The other object of Bharat must be o7 = 6 to make it total = 16 (even)
And the other object of Elsie must be either o1 or o5
Now if Amar value his bundle = 16, objects received o2 or o3 = 9 and o5 or o8 = 7
Let say combination is o2 and o5, in that case Elsie must get o1
Then Charles get either o3 or o8 along with o6, total value = 12,
But Charles with those objects and score will not envy Amar as his bundle value is either equal or greater than Amar.
Likewise, in other cases as well, Charles bundle value cannot be 12
So, Charles bundle value must be = 16 and Amar bundle value must be = 12
Rest of the information can be gathered as follows
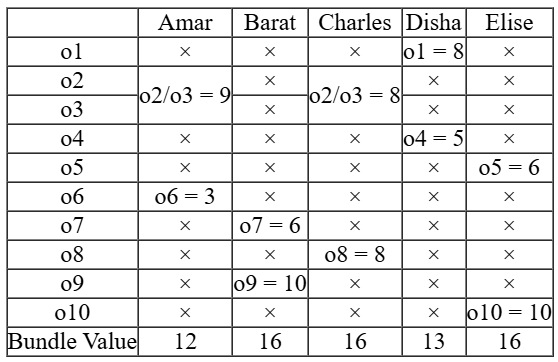 Now question can be answered using the above table
o8 was given to Charles
Now question can be answered using the above table
o8 was given to Charles
16. Who among the following envies someone else?
- Barat
- Elise
- Charles
- Amar
Since, Bharat value o9 = 10 and Elsie value o10 = 10, they definitely receive so
Also, three people value their bundle = 16 and no value could be greater than 16
(Except Disha as she values her bundle as odd, number)
The other object of Bharat must be o7 = 6 to make it total = 16 (even)
And the other object of Elsie must be either o1 or o5
Now if Amar value his bundle = 16, objects received o2 or o3 = 9 and o5 or o8 = 7
Let say combination is o2 and o5, in that case Elsie must get o1
Then Charles get either o3 or o8 along with o6, total value = 12,
But Charles with those objects and score will not envy Amar as his bundle value is either equal or greater than Amar.
Likewise, in other cases as well, Charles bundle value cannot be 12
So, Charles bundle value must be = 16 and Amar bundle value must be = 12
Rest of the information can be gathered as follows
 Now question can be answered using the above table
Amar with 12 bundle value envies others with bundle value 16
Now question can be answered using the above table
Amar with 12 bundle value envies others with bundle value 16
17. What is Amar’s value for his own bundle? (in numerical value)
Since, Bharat value o9 = 10 and Elsie value o10 = 10, they definitely receive so
Also, three people value their bundle = 16 and no value could be greater than 16
(Except Disha as she values her bundle as odd, number)
The other object of Bharat must be o7 = 6 to make it total = 16 (even)
And the other object of Elsie must be either o1 or o5
Now if Amar value his bundle = 16, objects received o2 or o3 = 9 and o5 or o8 = 7
Let say combination is o2 and o5, in that case Elsie must get o1
Then Charles get either o3 or o8 along with o6, total value = 12,
But Charles with those objects and score will not envy Amar as his bundle value is either equal or greater than Amar.
Likewise, in other cases as well, Charles bundle value cannot be 12
So, Charles bundle value must be = 16 and Amar bundle value must be = 12
Rest of the information can be gathered as follows
 Now question can be answered using the above table
Amar’s bundle value = 12
Now question can be answered using the above table
Amar’s bundle value = 12
18. Object o4 was given to
- Elise
- Charles
- Barat
- Disha
Since, Bharat value o9 = 10 and Elsie value o10 = 10, they definitely receive so
Also, three people value their bundle = 16 and no value could be greater than 16
(Except Disha as she values her bundle as odd, number)
The other object of Bharat must be o7 = 6 to make it total = 16 (even)
And the other object of Elsie must be either o1 or o5
Now if Amar value his bundle = 16, objects received o2 or o3 = 9 and o5 or o8 = 7
Let say combination is o2 and o5, in that case Elsie must get o1
Then Charles get either o3 or o8 along with o6, total value = 12,
But Charles with those objects and score will not envy Amar as his bundle value is either equal or greater than Amar.
Likewise, in other cases as well, Charles bundle value cannot be 12
So, Charles bundle value must be = 16 and Amar bundle value must be = 12
Rest of the information can be gathered as follows
 Now question can be answered using the above table
o4 was given to Disha
Now question can be answered using the above table
o4 was given to Disha
19. Object o5 was given to
- Disha
- Elise
- Charles
- Amar
Since, Bharat value o9 = 10 and Elsie value o10 = 10, they definitely receive so
Also, three people value their bundle = 16 and no value could be greater than 16
(Except Disha as she values her bundle as odd, number)
The other object of Bharat must be o7 = 6 to make it total = 16 (even)
And the other object of Elsie must be either o1 or o5
Now if Amar value his bundle = 16, objects received o2 or o3 = 9 and o5 or o8 = 7
Let say combination is o2 and o5, in that case Elsie must get o1
Then Charles get either o3 or o8 along with o6, total value = 12,
But Charles with those objects and score will not envy Amar as his bundle value is either equal or greater than Amar.
Likewise, in other cases as well, Charles bundle value cannot be 12
So, Charles bundle value must be = 16 and Amar bundle value must be = 12
Rest of the information can be gathered as follows
 Now question can be answered using the above table
o5 was given to Elise
Now question can be answered using the above table
o5 was given to Elise
20. What BEST can be said about the distribution of object o1?
- o1 was given to Charles
- o1 was given to Charles or Disha
- o1 was given to Disha
- o1 was given to Charles, Disha, or Elise
Since, Bharat value o9 = 10 and Elsie value o10 = 10, they definitely receive so
Also, three people value their bundle = 16 and no value could be greater than 16
(Except Disha as she values her bundle as odd, number)
The other object of Bharat must be o7 = 6 to make it total = 16 (even)
And the other object of Elsie must be either o1 or o5
Now if Amar value his bundle = 16, objects received o2 or o3 = 9 and o5 or o8 = 7
Let say combination is o2 and o5, in that case Elsie must get o1
Then Charles get either o3 or o8 along with o6, total value = 12,
But Charles with those objects and score will not envy Amar as his bundle value is either equal or greater than Amar.
Likewise, in other cases as well, Charles bundle value cannot be 12
So, Charles bundle value must be = 16 and Amar bundle value must be = 12
Rest of the information can be gathered as follows
 Now question can be answered using the above table
o1 was given to Disha
Now question can be answered using the above table
o1 was given to Disha
Correct Answer 15
Option B
Correct Answer 16
Option D
Correct Answer 17
12
Correct Answer 18
Option D
Correct Answer 19
Option B
Correct Answer 20
Option C