best CAT Coaching
Contact Us
Follow Us:
Flaticon-instagram Facebook-f Youtube Linkedin-in
best CAT Coaching
Step-by-Step Learning for CAT 2022

CAT 2022 DILR - Slot 2 Past Year Questions

Take Test

CAT 2022 | DILR Set 1

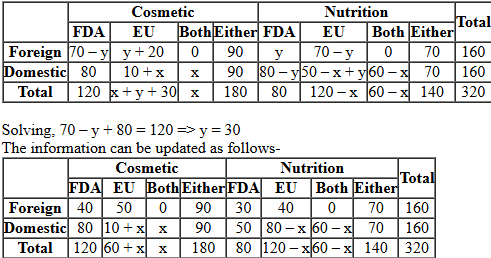
A speciality supermarket sells 320 products. Each of these products was either a cosmetic product or a nutrition product. Each of these products was also either a foreign product or a domestic product. Each of these products had at least one of the two approvals – FDA or EU.

The following facts are also known:

    1. There were equal numbers of domestic and foreign products.
    2. Half of the domestic products were FDA approved cosmetic products.
    3. None of the foreign products had both the approvals, while 60 domestic products had both the approvals.
    4. There were 140 nutrition products, half of them were foreign products.
    5. There were 200 FDA approved products. 70 of them were foreign products and 120 of them were cosmetic products

1. How many foreign products were FDA approved cosmetic products? (in numerical value only)

Total number of domestic products = foreign products = 320/2 = 160 Domestic, Cosmetic, FDA approved products = 160/2 = 80 Foreign products having both approvals = 0 Domestic products having both approvals = 60 Let the number of domestic, cosmetic, both the approvals = x => the number of domestic, nutrition, both the approvals = 60 – x Total number of nutrition products = 140 => total number of cosmetic products = 320 – 140 = 180 Number of foreign, nutrition products = 70 Let number of foreign, nutrition, FDA products = y => number of foreign, nutrition, EU products = 70 – y Also, number of foreign, cosmetic products = 160 – 70 = 90 Total FDA approved products = 200 Total foreign, FDA approved products = 70 Number of foreign, nutrition, FDA products = y => number of foreign, cosmetic, FDA products = 70 – y => number of foreign, cosmetic, EU products = 90 – (70 – y) = y + 20 Number of cosmetic, FDA approved products = 120 => number of nutrition, FDA approved products = 200 – 120 = 80 => number of domestic, nutrition, FDA approved products = 80 – y The rest of the given information can be gathered as follows- CAT 2022 DILR Slot 2 Answer Set 1 Now we can answer the questions The number of foreign products that were FDA approved cosmetic products = 40

2. How many cosmetic products did not have FDA approval?

  1. Cannot be determined
  2. 10
  3. 60
  4. 50

Total number of domestic products = foreign products = 320/2 = 160 Domestic, Cosmetic, FDA approved products = 160/2 = 80 Foreign products having both approvals = 0 Domestic products having both approvals = 60 Let the number of domestic, cosmetic, both the approvals = x => the number of domestic, nutrition, both the approvals = 60 – x Total number of nutrition products = 140 => total number of cosmetic products = 320 – 140 = 180 Number of foreign, nutrition products = 70 Let number of foreign, nutrition, FDA products = y => number of foreign, nutrition, EU products = 70 – y Also, number of foreign, cosmetic products = 160 – 70 = 90 Total FDA approved products = 200 Total foreign, FDA approved products = 70 Number of foreign, nutrition, FDA products = y => number of foreign, cosmetic, FDA products = 70 – y => number of foreign, cosmetic, EU products = 90 – (70 – y) = y + 20 Number of cosmetic, FDA approved products = 120 => number of nutrition, FDA approved products = 200 – 120 = 80 => number of domestic, nutrition, FDA approved products = 80 – y The rest of the given information can be gathered as follows- CAT 2022 DILR Slot 2 Answer Set 1 Now we can answer the questions The number of cosmetic products which have FDA approval = 120 The number of cosmetic products which did not have FDA approval = 180 – 120 = 60

3. Which among the following options best represents the number of domestic cosmetic products that had both the approvals?

  1. At least 10 and at most 60
  2. At least 10 and at most 80
  3. At least 20 and at most 50
  4. At least 20 and at most 70

Total number of domestic products = foreign products = 320/2 = 160 Domestic, Cosmetic, FDA approved products = 160/2 = 80 Foreign products having both approvals = 0 Domestic products having both approvals = 60 Let the number of domestic, cosmetic, both the approvals = x => the number of domestic, nutrition, both the approvals = 60 – x Total number of nutrition products = 140 => total number of cosmetic products = 320 – 140 = 180 Number of foreign, nutrition products = 70 Let number of foreign, nutrition, FDA products = y => number of foreign, nutrition, EU products = 70 – y Also, number of foreign, cosmetic products = 160 – 70 = 90 Total FDA approved products = 200 Total foreign, FDA approved products = 70 Number of foreign, nutrition, FDA products = y => number of foreign, cosmetic, FDA products = 70 – y => number of foreign, cosmetic, EU products = 90 – (70 – y) = y + 20 Number of cosmetic, FDA approved products = 120 => number of nutrition, FDA approved products = 200 – 120 = 80 => number of domestic, nutrition, FDA approved products = 80 – y The rest of the given information can be gathered as follows- CAT 2022 DILR Slot 2 Answer Set 1 Now we can answer the questions No value of region can be negative => 60 – x ≥ 0 => x ≤ 60 The number of domestic, cosmetic products that had both the approvals = x is at most 60 Hence, the best represents is at least 10 and at most 60

4. If 70 cosmetic products did not have EU approval, then how many nutrition products had both the approvals?

  1. 10
  2. 50
  3. 20
  4. 30

Total number of domestic products = foreign products = 320/2 = 160 Domestic, Cosmetic, FDA approved products = 160/2 = 80 Foreign products having both approvals = 0 Domestic products having both approvals = 60 Let the number of domestic, cosmetic, both the approvals = x => the number of domestic, nutrition, both the approvals = 60 – x Total number of nutrition products = 140 => total number of cosmetic products = 320 – 140 = 180 Number of foreign, nutrition products = 70 Let number of foreign, nutrition, FDA products = y => number of foreign, nutrition, EU products = 70 – y Also, number of foreign, cosmetic products = 160 – 70 = 90 Total FDA approved products = 200 Total foreign, FDA approved products = 70 Number of foreign, nutrition, FDA products = y => number of foreign, cosmetic, FDA products = 70 – y => number of foreign, cosmetic, EU products = 90 – (70 – y) = y + 20 Number of cosmetic, FDA approved products = 120 => number of nutrition, FDA approved products = 200 – 120 = 80 => number of domestic, nutrition, FDA approved products = 80 – y The rest of the given information can be gathered as follows- CAT 2022 DILR Slot 2 Answer Set 1 Now we can answer the questions The number of cosmetic products that did not have EU approval = 70 => 180 – (60 + x) = 70 => x = 50 The number of nutrition products that had both the approvals = 60 – x = 10

5. If 50 nutrition products did not have EU approval, then how many domestic cosmetic products did not have EU approval? (in numerical value only)

Total number of domestic products = foreign products = 320/2 = 160 Domestic, Cosmetic, FDA approved products = 160/2 = 80 Foreign products having both approvals = 0 Domestic products having both approvals = 60 Let the number of domestic, cosmetic, both the approvals = x => the number of domestic, nutrition, both the approvals = 60 – x Total number of nutrition products = 140 => total number of cosmetic products = 320 – 140 = 180 Number of foreign, nutrition products = 70 Let number of foreign, nutrition, FDA products = y => number of foreign, nutrition, EU products = 70 – y Also, number of foreign, cosmetic products = 160 – 70 = 90 Total FDA approved products = 200 Total foreign, FDA approved products = 70 Number of foreign, nutrition, FDA products = y => number of foreign, cosmetic, FDA products = 70 – y => number of foreign, cosmetic, EU products = 90 – (70 – y) = y + 20 Number of cosmetic, FDA approved products = 120 => number of nutrition, FDA approved products = 200 – 120 = 80 => number of domestic, nutrition, FDA approved products = 80 – y The rest of the given information can be gathered as follows- CAT 2022 DILR Slot 2 Answer Set 1 Now we can answer the questions The number of nutrition products that did not have EU approval = 50 => 140 – (120 – x) = 50 => x = 30 The number of domestic, cosmetic products that did not have EU approval = 90 – (10 + x) = 50

Correct Answer 1

40

Correct Answer 2

Option C

Correct Answer 3

Option A

Correct Answer 4

Option A

Correct Answer 5

50
Video Explanation

CAT 2022 | DILR Set 2

DIRECTIONS for the question: Read the information given below and answer the question that follows.

Every day a widget supplier supplies widgets from the warehouse (W) to four locations – Ahmednagar (A), Bikrampore (B), Chitrachak (C), and Deccan Park (D). The daily demand for widgets in each location is uncertain and independent of each other. Demands and corresponding probability values (in parenthesis) are given against each location (A, B, C, and D) in the figure below. For example, there is a 40% chance that the demand in Ahmednagar will be 50 units and a 60% chance that the demand will be 70 units. The lines in the figure connecting the locations and warehouse represent two-way roads connecting those places with the distances (in km) shown beside the line. The distances in both the directions along a road are equal. For example, the road from Ahmednagar to Bikrampore and the road from Bikrampore to Ahmednagar are both 6 km long.

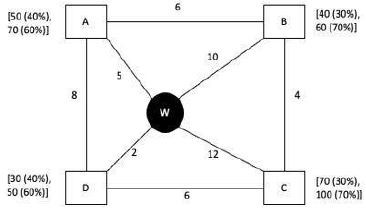
CAT 2022 DILR Slot 2 Set 2

Every day the supplier gets the information about the demand values of the four locations and creates the travel route that starts from the warehouse and ends at a location after visiting all the locations exactly once. While making the route plan, the supplier goes to the locations in decreasing order of demand. If there is a tie for the choice of the next location, the supplier will go to the location closest to the current location. Also, while creating the route, the supplier can either follow the direct path (if available) from one location to another or can take the path via the warehouse. If both paths are available (direct and via warehouse), the supplier will choose the path with minimum distance.

6. If the last location visited is Ahmednagar, then what is the total distance covered in the route (in km)? (in numerical value only)

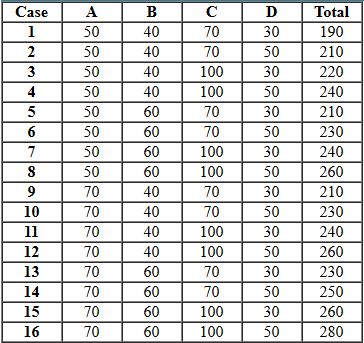CAT 2022 DILR Slot 2 Answer Set 2While making the route plan, the supplier goes to the locations in decreasing order of demand and if the last location is Ahmednagar, then it must have least demand (50 units) So, the supplier must have supplied the order in the following manner- C (70 or 100 units) > B (60 units) > D (50 units) ≥ A (50 units) The total distance (minimum) covered W – C – B – W – D – W – A = 12 + 4 + 10 + 2 + 2 + 5 = 35 km

7. If the total number of widgets delivered in a day is 250 units, then what is the total distance covered in the route (in km)? (in numerical value only)

CAT 2022 DILR Slot 2 Answer Set 2The total number of widgets delivered in a day = 250 units Only possible combination, A (70 units) + B (60 units) + C (70 units) + D (50 units) = 250 units Order of delivery, A (70 units) ≥ C (70 units) > B (60 units) > D (50 units) The total distance (minimum) covered W – A – W – C – B –W – D = 5 + 5 + 12 + 4 + 10 + 2 = 38 km

8. What is the chance that the total number of widgets delivered in a day is 260 units and the route ends at Bikrampore?

  1. 80%
  2. 64%
  3. 33%
  4. 56%

CAT 2022 DILR Slot 2 Answer Set 2The total number of widgets delivered in a day = 260 units Also, the route ends at Bikrampore, only order possible C (100 units) > A (70 units) > D (50 units) > B (40 units) Required chance = 70% × 60% × 60% × 30% = 7.56%

9. If the first location visited from the warehouse is Ahmednagar, then what is the chance that the total distance covered in the route is 40 km?

  1. 24%
  2. 30%
  3. 18%
  4. 4%

CAT 2022 DILR Slot 2 Answer Set 2CAT 2022 DILR Slot 2 Answer 9

10. If Ahmednagar is not the first location to be visited in a route and the total route distance is 29 km, then which of the following is a possible number of widgets delivered on that day?

  1. 220
  2. 210
  3. 200
  4. 250

CAT 2022 DILR Slot 2 Answer Set 2CAT 2022 DILR Slot 2 Answer 10.1 CAT 2022 DILR Slot 2 Answer 10.2

Correct Answer 6

35

Correct Answer 7

38

Correct Answer 8

Option D

Correct Answer 9

Option C

Correct Answer 10

Option B
Video Explanation

CAT 2022 | DILR Set 3

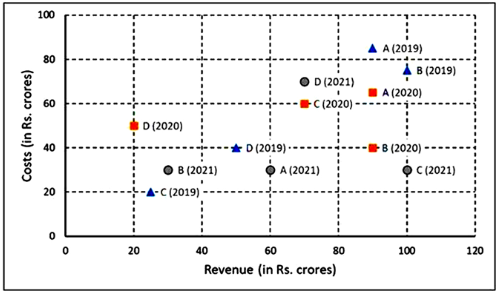
The two plots below show data for four companies code-named A, B, C, and D over three years – 2019, 2020, and 2021.

The first plot shows the revenues and costs incurred by the companies during these years. For example, in 2021, company C earned Rs.100 crores in revenue and spent Rs.30 crores. The profit of a company is defined as its revenue minus its costs.

CAT 2022 DILR Slot 2 Set 3.1

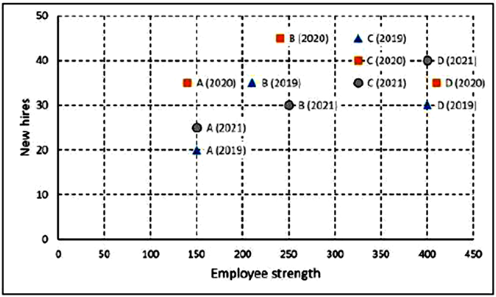
The second plot shows the number of employees employed by the company (employee strength) at the start of each of these three years, as well as the number of new employees hired each year (new hires). For example, Company B had 250 employees at the start of 2021, and 30 new employees joined the company during the year.

CAT 2022 DILR Slot 2 Set 3.2

11. Considering all three years, which company had the highest annual profit?

  1. Company B
  2. Company C
  3. Company A
  4. Company D

CAT 2022 DILR Slot 2 Answer 11

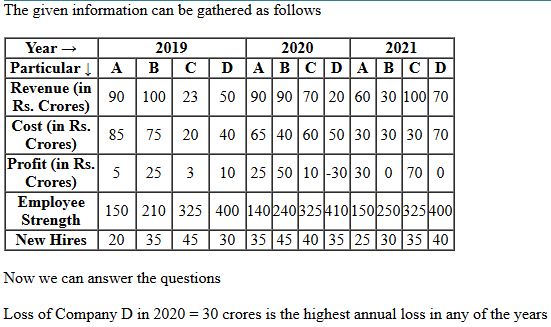
12. Which of the four companies experienced the highest annual loss in any of the years?

  1. Company A
  2. Company C
  3. Company D
  4. Company B

CAT 2022 DILR Slot 2 Answer 12

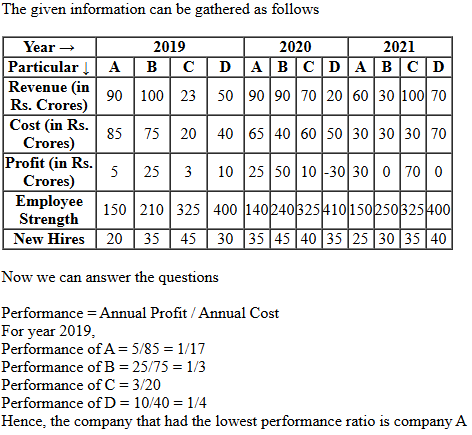
13. The ratio of a company's annual profit to its annual costs is a measure of its performance. Which of the four companies had the lowest value of this ratio in 2019?

  1. Company A
  2. Company B
  3. Company D
  4. Company C

CAT 2022 DILR Slot 2 Answer 13

14. The total number of employees lost in 2019 and 2020 was the least for:

  1. Company C
  2. Company B
  3. Company A
  4. Company D

CAT 2022 DILR Slot 2 Answer 14

15. Profit per employee is the ratio of a company's profit to its employee strength. For this purpose, the employee strength in a year is the average of the employee strength at the beginning of that year and the beginning of the next year. In 2020, which of the four companies had the highest profit per employee?

  1. Company C
  2. Company B
  3. Company A
  4. Company D

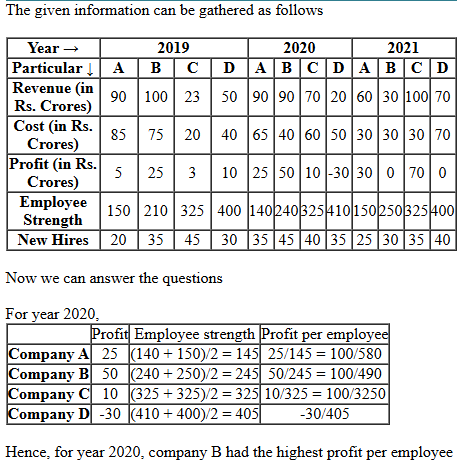
CAT 2022 DILR Slot 2 Answer 15

Correct Answer 11

Option B

Correct Answer 12

Option C

Correct Answer 13

Option A

Correct Answer 14

Option B

Correct Answer 15

Option B
Video Explanation

CAT 2022 | DILR Set 4

DIRECTIONS for the question: Read the information given below and answer the question that follows.

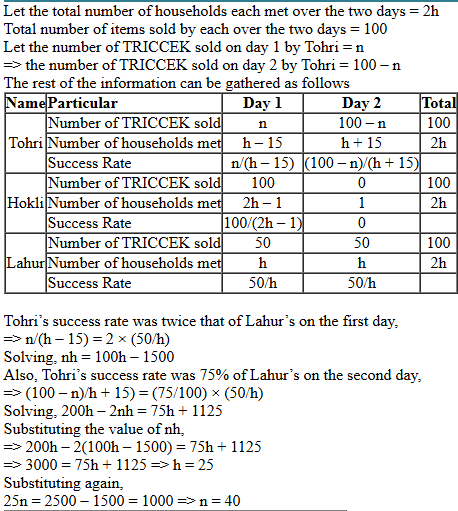
A few salesmen are employed to sell a product called TRICCEK among households in various housing complexes. On each day, a salesman is assigned to visit one housing complex. Once a salesman enters a housing complex, he can meet any number of households in the time available. However, if a household makes a complaint against the salesman, then he must leave the housing complex immediately and cannot meet any other household on that day. A household may buy any number of TRICCEK items or may not buy any item. The salesman needs to record the total number of TRICCEK items sold as well as the number of households met in each day. The success rate of a salesman for a day is defined as the ratio of the number of items sold to the number of households met on that day. Some details about the performances of three salesmen – Tohri, Hokli and Lahur, on two particular days are given below.

    1. Over the two days, all three of them met the same total number of households, and each of them sold a total of 100 items.
    2. On both days, Lahur met the same number of households and sold the same number of items.
    3. Hokli could not sell any item on the second day because the first household he met on that day complained against him.
    4. Tohri met 30 more households on the second day than on the first day.
    5. Tohri’s success rate was twice that of Lahur’s on the first day, and it was 75% of Lahur’s on the second day.

16. What was the total number of households met by Tohri, Hokli and Lahur on the first day? (in numerical value)

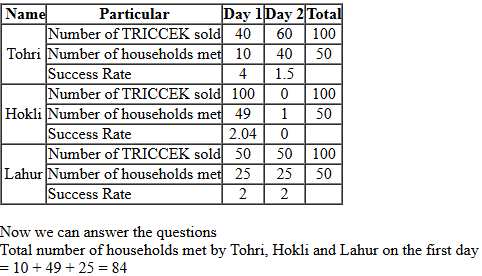
CAT 2022 DILR Slot 2 Answer 16.1 CAT 2022 DILR Slot 2 Answer 16.2

17. How many TRICCEK items were sold by Tohri on the first day? (in numerical value only)

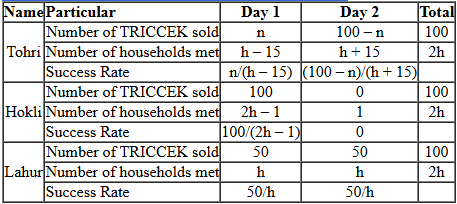
Let the total number of households each met over the two days = 2h Total number of items sold by each over the two days = 100 Let the number of TRICCEK sold on day 1 by Tohri = n => the number of TRICCEK sold on day 2 by Tohri = 100 – n The rest of the information can be gathered as follows CAT 2022 DILR Slot 2 Answer Set 4.1 Tohri’s success rate was twice that of Lahur’s on the first day, => n/(h – 15) = 2 × (50/h) Solving, nh = 100h – 1500 Also, Tohri’s success rate was 75% of Lahur’s on the second day, => (100 – n)/h + 15) = (75/100) × (50/h) Solving, 200h – 2nh = 75h + 1125 Substituting the value of nh, => 200h – 2(100h – 1500) = 75h + 1125 => 3000 = 75h + 1125 => h = 25 Substituting again, 25n = 2500 – 1500 = 1000 => n = 40 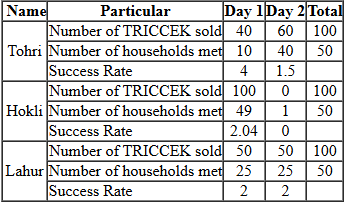CAT 2022 DILR Slot 2 Answer Set 4.2 Now we can answer the questions The number of TRICCEK items sold by Tohri on the first day = 40

18. How many households did Lahur meet on the second day?

  1. 20 or less
  2. Between 21 and 29
  3. More than 35
  4. Between 30 and 35

Let the total number of households each met over the two days = 2h Total number of items sold by each over the two days = 100 Let the number of TRICCEK sold on day 1 by Tohri = n => the number of TRICCEK sold on day 2 by Tohri = 100 – n The rest of the information can be gathered as follows CAT 2022 DILR Slot 2 Answer Set 4.1 Tohri’s success rate was twice that of Lahur’s on the first day, => n/(h – 15) = 2 × (50/h) Solving, nh = 100h – 1500 Also, Tohri’s success rate was 75% of Lahur’s on the second day, => (100 – n)/h + 15) = (75/100) × (50/h) Solving, 200h – 2nh = 75h + 1125 Substituting the value of nh, => 200h – 2(100h – 1500) = 75h + 1125 => 3000 = 75h + 1125 => h = 25 Substituting again, 25n = 2500 – 1500 = 1000 => n = 40 CAT 2022 DILR Slot 2 Answer Set 4.2 Now we can answer the questions The number of households Lahur met on the second day = 25 Hence, between 21 and 29

19. How many households did Tohri meet on the first day?

  1. Between 21 and 40
  2. 10 or less
  3. More than 40
  4. Between 11 and 20

Let the total number of households each met over the two days = 2h Total number of items sold by each over the two days = 100 Let the number of TRICCEK sold on day 1 by Tohri = n => the number of TRICCEK sold on day 2 by Tohri = 100 – n The rest of the information can be gathered as follows CAT 2022 DILR Slot 2 Answer Set 4.1 Tohri’s success rate was twice that of Lahur’s on the first day, => n/(h – 15) = 2 × (50/h) Solving, nh = 100h – 1500 Also, Tohri’s success rate was 75% of Lahur’s on the second day, => (100 – n)/h + 15) = (75/100) × (50/h) Solving, 200h – 2nh = 75h + 1125 Substituting the value of nh, => 200h – 2(100h – 1500) = 75h + 1125 => 3000 = 75h + 1125 => h = 25 Substituting again, 25n = 2500 – 1500 = 1000 => n = 40 CAT 2022 DILR Slot 2 Answer Set 4.2 Now we can answer the questions The number of households Tohri met on the first day = 10 Hence, 10 or less

20. Which of the following statements is FALSE?

  1. Among the three, Tohri had the highest success rate on the second day.
  2. Tohri had a higher success rate on the first day compared to the second day.
  3. Among the three, Tohri had the highest success rate on the first day.
  4. Among the three, Lahur had the lowest success rate on the first day.

Let the total number of households each met over the two days = 2h Total number of items sold by each over the two days = 100 Let the number of TRICCEK sold on day 1 by Tohri = n => the number of TRICCEK sold on day 2 by Tohri = 100 – n The rest of the information can be gathered as follows CAT 2022 DILR Slot 2 Answer Set 4.1 Tohri’s success rate was twice that of Lahur’s on the first day, => n/(h – 15) = 2 × (50/h) Solving, nh = 100h – 1500 Also, Tohri’s success rate was 75% of Lahur’s on the second day, => (100 – n)/h + 15) = (75/100) × (50/h) Solving, 200h – 2nh = 75h + 1125 Substituting the value of nh, => 200h – 2(100h – 1500) = 75h + 1125 => 3000 = 75h + 1125 => h = 25 Substituting again, 25n = 2500 – 1500 = 1000 => n = 40 CAT 2022 DILR Slot 2 Answer Set 4.2 Now we can answer the questions Going by options, 1. Among the three, Tohri had the highest success rate on the second day. Lahur had the highest success rate on the second day Hence, statement 1 is false. 2. Tohri had a higher success rate on the first day compared to the second day. Statement 2 is true 3. Among the three, Tohri had the highest success rate on the first day. Statement 3 is true 4. Among the three, Lahur had the lowest success rate on the first day. Statement 4 is true

Correct Answer 16

84

Correct Answer 17

40

Correct Answer 18

Option B

Correct Answer 19

Option B

Correct Answer 20

Option A
Video Explanation
free demo for CAT 2025
Quantifiers Youtube CAT 2025
best CAT Coaching

We at Quantifiers understand and deliver on the personal attention each of our students requires. Whether it is through our pedagogy that enables non-engineers or non-math background students, our constant effort to proactively provide solutions, or our focus on our student’s goals.

Know Us

Important Links

CAT 2025 Syllabus and Exam Pattern: All you need to know

Our CAT Courses

CAT Sectional Tests

CAT Past Papers

Video Resources

Free Tests

Join Free Doubt Solving Group

Blogs

CAT 2025 Strategy for repeaters

Strategic Plan to Crack CAT 2025 – A Guide for Repeaters
CAT Strategy for 99%ile

CAT 99 Percentile Strategy for 2025: Section-Wise Scores You Need

Contact Us

© Copyright Quantifiers. All Rights Reserved.

Privacy Policy

Website by Shafali Gulati