A group of N people worked on a project. They finished 35% of the project by working 7 hours a day for 10 days. Thereafter, 10 people left the group and the remaining people finished the rest of the project in 14 days by working 10 hours a day. Then the value of N is
A donation box can receive only cheques of Rs.100, Rs.250, and Rs.500. On one good day, the donation box was found to contain exactly 100 cheques amounting to a total sum of Rs.15250. Then, the maximum possible number of cheques of Rs.500 that the donation box may have contained, is (in numerical value)
Let the number of Rs 100, Rs 250 and Rs 500 cheques be x, y and z respectively Given x + y + z = 100 => 2x + 2y + 2z = 200 and 100x + 250y + 500z = 15250 => 2x + 5y + 10z = 305 Eliminating x, we get 3y + 8z = 105 To maximise z, minimise y Taking, y = 3 and z = 12 (satisfies) No other value of z which is greater than 12 satisfies the equation Hence, the maximum possible number of cheques of Rs 500 = 12
Moody takes 30 seconds to finish riding an escalator if he walks on it at his normal speed in the same direction. He takes 20 seconds to finish riding the escalator if he walks at twice his normal speed in the same direction. If Moody decides to stand still on the escalator, then the time, in seconds, needed to finish riding the escalator is (in numerical value)
The lengths of all four sides of a quadrilateral are integer valued. If three of its sides are of length 1 cm, 2 cm and 4 cm, then the total number of possible lengths of the fourth side is
Sum of the three sides of a quadrilateral is greater than the fourth side. Therefore, let the fourth side be 1 + 2 + 4 > x or x < 7 1 + 2 + x > 4 or x > 1 Possible values of d are 2, 3, 4, 5 and 6.
Bob can finish a job in 40 days, if he works alone. Alex is twice as fast as Bob and thrice as fast as Cole in the same job. Suppose Alex and Bob work together on the first day, Bob and Cole work together on the second day, Cole and Alex work together on the third day, and then, they continue the work by repeating this three- day roster, with Alex and Bob working together on the fourth day, and so on. Then, the total number of days Alex would have worked when the job gets finished, is (in numerical value)
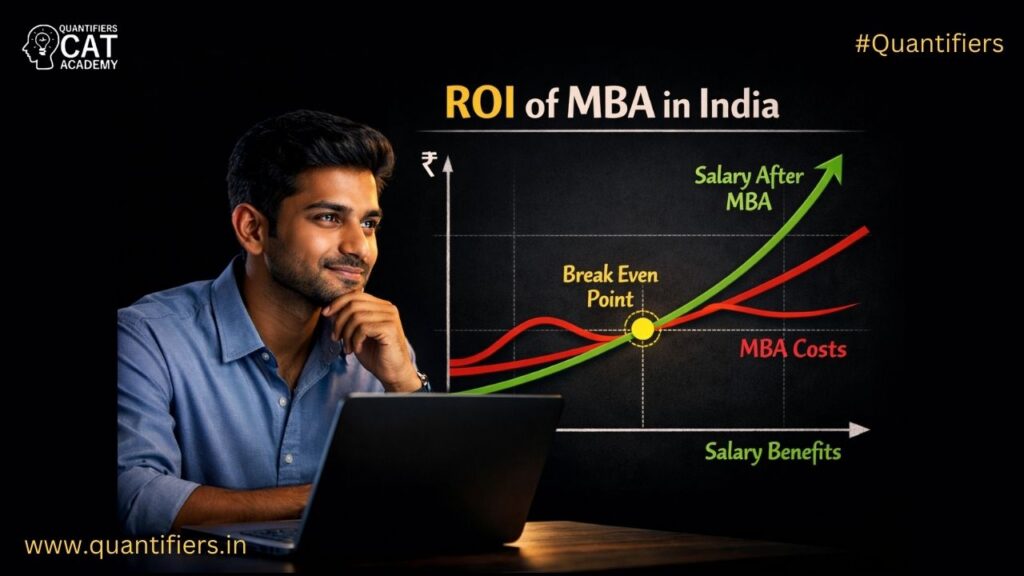
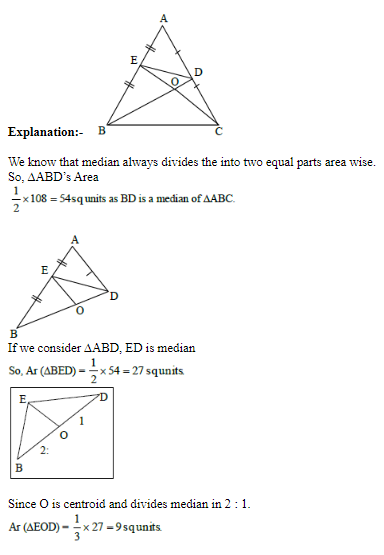
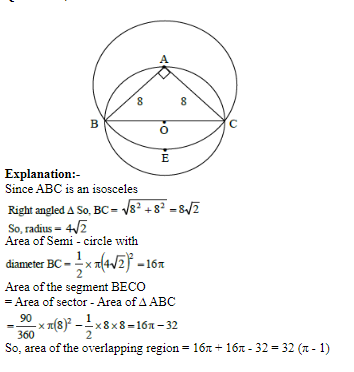
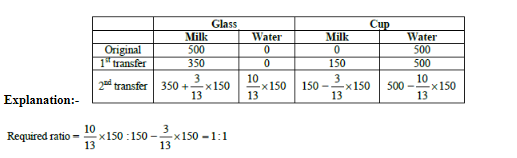
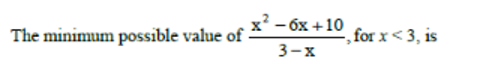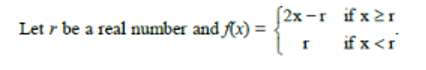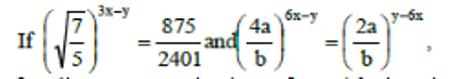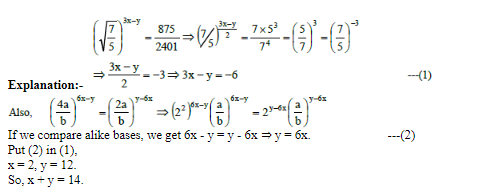B can finish job in 40 days. Since A is twice as fast as B. Since A can finish job in 20 days. Similarly C can finish job in 60 days. Let us assume total work is 120 unit So, A’s 1 day work = 6 u B’s 1 day work = 3 u C’s 1 day work = 2 u Order of their working is, AB, BC, CA, AB, BC, CA, ------------ In span of 3 days, work done = 2 (6 + 3 + 2) = 22 u. So, In span of 15 (i.e. 3 × 5) days, work done = 22 × 5 = 110 u. On 16th day, AB together will do 9 units of work. On 17th day, BC will work together to finish remaining 1 unit of work. So, in these 17 days, A will work for 2 × 5 + 1 = 11 days.
Then, the equation f(x) = f(f(x)) holds for all real values of x where.
We will go by option: Let us check at x = r f (f(x)) = f (2x - r) (by definition) = f (2x - r) = f (r) = 2x - r = r = f (x) So, f (f(x)) = f (x) when x = r So, option (3) & (4) are ruled out Now let us assume x < r f(f(x)) = f(x) (by definition) = 2r - r (Since r = r) = r = f(x) So, option (1) is answer
In a triangle ABC, AB = AC = 8cm. A circle drawn with BC as diameter passes through A. Another circle drawn with center at A passes through B and C. Then the area, in sq. cm, of the overlapping region between the two circles is
A glass contains 500 cc of milk and a cup contains 500 cc of water. From the glass, 150 cc of milk is transferred to the cup and mixed thoroughly. Next, 150 cc of this mixture is transferred from the cup to the glass. Now, the amount of water in the glass and the amount of milk in the cup are in the ratio
In an examination, the average marks of students in sections A and B are 32 and 60, respectively. The number of students in section A is 10 less than that in section B. If the average marks of all the students across both the sections combined is an integer, then the difference between the maximum and minimum possible number of students in section A is (in numerical value)
Two ships are approaching a port along straight routes at constant speeds. Initially, the two ships and the port formed an equilateral triangle with sides of length 24 km. When the slower ship travelled 8 km, the triangle formed by the new positions of the two ships and the port became right-angled. When the faster ship reaches the port, the distance, in km, between the other ship and the port will be
A school has less than 5000 students and if the students are divided equally into teams of either 9 or 10 or 12 or 25 each, exactly 4 are always left out. However, if they are divided into teams of 11 each, no one is left out. The maximum number of teams of 12 each that can be formed out of the students in the school is (in numerical value)
By looking at the first line of the question, we can say number of students should be of type 9k + 4, 10m + 4, 12l + 4, 25 s + 4 & 11 t. So, let us try to find the number which when divided by 9, 10, 12 or 25 is leaving remainder 4. i.e. number should be of type p (LCM (9, 10, 12, 25)) + 4 = 900 p + 4 = 891 p + (9p + 4) i.e. 9p + 4 should be divisible by 11. ⇒ p = 2, 13, 24, ----------------- The greatest number of student is 1804. So at the most 150 teams can be made.
Two cars travel from different locations at constant speeds. To meet each other after starting at the same time, they take 1.5 hours if they travel towards each other, but 10.5 hours if they travel in the same direction. If the speed of the slower car is 60 km/hr, then the distance traveled, in km, by the slower car when it meets the other car while traveling towards each other, is
Given speed of slower car = 60 kmph. It is given that both cars took 1.5 hours to meet if travelling towards each other. So, Required distance = 60 × 1.5 = 90 kms.
If C = 16x/y + 49y/x for some non-zero real numbers x and y, the C cannot tale te value
Given, C = 16x/y + 49y/x Let x/y = z => y/x = 1/z C = 16z + 49/z 16z2 - Cz + 40 = 0 Since, x and y are rela numbers => Disriminant ≥ 0 => C2 - 4 × 16 × 49 ≥ 0 => C2 ≥ (2 × 4 × 7)2 => C ≤ - 56 or C ≥ 56 So, - 50 is not possible
The average of all 3-digit terms in the arithmetic progression 38, 55, 72, …, is (in numerical value)
Given AP is 38, 55, 72, ... The common difference of AP = 55 - 38 = 17 The general term of the given AP = 38 + (n - 1) 17 = 17n + 21 The first 3-digit number of the AP (at n = 5) = 106 Let us find greatest 3-digit term of the given AP 999 when divided by 17 gives remainder 13 So, 986 is the greatest 3-digit number which is divisible by 17, i.e. 986 + 4 = 990 is the required number So, the required sum will be the AP 106 + 123 + … + 990 Required average = (106 + 990)/2 = 548
Nitu has an initial capital of Rs. 20,000. Out of this, she invests Rs. 8,000 at 5.5% in bank A, Rs. 5,000 at 5.6% in bank B and the remaining amount at x% in bank C, each rate being simple interest per annum. Her combined annual interest income from these investments is equal to 5% of the initial capital. If she had invested her entire initial capital in back C alone, then her annual interest income, in rupees, would have been
We at Quantifiers understand and deliver on the personal attention each of our students requires. Whether it is through our pedagogy that enables non-engineers or non-math background students, our constant effort to proactively provide solutions, or our focus on our student’s goals.
