CAT 2023 DILR - Slot 1 Past Year Questions
CAT 2023 | DILR Set 1
Direction Q.1 to 5:
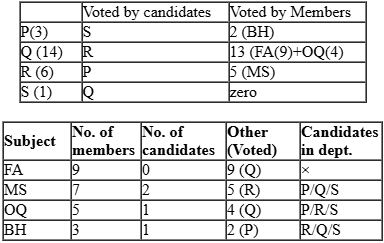
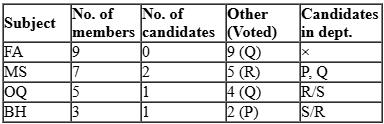
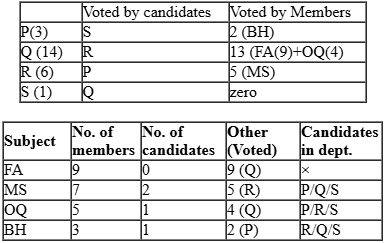
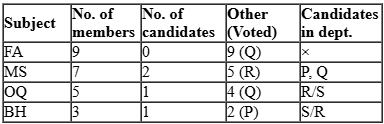
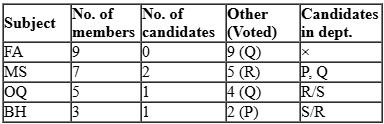
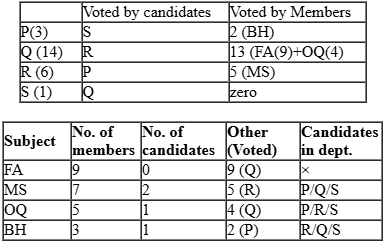
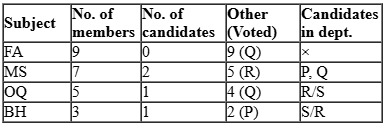
Faculty members in a management school can belong to one of four departments – Finance and Accounting (F&A), Marketing and Strategy (M&S), Operations and Quants (O&Q) and Behaviour and Human Resources (B&H). The numbers of faculty members in F&A, M&S, O&Q and B&H departments are 9, 7, 5 and 3 respectively.
Prof. Pakrasi, Prof. Qureshi, Prof. Ramaswamy and Prof. Samuel are four members of the school’s faculty who were candidates for the post of the Dean of the school. Only one of the candidates was from O&Q.
Every faculty member, including the four candidates, voted for the post. In each department, all the faculty members who were not candidates voted for the same candidate. The rules for the election are listed below.
- There cannot be more than two candidates from a single department.
- A candidate cannot vote for himself/herself.
- Faculty members cannot vote for a candidate from their own department.
After the election, it was observed that Prof. Pakrasi received 3 votes, Prof. Qureshi received 14 votes, Prof. Ramaswamy received 6 votes and Prof. Samuel received 1 vote. Prof. Pakrasi voted for Prof. Ramaswamy, Prof. Qureshi for Prof. Samuel, Prof. Ramaswamy for Prof. Qureshi and Prof. Samuel for Prof. Pakrasi.
1. Which two candidates can belong to the same department?
- Pakrasi and Prof. Samuel
- Qureshi and Prof. Ramaswamy
- Pakrasi and Prof. Qureshi
- Ramaswamy and Prof. Samuel
After reading the set, we can write following conditions.
1. There can be either 0 or 1 or 2 candidates form any department.
2. A candidate cannot vote for himself or herself.
3. Faculty members can not vote for candidate from their own department.
4. Non-candidates form same department voted for same candidate.
5. There are 9, 7, 5, 3 faculty members in FA, MS, OQ ,and BH.
6. P, Q, R, S received 3, 14, 6 and 1 votes.
7. There is exactly 1 candidate form OQ.
Since the questions are dubious, we can say there would be at least two cases.
Given Only one candidate is from OQ and there are 5 faculties from OQ ⇒ there are 4 non-candidates from OQ.
Also, P voted for R, Q for S, R for Q and S for P. Given that all non-candidates faculty members from same department voted for the same candidate. So, all 4 non-candidates from OQ can vote for candidates either Q or R.
Now P has got only 2 votes from non-candidates. From condition 4, these 2 votes can be from BH only that implies there is one candidate from BH.
R has got 5 votes which can be only from MS because of condition 4 that implies there are 2 candidates from MS.
Further, it can be determined that there is no candidates from FA. Q has got 13 non- candidates’ votes. They would be from remaining departments: FA (9) & OQ (4)
Now let us try to find which candidate is from which department.
From condition (3), R cannot be from MS. And Similarly we can determine for other candidates.
 And Q has voted for S. So, Q and S cannot be in same department. So, P is definitely one of the candidate from MS.
R has voted for Q. So, R and Q cannot be together. S has voted for P. So, P & S cannot be together. So, In MS, the candidates would be P & Q.
And Q has voted for S. So, Q and S cannot be in same department. So, P is definitely one of the candidate from MS.
R has voted for Q. So, R and Q cannot be together. S has voted for P. So, P & S cannot be together. So, In MS, the candidates would be P & Q.
 P & Q are from same department.
P & Q are from same department.
2. Which of the following can be the number of votes that Prof. Qureshi received from a single department?
- 7
- 9
- 6
- 8
After reading the set, we can write following conditions.
1. There can be either 0 or 1 or 2 candidates form any department.
2. A candidate cannot vote for himself or herself.
3. Faculty members can not vote for candidate from their own department.
4. Non-candidates form same department voted for same candidate.
5. There are 9, 7, 5, 3 faculty members in FA, MS, OQ ,and BH.
6. P, Q, R, S received 3, 14, 6 and 1 votes.
7. There is exactly 1 candidate form OQ.
Since the questions are dubious, we can say there would be at least two cases.
Given Only one candidate is from OQ and there are 5 faculties from OQ ⇒ there are 4 non-candidates from OQ.
Also, P voted for R, Q for S, R for Q and S for P. Given that all non-candidates faculty members from same department voted for the same candidate. So, all 4 non-candidates from OQ can vote for candidates either Q or R.
Now P has got only 2 votes from non-candidates. From condition 4, these 2 votes can be from BH only that implies there is one candidate from BH.
R has got 5 votes which can be only from MS because of condition 4 that implies there are 2 candidates from MS.
Further, it can be determined that there is no candidates from FA. Q has got 13 non- candidates’ votes. They would be from remaining departments: FA (9) & OQ (4)
Now let us try to find which candidate is from which department.
From condition (3), R cannot be from MS. And Similarly we can determine for other candidates.
 And Q has voted for S. So, Q and S cannot be in same department. So, P is definitely one of the candidate from MS.
R has voted for Q. So, R and Q cannot be together. S has voted for P. So, P & S cannot be together. So, In MS, the candidates would be P & Q.
And Q has voted for S. So, Q and S cannot be in same department. So, P is definitely one of the candidate from MS.
R has voted for Q. So, R and Q cannot be together. S has voted for P. So, P & S cannot be together. So, In MS, the candidates would be P & Q.
 Q gets 9 from FA and 4 from OQ. So, answer is 9.
Q gets 9 from FA and 4 from OQ. So, answer is 9.
3. If Prof. Samuel belongs to B&H, which of the following statements is/are true? Statement A: Prof. Pakrasi belongs to M&S. Statement B: Prof. Ramaswamy belongs to O&Q.
- Only statement A
- Only statement B
- Neither statement A nor statement B
- Both statements A and B
After reading the set, we can write following conditions.
1. There can be either 0 or 1 or 2 candidates form any department.
2. A candidate cannot vote for himself or herself.
3. Faculty members can not vote for candidate from their own department.
4. Non-candidates form same department voted for same candidate.
5. There are 9, 7, 5, 3 faculty members in FA, MS, OQ ,and BH.
6. P, Q, R, S received 3, 14, 6 and 1 votes.
7. There is exactly 1 candidate form OQ.
Since the questions are dubious, we can say there would be at least two cases.
Given Only one candidate is from OQ and there are 5 faculties from OQ ⇒ there are 4 non-candidates from OQ.
Also, P voted for R, Q for S, R for Q and S for P. Given that all non-candidates faculty members from same department voted for the same candidate. So, all 4 non-candidates from OQ can vote for candidates either Q or R.
Now P has got only 2 votes from non-candidates. From condition 4, these 2 votes can be from BH only that implies there is one candidate from BH.
R has got 5 votes which can be only from MS because of condition 4 that implies there are 2 candidates from MS.
Further, it can be determined that there is no candidates from FA. Q has got 13 non- candidates’ votes. They would be from remaining departments: FA (9) & OQ (4)
Now let us try to find which candidate is from which department.
From condition (3), R cannot be from MS. And Similarly we can determine for other candidates.
 And Q has voted for S. So, Q and S cannot be in same department. So, P is definitely one of the candidate from MS.
R has voted for Q. So, R and Q cannot be together. S has voted for P. So, P & S cannot be together. So, In MS, the candidates would be P & Q.
And Q has voted for S. So, Q and S cannot be in same department. So, P is definitely one of the candidate from MS.
R has voted for Q. So, R and Q cannot be together. S has voted for P. So, P & S cannot be together. So, In MS, the candidates would be P & Q.
 Both statements are true.
Both statements are true.
4. What best can be concluded about the candidate from O&Q?
- It was Prof. Ramaswamy.
- It was Prof. Samuel.
- It was either Prof. Pakrasi or Prof. Qureshi.
- It was either Prof. Ramaswamy or Prof. Samuel.
After reading the set, we can write following conditions.
1. There can be either 0 or 1 or 2 candidates form any department.
2. A candidate cannot vote for himself or herself.
3. Faculty members can not vote for candidate from their own department.
4. Non-candidates form same department voted for same candidate.
5. There are 9, 7, 5, 3 faculty members in FA, MS, OQ ,and BH.
6. P, Q, R, S received 3, 14, 6 and 1 votes.
7. There is exactly 1 candidate form OQ.
Since the questions are dubious, we can say there would be at least two cases.
Given Only one candidate is from OQ and there are 5 faculties from OQ ⇒ there are 4 non-candidates from OQ.
Also, P voted for R, Q for S, R for Q and S for P. Given that all non-candidates faculty members from same department voted for the same candidate. So, all 4 non-candidates from OQ can vote for candidates either Q or R.
Now P has got only 2 votes from non-candidates. From condition 4, these 2 votes can be from BH only that implies there is one candidate from BH.
R has got 5 votes which can be only from MS because of condition 4 that implies there are 2 candidates from MS.
Further, it can be determined that there is no candidates from FA. Q has got 13 non- candidates’ votes. They would be from remaining departments: FA (9) & OQ (4)
Now let us try to find which candidate is from which department.
From condition (3), R cannot be from MS. And Similarly we can determine for other candidates.
 And Q has voted for S. So, Q and S cannot be in same department. So, P is definitely one of the candidate from MS.
R has voted for Q. So, R and Q cannot be together. S has voted for P. So, P & S cannot be together. So, In MS, the candidates would be P & Q.
And Q has voted for S. So, Q and S cannot be in same department. So, P is definitely one of the candidate from MS.
R has voted for Q. So, R and Q cannot be together. S has voted for P. So, P & S cannot be together. So, In MS, the candidates would be P & Q.
 It was either Prof. Ramaswamy or Prof. Samuel.
It was either Prof. Ramaswamy or Prof. Samuel.
5. Which of the following statements is/are true? Statement A: Non-candidates from M&S voted for Prof. Qureshi. Statement B: Non-candidates from F&A voted for Prof. Qureshi.
- Both statements A and B
- Only statement B
- Neither statement A nor statement B
- Only statement A
After reading the set, we can write following conditions.
1. There can be either 0 or 1 or 2 candidates form any department.
2. A candidate cannot vote for himself or herself.
3. Faculty members can not vote for candidate from their own department.
4. Non-candidates form same department voted for same candidate.
5. There are 9, 7, 5, 3 faculty members in FA, MS, OQ ,and BH.
6. P, Q, R, S received 3, 14, 6 and 1 votes.
7. There is exactly 1 candidate form OQ.
Since the questions are dubious, we can say there would be at least two cases.
Given Only one candidate is from OQ and there are 5 faculties from OQ ⇒ there are 4 non-candidates from OQ.
Also, P voted for R, Q for S, R for Q and S for P. Given that all non-candidates faculty members from same department voted for the same candidate. So, all 4 non-candidates from OQ can vote for candidates either Q or R.
Now P has got only 2 votes from non-candidates. From condition 4, these 2 votes can be from BH only that implies there is one candidate from BH.
R has got 5 votes which can be only from MS because of condition 4 that implies there are 2 candidates from MS.
Further, it can be determined that there is no candidates from FA. Q has got 13 non- candidates’ votes. They would be from remaining departments: FA (9) & OQ (4)
Now let us try to find which candidate is from which department.
From condition (3), R cannot be from MS. And Similarly we can determine for other candidates.
 And Q has voted for S. So, Q and S cannot be in same department. So, P is definitely one of the candidate from MS.
R has voted for Q. So, R and Q cannot be together. S has voted for P. So, P & S cannot be together. So, In MS, the candidates would be P & Q.
And Q has voted for S. So, Q and S cannot be in same department. So, P is definitely one of the candidate from MS.
R has voted for Q. So, R and Q cannot be together. S has voted for P. So, P & S cannot be together. So, In MS, the candidates would be P & Q.
 Only statement (B) is true.
Only statement (B) is true.
Correct Answer 1
Option 3
Correct Answer 2
Option 2
Correct Answer 3
Option 4
Correct Answer 4
Option 4
Correct Answer 5
Option 2
CAT 2023 | DILR Set 2
Direction Q.6 to 10:
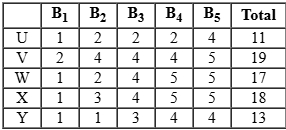
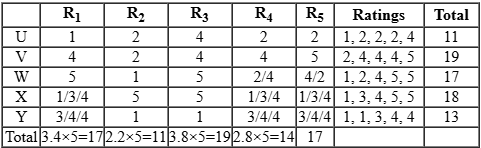
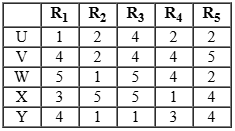
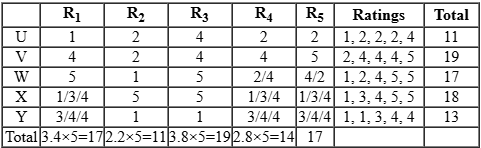
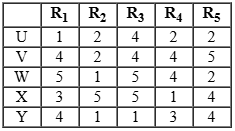
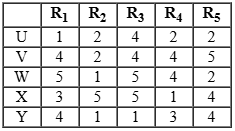
Five restaurants, coded R1, R2, R3, R4 and R5 gave integer ratings to five gig workers – Ullas, Vasu, Waman, Xavier and Yusuf, on a scale of 1 to 5.
The means of the ratings given by R1, R2, R3, R4 and R5 were 3.4, 2.2, 3.8, 2.8 and 3.4 respectively.
The summary statistics of these ratings for the five workers is given below.
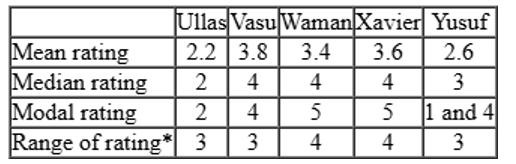
*Range of ratings is defined as the difference between the maximum and minimum ratings awarded to a worker.
The following is partial information about ratings of 1 and 5 awarded by the restaurants to the workers.
(a) R1 awarded a rating of 5 to Waman, as did R2 to Xavier, R3 to Waman and Xavier, and R5 to Vasu.
(b) R1 awarded a rating of 1 to Ullas, as did R2 to Waman and Yusuf, and R3 to Yusuf.
6. How many individual ratings cannot be determined from the above information? (in numerial value)
To solve this set, following definitions we need to know:
Mean = Sum of items/ no. of items
Median = middle value after arranging the data in either ascending or descending order.
Mode = the number which is appearing highest number of times
Range = Maximum number – Minimum number
By using Mean formula; we can calculate total of all ratings given by all restaurants to each worker.
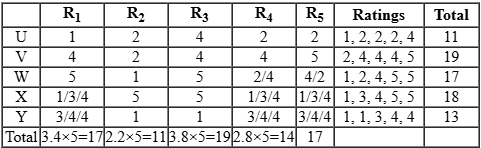
For Ullas, U = 2.2 × 5 = 11
V = 3.8 × 5 = 19
W = 3.4 × 5 = 17
X = 3.6 × 5 = 18
Y = 2.6 × 5 = 13
For Ullas, median rating is 2 i.e. middle most rating is 2. So, two lowest ratings are £ 2. Also, mode is 2. It means there should be atleast two 2’s in ratings. Range = 3. That means Max rating – Min. rating = 3. R1 awarded rating of 1 to U. Means maximum rating can be 4 only. So far we have deducted 4 ratings of U and they are are 1, 4, 2, 2. Since total is 11. So, all ratings are 1, 2, 2, 2, 4.
For V, total is 19. If we give 5 rating every time we will get total of 20. It means ratings are 2, 4, 4, 4, 5. (Because range is 3.)
For w, Similarly we can say, ratings are 1, 2, 4, 5, 5.
For x, ratings are 1, 3, 4, 5, 5.
For y, there are two modes 1 & 4. It means 1 and 4 will occur atleast twice. So, ratings are 1, 1, 3, 4, 4.
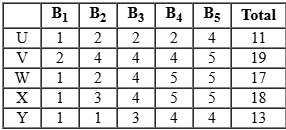
B1 < B2 < B3 < B4 < B5 where Bi = ratings i
 Now Let us try to find a link between workers and restaurants.
Now Let us try to find a link between workers and restaurants.
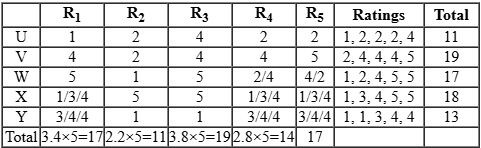 Since total of ratings given by R3 is 19. It is possible only if remaining ratings are 4 & 4. Because all 5’s are used.
Let us think, for R4;
Possible ratings are 2, 4, 2/4, 1/3/4 or 3/4/4
Total = 14
So, possible cases are 2, 4, 2, 3, 3 or 2, 4, 4, 1, 3
But by putting 2, 4, 2, 3, 3, the table is not satisfied.
So, now we can make a new table:
Since total of ratings given by R3 is 19. It is possible only if remaining ratings are 4 & 4. Because all 5’s are used.
Let us think, for R4;
Possible ratings are 2, 4, 2/4, 1/3/4 or 3/4/4
Total = 14
So, possible cases are 2, 4, 2, 3, 3 or 2, 4, 4, 1, 3
But by putting 2, 4, 2, 3, 3, the table is not satisfied.
So, now we can make a new table:
 Ans is 0
Ans is 0
7. To how many workers did R2 give a rating of 4? (in numerial value)
To solve this set, following definitions we need to know:
Mean = Sum of items/ no. of items
Median = middle value after arranging the data in either ascending or descending order.
Mode = the number which is appearing highest number of times
Range = Maximum number – Minimum number
By using Mean formula; we can calculate total of all ratings given by all restaurants to each worker.
For Ullas, U = 2.2 × 5 = 11
V = 3.8 × 5 = 19
W = 3.4 × 5 = 17
X = 3.6 × 5 = 18
Y = 2.6 × 5 = 13
For Ullas, median rating is 2 i.e. middle most rating is 2. So, two lowest ratings are £ 2. Also, mode is 2. It means there should be atleast two 2’s in ratings. Range = 3. That means Max rating – Min. rating = 3. R1 awarded rating of 1 to U. Means maximum rating can be 4 only. So far we have deducted 4 ratings of U and they are are 1, 4, 2, 2. Since total is 11. So, all ratings are 1, 2, 2, 2, 4.
For V, total is 19. If we give 5 rating every time we will get total of 20. It means ratings are 2, 4, 4, 4, 5. (Because range is 3.)
For w, Similarly we can say, ratings are 1, 2, 4, 5, 5.
For x, ratings are 1, 3, 4, 5, 5.
For y, there are two modes 1 & 4. It means 1 and 4 will occur atleast twice. So, ratings are 1, 1, 3, 4, 4.
B1 < B2 < B3 < B4 < B5 where Bi = ratings i
 Now Let us try to find a link between workers and restaurants.
Now Let us try to find a link between workers and restaurants.
 Since total of ratings given by R3 is 19. It is possible only if remaining ratings are 4 & 4. Because all 5’s are used.
Let us think, for R4;
Possible ratings are 2, 4, 2/4, 1/3/4 or 3/4/4
Total = 14
So, possible cases are 2, 4, 2, 3, 3 or 2, 4, 4, 1, 3
But by putting 2, 4, 2, 3, 3, the table is not satisfied.
So, now we can make a new table:
Since total of ratings given by R3 is 19. It is possible only if remaining ratings are 4 & 4. Because all 5’s are used.
Let us think, for R4;
Possible ratings are 2, 4, 2/4, 1/3/4 or 3/4/4
Total = 14
So, possible cases are 2, 4, 2, 3, 3 or 2, 4, 4, 1, 3
But by putting 2, 4, 2, 3, 3, the table is not satisfied.
So, now we can make a new table:
 Ans is 0
Ans is 0
8. What rating did R1 give to Xavier? (in numerial value)
To solve this set, following definitions we need to know:
Mean = Sum of items/ no. of items
Median = middle value after arranging the data in either ascending or descending order.
Mode = the number which is appearing highest number of times
Range = Maximum number – Minimum number
By using Mean formula; we can calculate total of all ratings given by all restaurants to each worker.
For Ullas, U = 2.2 × 5 = 11
V = 3.8 × 5 = 19
W = 3.4 × 5 = 17
X = 3.6 × 5 = 18
Y = 2.6 × 5 = 13
For Ullas, median rating is 2 i.e. middle most rating is 2. So, two lowest ratings are £ 2. Also, mode is 2. It means there should be atleast two 2’s in ratings. Range = 3. That means Max rating – Min. rating = 3. R1 awarded rating of 1 to U. Means maximum rating can be 4 only. So far we have deducted 4 ratings of U and they are are 1, 4, 2, 2. Since total is 11. So, all ratings are 1, 2, 2, 2, 4.
For V, total is 19. If we give 5 rating every time we will get total of 20. It means ratings are 2, 4, 4, 4, 5. (Because range is 3.)
For w, Similarly we can say, ratings are 1, 2, 4, 5, 5.
For x, ratings are 1, 3, 4, 5, 5.
For y, there are two modes 1 & 4. It means 1 and 4 will occur atleast twice. So, ratings are 1, 1, 3, 4, 4.
B1 < B2 < B3 < B4 < B5 where Bi = ratings i
 Now Let us try to find a link between workers and restaurants.
Now Let us try to find a link between workers and restaurants.
 Since total of ratings given by R3 is 19. It is possible only if remaining ratings are 4 & 4. Because all 5’s are used.
Let us think, for R4;
Possible ratings are 2, 4, 2/4, 1/3/4 or 3/4/4
Total = 14
So, possible cases are 2, 4, 2, 3, 3 or 2, 4, 4, 1, 3
But by putting 2, 4, 2, 3, 3, the table is not satisfied.
So, now we can make a new table:
Since total of ratings given by R3 is 19. It is possible only if remaining ratings are 4 & 4. Because all 5’s are used.
Let us think, for R4;
Possible ratings are 2, 4, 2/4, 1/3/4 or 3/4/4
Total = 14
So, possible cases are 2, 4, 2, 3, 3 or 2, 4, 4, 1, 3
But by putting 2, 4, 2, 3, 3, the table is not satisfied.
So, now we can make a new table:
 Ans is 3
Ans is 3
9. What is the median of the ratings given by R3 to the five workers? (in numerial value)
To solve this set, following definitions we need to know:
Mean = Sum of items/ no. of items
Median = middle value after arranging the data in either ascending or descending order.
Mode = the number which is appearing highest number of times
Range = Maximum number – Minimum number
By using Mean formula; we can calculate total of all ratings given by all restaurants to each worker.
For Ullas, U = 2.2 × 5 = 11
V = 3.8 × 5 = 19
W = 3.4 × 5 = 17
X = 3.6 × 5 = 18
Y = 2.6 × 5 = 13
For Ullas, median rating is 2 i.e. middle most rating is 2. So, two lowest ratings are £ 2. Also, mode is 2. It means there should be atleast two 2’s in ratings. Range = 3. That means Max rating – Min. rating = 3. R1 awarded rating of 1 to U. Means maximum rating can be 4 only. So far we have deducted 4 ratings of U and they are are 1, 4, 2, 2. Since total is 11. So, all ratings are 1, 2, 2, 2, 4.
For V, total is 19. If we give 5 rating every time we will get total of 20. It means ratings are 2, 4, 4, 4, 5. (Because range is 3.)
For w, Similarly we can say, ratings are 1, 2, 4, 5, 5.
For x, ratings are 1, 3, 4, 5, 5.
For y, there are two modes 1 & 4. It means 1 and 4 will occur atleast twice. So, ratings are 1, 1, 3, 4, 4.
B1 < B2 < B3 < B4 < B5 where Bi = ratings i
 Now Let us try to find a link between workers and restaurants.
Now Let us try to find a link between workers and restaurants.
 Since total of ratings given by R3 is 19. It is possible only if remaining ratings are 4 & 4. Because all 5’s are used.
Let us think, for R4;
Possible ratings are 2, 4, 2/4, 1/3/4 or 3/4/4
Total = 14
So, possible cases are 2, 4, 2, 3, 3 or 2, 4, 4, 1, 3
But by putting 2, 4, 2, 3, 3, the table is not satisfied.
So, now we can make a new table:
Since total of ratings given by R3 is 19. It is possible only if remaining ratings are 4 & 4. Because all 5’s are used.
Let us think, for R4;
Possible ratings are 2, 4, 2/4, 1/3/4 or 3/4/4
Total = 14
So, possible cases are 2, 4, 2, 3, 3 or 2, 4, 4, 1, 3
But by putting 2, 4, 2, 3, 3, the table is not satisfied.
So, now we can make a new table:
 Ratings are 1, 4, 4, 5, 5.
So, median is 4.
Ratings are 1, 4, 4, 5, 5.
So, median is 4.
10. Which among the following restaurants gave its median rating to exactly one of the workers?
- R2
- R5
- R3
- R4
To solve this set, following definitions we need to know:
Mean = Sum of items/ no. of items
Median = middle value after arranging the data in either ascending or descending order.
Mode = the number which is appearing highest number of times
Range = Maximum number – Minimum number
By using Mean formula; we can calculate total of all ratings given by all restaurants to each worker.
For Ullas, U = 2.2 × 5 = 11
V = 3.8 × 5 = 19
W = 3.4 × 5 = 17
X = 3.6 × 5 = 18
Y = 2.6 × 5 = 13
For Ullas, median rating is 2 i.e. middle most rating is 2. So, two lowest ratings are £ 2. Also, mode is 2. It means there should be atleast two 2’s in ratings. Range = 3. That means Max rating – Min. rating = 3. R1 awarded rating of 1 to U. Means maximum rating can be 4 only. So far we have deducted 4 ratings of U and they are are 1, 4, 2, 2. Since total is 11. So, all ratings are 1, 2, 2, 2, 4.
For V, total is 19. If we give 5 rating every time we will get total of 20. It means ratings are 2, 4, 4, 4, 5. (Because range is 3.)
For w, Similarly we can say, ratings are 1, 2, 4, 5, 5.
For x, ratings are 1, 3, 4, 5, 5.
For y, there are two modes 1 & 4. It means 1 and 4 will occur atleast twice. So, ratings are 1, 1, 3, 4, 4.
B1 < B2 < B3 < B4 < B5 where Bi = ratings i
 Now Let us try to find a link between workers and restaurants.
Now Let us try to find a link between workers and restaurants.
 Since total of ratings given by R3 is 19. It is possible only if remaining ratings are 4 & 4. Because all 5’s are used.
Let us think, for R4;
Possible ratings are 2, 4, 2/4, 1/3/4 or 3/4/4
Total = 14
So, possible cases are 2, 4, 2, 3, 3 or 2, 4, 4, 1, 3
But by putting 2, 4, 2, 3, 3, the table is not satisfied.
So, now we can make a new table:
Since total of ratings given by R3 is 19. It is possible only if remaining ratings are 4 & 4. Because all 5’s are used.
Let us think, for R4;
Possible ratings are 2, 4, 2/4, 1/3/4 or 3/4/4
Total = 14
So, possible cases are 2, 4, 2, 3, 3 or 2, 4, 4, 1, 3
But by putting 2, 4, 2, 3, 3, the table is not satisfied.
So, now we can make a new table:
 R1 median = 4 (given twice) (1, 3, 4, 4, 5)
R2 median = 2 (given twice) (1, 1, 2, 2, 5)
R3 median = 4 (given twice) (1, 4, 4, 5, 5)
R4 median = 3 (given once) (1, 2, 3, 4, 4)
R5 median = 4 (given twice) (2, 2, 4, 4, 5)
So, answer is R4
R1 median = 4 (given twice) (1, 3, 4, 4, 5)
R2 median = 2 (given twice) (1, 1, 2, 2, 5)
R3 median = 4 (given twice) (1, 4, 4, 5, 5)
R4 median = 3 (given once) (1, 2, 3, 4, 4)
R5 median = 4 (given twice) (2, 2, 4, 4, 5)
So, answer is R4
Correct Answer 6
0
Correct Answer 7
0
Correct Answer 8
3
Correct Answer 9
4
Correct Answer 10
Option 4
CAT 2023 | DILR Set 3
Direction Q.11 to 15:
A visa processing office (VPO) accepts visa applications in four categories – US, UK, Schengen, and Others. The applications are scheduled for processing in twenty 15-minute slots starting at 9:00 am and ending at 2:00 pm. Ten applications are scheduled in each slot.
There are ten counters in the office, four dedicated to US applications, and two each for UK applications, Schengen applications and Others applications. Applicants are called in for processing sequentially on a first-come-first-served basis whenever a counter gets freed for their category. The processing time for an application is the same within each category. But it may vary across the categories. Each US and UK application requires 10 minutes of processing time. Depending on the number of applications in a category and time required to process an application for that category, it is possible that an applicant for a slot may be processed later.
On a particular day, Ira, Vijay and Nandini were scheduled for Schengen visa processing in that order. They had a 9:15 am slot but entered the VPO at 9:20 am. When they entered the office, exactly six out of the ten counters were either processing applications, or had finished processing one and ready to start processing the next.
Mahira and Osman were scheduled in the 9:30 am slot on that day for visa processing in the Others category.
The following additional information is known about that day.
- All slots were full.
- The number of US applications was the same in all the slots. The same was true for the other three categories.
- 50% of the applications were US applications.
- All applicants except Ira, Vijay and Nandini arrived on time.
- Vijay was called to a counter at 9:25 am.
11. How many UK applications were scheduled on that day? (in numerial value)
Given slots are twenty 15 minutes slots starting at 9AM and ending at 2PM. Then applicants are scheduled in each slot. Total number of applicants = 10 × 20 = 200 No. of US applications = 50% of Total = 50% of 200 = 100 Since the number of US applications was the same in all slots. So, US applications in each slot = 100/20 = 5 It is given that I, V and N were scheduled for Schengen visa processing in that order. Their slot was 9:15 AM. It means the number of Schengen applicants in each slot is at least 3. Similarly, it is given that M and O were scheduled in the 9:30AM slot in others category. So, the number of applicants in other category in each slot is at least 2. Since the number of applicants in each slots is 10. So, it can be inferred that number of Schengen and others applicants is 3 and 2 respectively. Hence the number of UK applicants is 0 in each slot. Total number of counters = 10 US counters = 4 UK counters = 2 Schengen counters = 2 Others counters = 2 Given that US and UK application requires 10 mins of processing time. Vijay was called at 9:25 A.M. (5th in line). It is possible if processing time for Schengen visa is 12.5 mins. On a particular day, I, V and N were scheduled for Schengen visa processing in given order. They had 9:15 AM slot but entered at 9:20 A.M. when they entered VPO, exactly 6 out of 10 counters were either processing applications or had finished processing ones and ready to start processing the next. Hence at 9:20 A.M. there are exactly 4 free counters. Out of these 4 free counters, 2 would be UK and 2 would be others. So, for US (Processing time is 10 mins) slots counter-wise are, C1 : 9:10, 9:20, 9:30, 9:40, 9:55, 10:10, 10:20 C2 : 9:10, 9:25, 9:35, 9:45, 9:55, 10:10 C3 : 9:10, 9:25, 9:40, 9:50, 10:00, 10:10 C4 : 9:10, 9:25, 9:40, 9:55, 10:05, 10:15 For Schengen visa (12.5 mins) slots are C1 : 9:12.30, 9:25. 9:37.30 C2 : 9:12.30, 9:32.30, 9:45 For others (5 mins) slots are C1 → 9:05, 9:20, 9:35 C2 → 9:05, 9:20, 9:35 0 is the answer.
12. What is the maximum possible value of the total time (in minutes, nearest to its integer value) required to process all applications in the Others category on that day? (in numerial value)
Given slots are twenty 15 minutes slots starting at 9AM and ending at 2PM. Then applicants are scheduled in each slot. Total number of applicants = 10 × 20 = 200 No. of US applications = 50% of Total = 50% of 200 = 100 Since the number of US applications was the same in all slots. So, US applications in each slot = 100/20 = 5 It is given that I, V and N were scheduled for Schengen visa processing in that order. Their slot was 9:15 AM. It means the number of Schengen applicants in each slot is at least 3. Similarly, it is given that M and O were scheduled in the 9:30AM slot in others category. So, the number of applicants in other category in each slot is at least 2. Since the number of applicants in each slots is 10. So, it can be inferred that number of Schengen and others applicants is 3 and 2 respectively. Hence the number of UK applicants is 0 in each slot. Total number of counters = 10 US counters = 4 UK counters = 2 Schengen counters = 2 Others counters = 2 Given that US and UK application requires 10 mins of processing time. Vijay was called at 9:25 A.M. (5th in line). It is possible if processing time for Schengen visa is 12.5 mins. On a particular day, I, V and N were scheduled for Schengen visa processing in given order. They had 9:15 AM slot but entered at 9:20 A.M. when they entered VPO, exactly 6 out of 10 counters were either processing applications or had finished processing ones and ready to start processing the next. Hence at 9:20 A.M. there are exactly 4 free counters. Out of these 4 free counters, 2 would be UK and 2 would be others. So, for US (Processing time is 10 mins) slots counter-wise are, C1 : 9:10, 9:20, 9:30, 9:40, 9:55, 10:10, 10:20 C2 : 9:10, 9:25, 9:35, 9:45, 9:55, 10:10 C3 : 9:10, 9:25, 9:40, 9:50, 10:00, 10:10 C4 : 9:10, 9:25, 9:40, 9:55, 10:05, 10:15 For Schengen visa (12.5 mins) slots are C1 : 9:12.30, 9:25. 9:37.30 C2 : 9:12.30, 9:32.30, 9:45 For others (5 mins) slots are C1 → 9:05, 9:20, 9:35 C2 → 9:05, 9:20, 9:35 For the others, the time taken to process are application is 5 mins. Time taken to process 40 applications is 40 × 5 = 200 mins.
13. Which of the following is the closest to the time when Nandini’s application process got over?
- 9:45 am
- 9:37 am
- 9:50 am
- 9:35 am
Given slots are twenty 15 minutes slots starting at 9AM and ending at 2PM. Then applicants are scheduled in each slot. Total number of applicants = 10 × 20 = 200 No. of US applications = 50% of Total = 50% of 200 = 100 Since the number of US applications was the same in all slots. So, US applications in each slot = 100/20 = 5 It is given that I, V and N were scheduled for Schengen visa processing in that order. Their slot was 9:15 AM. It means the number of Schengen applicants in each slot is at least 3. Similarly, it is given that M and O were scheduled in the 9:30AM slot in others category. So, the number of applicants in other category in each slot is at least 2. Since the number of applicants in each slots is 10. So, it can be inferred that number of Schengen and others applicants is 3 and 2 respectively. Hence the number of UK applicants is 0 in each slot. Total number of counters = 10 US counters = 4 UK counters = 2 Schengen counters = 2 Others counters = 2 Given that US and UK application requires 10 mins of processing time. Vijay was called at 9:25 A.M. (5th in line). It is possible if processing time for Schengen visa is 12.5 mins. On a particular day, I, V and N were scheduled for Schengen visa processing in given order. They had 9:15 AM slot but entered at 9:20 A.M. when they entered VPO, exactly 6 out of 10 counters were either processing applications or had finished processing ones and ready to start processing the next. Hence at 9:20 A.M. there are exactly 4 free counters. Out of these 4 free counters, 2 would be UK and 2 would be others. So, for US (Processing time is 10 mins) slots counter-wise are, C1 : 9:10, 9:20, 9:30, 9:40, 9:55, 10:10, 10:20 C2 : 9:10, 9:25, 9:35, 9:45, 9:55, 10:10 C3 : 9:10, 9:25, 9:40, 9:50, 10:00, 10:10 C4 : 9:10, 9:25, 9:40, 9:55, 10:05, 10:15 For Schengen visa (12.5 mins) slots are C1 : 9:12.30, 9:25. 9:37.30 C2 : 9:12.30, 9:32.30, 9:45 For others (5 mins) slots are C1 → 9:05, 9:20, 9:35 C2 → 9:05, 9:20, 9:35 Nandini’s application is 6th in Schengen application. So, her process will end at 9:45 AM True
14. Which of the following statements is false?
- The application process of Mahira was completed before Nandini’s.
- The application process of Mahira started after Nandini’s.
- The application process of Osman was completed before 9:45 am.
- The application process of Osman was completed before Vijay’s.
Given slots are twenty 15 minutes slots starting at 9AM and ending at 2PM. Then applicants are scheduled in each slot. Total number of applicants = 10 × 20 = 200 No. of US applications = 50% of Total = 50% of 200 = 100 Since the number of US applications was the same in all slots. So, US applications in each slot = 100/20 = 5 It is given that I, V and N were scheduled for Schengen visa processing in that order. Their slot was 9:15 AM. It means the number of Schengen applicants in each slot is at least 3. Similarly, it is given that M and O were scheduled in the 9:30AM slot in others category. So, the number of applicants in other category in each slot is at least 2. Since the number of applicants in each slots is 10. So, it can be inferred that number of Schengen and others applicants is 3 and 2 respectively. Hence the number of UK applicants is 0 in each slot. Total number of counters = 10 US counters = 4 UK counters = 2 Schengen counters = 2 Others counters = 2 Given that US and UK application requires 10 mins of processing time. Vijay was called at 9:25 A.M. (5th in line). It is possible if processing time for Schengen visa is 12.5 mins. On a particular day, I, V and N were scheduled for Schengen visa processing in given order. They had 9:15 AM slot but entered at 9:20 A.M. when they entered VPO, exactly 6 out of 10 counters were either processing applications or had finished processing ones and ready to start processing the next. Hence at 9:20 A.M. there are exactly 4 free counters. Out of these 4 free counters, 2 would be UK and 2 would be others. So, for US (Processing time is 10 mins) slots counter-wise are, C1 : 9:10, 9:20, 9:30, 9:40, 9:55, 10:10, 10:20 C2 : 9:10, 9:25, 9:35, 9:45, 9:55, 10:10 C3 : 9:10, 9:25, 9:40, 9:50, 10:00, 10:10 C4 : 9:10, 9:25, 9:40, 9:55, 10:05, 10:15 For Schengen visa (12.5 mins) slots are C1 : 9:12.30, 9:25. 9:37.30 C2 : 9:12.30, 9:32.30, 9:45 For others (5 mins) slots are C1 → 9:05, 9:20, 9:35 C2 → 9:05, 9:20, 9:35 Option 3) the process for O was completed before 9:45 A.M. True Option 2) The application process for Mahira started after Nandini’s. For Mahira, starting time is 9:30 A.M. So, for Nandini, starting time is 9:32.30. False. So, option 2 is answer.
15. When did the application processing for all US applicants get over on that day?
- 3:40 pm
- 2:05 pm
- 2:00 pm
- 2:25 pm
Given slots are twenty 15 minutes slots starting at 9AM and ending at 2PM. Then applicants are scheduled in each slot. Total number of applicants = 10 × 20 = 200 No. of US applications = 50% of Total = 50% of 200 = 100 Since the number of US applications was the same in all slots. So, US applications in each slot = 100/20 = 5 It is given that I, V and N were scheduled for Schengen visa processing in that order. Their slot was 9:15 AM. It means the number of Schengen applicants in each slot is at least 3. Similarly, it is given that M and O were scheduled in the 9:30AM slot in others category. So, the number of applicants in other category in each slot is at least 2. Since the number of applicants in each slots is 10. So, it can be inferred that number of Schengen and others applicants is 3 and 2 respectively. Hence the number of UK applicants is 0 in each slot. Total number of counters = 10 US counters = 4 UK counters = 2 Schengen counters = 2 Others counters = 2 Given that US and UK application requires 10 mins of processing time. Vijay was called at 9:25 A.M. (5th in line). It is possible if processing time for Schengen visa is 12.5 mins. On a particular day, I, V and N were scheduled for Schengen visa processing in given order. They had 9:15 AM slot but entered at 9:20 A.M. when they entered VPO, exactly 6 out of 10 counters were either processing applications or had finished processing ones and ready to start processing the next. Hence at 9:20 A.M. there are exactly 4 free counters. Out of these 4 free counters, 2 would be UK and 2 would be others. So, for US (Processing time is 10 mins) slots counter-wise are, C1 : 9:10, 9:20, 9:30, 9:40, 9:55, 10:10, 10:20 C2 : 9:10, 9:25, 9:35, 9:45, 9:55, 10:10 C3 : 9:10, 9:25, 9:40, 9:50, 10:00, 10:10 C4 : 9:10, 9:25, 9:40, 9:55, 10:05, 10:15 For Schengen visa (12.5 mins) slots are C1 : 9:12.30, 9:25. 9:37.30 C2 : 9:12.30, 9:32.30, 9:45 For others (5 mins) slots are C1 → 9:05, 9:20, 9:35 C2 → 9:05, 9:20, 9:35 From the slots, we can see that the first slot took 20 mins to complete, and after that the remaining 19 slots took 15 mins each to complete the US application process. So, Total time taken = 20 + 15 × 19 = 305 mins. Hence end time will be = 9 AM + 305 Mins = 2:05 P.M.
Correct Answer 11
0
Correct Answer 12
200
Correct Answer 13
Option 1
Correct Answer 14
Option 2
Correct Answer 15
Option 2
CAT 2023 | DILR Set 4
Direction Q.16 to 20:
The schematic diagram below shows 12 rectangular houses in a housing complex. House numbers are mentioned in the rectangles representing the houses. The houses are located in six columns – Column-A through Column-F, and two rows – Row-1 and Row-2. The houses are divided into two blocks – Block XX and Block YY. The diagram also shows two roads, one passing in front of the houses in Row-2 and another between the two blocks.
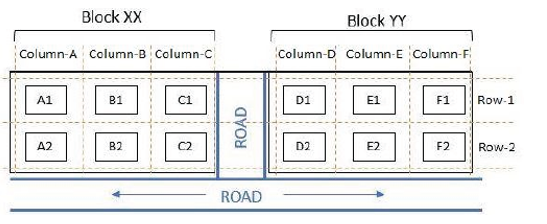
Some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The road adjacency value of a house is the number of its sides adjacent to a road. For example, the road adjacency values of C2, F2, and B1 are 2, 1, and 0, respectively. The neighbour count of a house is the number of sides of that house adjacent to occupied houses in the same block. For example, E1 and C1 can have the maximum possible neighbour counts of 3 and 2, respectively.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbour count).
The following information is also known.
- The maximum quoted price of a house in Block XX is Rs. 24 lakhs. The minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column-E.
- Row-1 has two occupied houses, one in each block.
- Both houses in Column-E are vacant. Each of Column-D and Column-F has at least one occupied house.
- There is only one house with parking space in Block YY.
16. How many houses are vacant in Block XX? (in numerial value)
 We can determine following by reading the set:
1. Row 1 has two occupied houses one in each block means one out of A1, B1, C1 is occupied. One out of D1, E1, F1 is occupied
Also, it means 4 are vacant.
2. E1 and E2 are vacant.
3. The costliest house (vacant) in block xx is worth 24 lacs.
4. The cheapest house (vacant) in block yy is worth 15 lacs.
5. One out of E1 or E2 is of worth 15 lacs.
6. There is only are house with parking space in block yy.
Let a = road adjacency value
Let b = neighbour count.
Where a = 0/1/2
Where b = 0/1/2/3
There can be 2 possibilities for the house worth 24 lacs:
Case 1: - A house has parking space:
Quoted price = 12 + 5a + 3b = 24
⇒ 5a + 3b = 12
The only possible solution is a = 0, b = 4.
But b can’t be 4 as maximum no. of neighbours can be 3.
Case 2:- House has not parking space.
Quoted price = 10 + 5a + 3b = 24
⇒ 5a + 3b = 14
⇒ a = 1, b = 3
It means the house has 1 roads adjacent and 3 neighbours i.e. occupied houses.
The only possibility is B2
So, we can determine B2 is vacant and worth 24 lacs. Also A2, B1 and C2 are unoccupied.
From condition (1), we can say A1 & C1 are unoccupied.
We can determine following by reading the set:
1. Row 1 has two occupied houses one in each block means one out of A1, B1, C1 is occupied. One out of D1, E1, F1 is occupied
Also, it means 4 are vacant.
2. E1 and E2 are vacant.
3. The costliest house (vacant) in block xx is worth 24 lacs.
4. The cheapest house (vacant) in block yy is worth 15 lacs.
5. One out of E1 or E2 is of worth 15 lacs.
6. There is only are house with parking space in block yy.
Let a = road adjacency value
Let b = neighbour count.
Where a = 0/1/2
Where b = 0/1/2/3
There can be 2 possibilities for the house worth 24 lacs:
Case 1: - A house has parking space:
Quoted price = 12 + 5a + 3b = 24
⇒ 5a + 3b = 12
The only possible solution is a = 0, b = 4.
But b can’t be 4 as maximum no. of neighbours can be 3.
Case 2:- House has not parking space.
Quoted price = 10 + 5a + 3b = 24
⇒ 5a + 3b = 14
⇒ a = 1, b = 3
It means the house has 1 roads adjacent and 3 neighbours i.e. occupied houses.
The only possibility is B2
So, we can determine B2 is vacant and worth 24 lacs. Also A2, B1 and C2 are unoccupied.
From condition (1), we can say A1 & C1 are unoccupied.
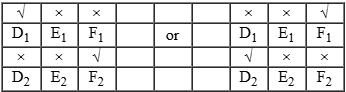
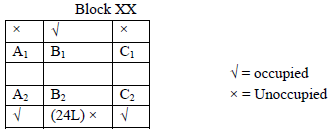 For Block YY:
Both E1 and E2 are vacant.
By condition 4, either price of E1 or E2 is 15 Lacs.
Two cases arise:-
Case 1: If E1 is of 15 Lacs.
Road adjacency value = 0.
If this house has no parking space then
10 + 5 × 0 + 3b = 15
⇒ 3b = 5 Never possible.
If E1 has parking space,
12 + 5 × 0 + 3b = 15
⇒ 3b = 3 ⇒ b = 1.
Means E1 has one occupied neighbouring house. E2 is already vacant. So, It can be either D1 or F1. So, there would be 2 possibilities
For Block YY:
Both E1 and E2 are vacant.
By condition 4, either price of E1 or E2 is 15 Lacs.
Two cases arise:-
Case 1: If E1 is of 15 Lacs.
Road adjacency value = 0.
If this house has no parking space then
10 + 5 × 0 + 3b = 15
⇒ 3b = 5 Never possible.
If E1 has parking space,
12 + 5 × 0 + 3b = 15
⇒ 3b = 3 ⇒ b = 1.
Means E1 has one occupied neighbouring house. E2 is already vacant. So, It can be either D1 or F1. So, there would be 2 possibilities
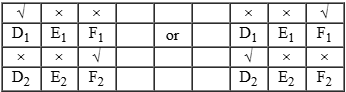
 Case 2:
If E2 is of 15 Lacs.
We already know a = 1.
If E2 has parking space:
12+ 5 × 1 + 3b = 15 ⇒ 3b = - 2 (Not possible)
If E2 has no parking space:
10 + 5 × 1 + 3b = 15 ⇒ b = 0
Means D2, E1 and F2 are vacant.
That implies D1 & F1 are occupied by condition that column D and column F has at least one occupied house. But it is a contradiction to condition 1.
So, this is an invalid case.
Answer is 3.
Case 2:
If E2 is of 15 Lacs.
We already know a = 1.
If E2 has parking space:
12+ 5 × 1 + 3b = 15 ⇒ 3b = - 2 (Not possible)
If E2 has no parking space:
10 + 5 × 1 + 3b = 15 ⇒ b = 0
Means D2, E1 and F2 are vacant.
That implies D1 & F1 are occupied by condition that column D and column F has at least one occupied house. But it is a contradiction to condition 1.
So, this is an invalid case.
Answer is 3.
17. Which of the following houses is definitely occupied?
- B1
- D2
- F2
- A1
 We can determine following by reading the set:
1. Row 1 has two occupied houses one in each block means one out of A1, B1, C1 is occupied. One out of D1, E1, F1 is occupied
Also, it means 4 are vacant.
2. E1 and E2 are vacant.
3. The costliest house (vacant) in block xx is worth 24 lacs.
4. The cheapest house (vacant) in block yy is worth 15 lacs.
5. One out of E1 or E2 is of worth 15 lacs.
6. There is only are house with parking space in block yy.
Let a = road adjacency value
Let b = neighbour count.
Where a = 0/1/2
Where b = 0/1/2/3
There can be 2 possibilities for the house worth 24 lacs:
Case 1: - A house has parking space:
Quoted price = 12 + 5a + 3b = 24
⇒ 5a + 3b = 12
The only possible solution is a = 0, b = 4.
But b can’t be 4 as maximum no. of neighbours can be 3.
Case 2:- House has not parking space.
Quoted price = 10 + 5a + 3b = 24
⇒ 5a + 3b = 14
⇒ a = 1, b = 3
It means the house has 1 roads adjacent and 3 neighbours i.e. occupied houses.
The only possibility is B2
So, we can determine B2 is vacant and worth 24 lacs. Also A2, B1 and C2 are unoccupied.
From condition (1), we can say A1 & C1 are unoccupied.
We can determine following by reading the set:
1. Row 1 has two occupied houses one in each block means one out of A1, B1, C1 is occupied. One out of D1, E1, F1 is occupied
Also, it means 4 are vacant.
2. E1 and E2 are vacant.
3. The costliest house (vacant) in block xx is worth 24 lacs.
4. The cheapest house (vacant) in block yy is worth 15 lacs.
5. One out of E1 or E2 is of worth 15 lacs.
6. There is only are house with parking space in block yy.
Let a = road adjacency value
Let b = neighbour count.
Where a = 0/1/2
Where b = 0/1/2/3
There can be 2 possibilities for the house worth 24 lacs:
Case 1: - A house has parking space:
Quoted price = 12 + 5a + 3b = 24
⇒ 5a + 3b = 12
The only possible solution is a = 0, b = 4.
But b can’t be 4 as maximum no. of neighbours can be 3.
Case 2:- House has not parking space.
Quoted price = 10 + 5a + 3b = 24
⇒ 5a + 3b = 14
⇒ a = 1, b = 3
It means the house has 1 roads adjacent and 3 neighbours i.e. occupied houses.
The only possibility is B2
So, we can determine B2 is vacant and worth 24 lacs. Also A2, B1 and C2 are unoccupied.
From condition (1), we can say A1 & C1 are unoccupied.
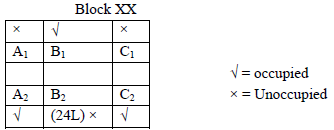 For Block YY:
Both E1 and E2 are vacant.
By condition 4, either price of E1 or E2 is 15 Lacs.
Two cases arise:-
Case 1: If E1 is of 15 Lacs.
Road adjacency value = 0.
If this house has no parking space then
10 + 5 × 0 + 3b = 15
⇒ 3b = 5 Never possible.
If E1 has parking space,
12 + 5 × 0 + 3b = 15
⇒ 3b = 3 ⇒ b = 1.
Means E1 has one occupied neighbouring house. E2 is already vacant. So, It can be either D1 or F1. So, there would be 2 possibilities
For Block YY:
Both E1 and E2 are vacant.
By condition 4, either price of E1 or E2 is 15 Lacs.
Two cases arise:-
Case 1: If E1 is of 15 Lacs.
Road adjacency value = 0.
If this house has no parking space then
10 + 5 × 0 + 3b = 15
⇒ 3b = 5 Never possible.
If E1 has parking space,
12 + 5 × 0 + 3b = 15
⇒ 3b = 3 ⇒ b = 1.
Means E1 has one occupied neighbouring house. E2 is already vacant. So, It can be either D1 or F1. So, there would be 2 possibilities
 Case 2:
If E2 is of 15 Lacs.
We already know a = 1.
If E2 has parking space:
12+ 5 × 1 + 3b = 15 ⇒ 3b = - 2 (Not possible)
If E2 has no parking space:
10 + 5 × 1 + 3b = 15 ⇒ b = 0
Means D2, E1 and F2 are vacant.
That implies D1 & F1 are occupied by condition that column D and column F has at least one occupied house. But it is a contradiction to condition 1.
So, this is an invalid case.
B1 is definitely occupied..
Case 2:
If E2 is of 15 Lacs.
We already know a = 1.
If E2 has parking space:
12+ 5 × 1 + 3b = 15 ⇒ 3b = - 2 (Not possible)
If E2 has no parking space:
10 + 5 × 1 + 3b = 15 ⇒ b = 0
Means D2, E1 and F2 are vacant.
That implies D1 & F1 are occupied by condition that column D and column F has at least one occupied house. But it is a contradiction to condition 1.
So, this is an invalid case.
B1 is definitely occupied..
18. Which of the following options best describes the number of vacant houses in Row-2?
- Either 3 or 4
- Either 2 or 3
- Exactly 3
- Exactly 2
 We can determine following by reading the set:
1. Row 1 has two occupied houses one in each block means one out of A1, B1, C1 is occupied. One out of D1, E1, F1 is occupied
Also, it means 4 are vacant.
2. E1 and E2 are vacant.
3. The costliest house (vacant) in block xx is worth 24 lacs.
4. The cheapest house (vacant) in block yy is worth 15 lacs.
5. One out of E1 or E2 is of worth 15 lacs.
6. There is only are house with parking space in block yy.
Let a = road adjacency value
Let b = neighbour count.
Where a = 0/1/2
Where b = 0/1/2/3
There can be 2 possibilities for the house worth 24 lacs:
Case 1: - A house has parking space:
Quoted price = 12 + 5a + 3b = 24
⇒ 5a + 3b = 12
The only possible solution is a = 0, b = 4.
But b can’t be 4 as maximum no. of neighbours can be 3.
Case 2:- House has not parking space.
Quoted price = 10 + 5a + 3b = 24
⇒ 5a + 3b = 14
⇒ a = 1, b = 3
It means the house has 1 roads adjacent and 3 neighbours i.e. occupied houses.
The only possibility is B2
So, we can determine B2 is vacant and worth 24 lacs. Also A2, B1 and C2 are unoccupied.
From condition (1), we can say A1 & C1 are unoccupied.
We can determine following by reading the set:
1. Row 1 has two occupied houses one in each block means one out of A1, B1, C1 is occupied. One out of D1, E1, F1 is occupied
Also, it means 4 are vacant.
2. E1 and E2 are vacant.
3. The costliest house (vacant) in block xx is worth 24 lacs.
4. The cheapest house (vacant) in block yy is worth 15 lacs.
5. One out of E1 or E2 is of worth 15 lacs.
6. There is only are house with parking space in block yy.
Let a = road adjacency value
Let b = neighbour count.
Where a = 0/1/2
Where b = 0/1/2/3
There can be 2 possibilities for the house worth 24 lacs:
Case 1: - A house has parking space:
Quoted price = 12 + 5a + 3b = 24
⇒ 5a + 3b = 12
The only possible solution is a = 0, b = 4.
But b can’t be 4 as maximum no. of neighbours can be 3.
Case 2:- House has not parking space.
Quoted price = 10 + 5a + 3b = 24
⇒ 5a + 3b = 14
⇒ a = 1, b = 3
It means the house has 1 roads adjacent and 3 neighbours i.e. occupied houses.
The only possibility is B2
So, we can determine B2 is vacant and worth 24 lacs. Also A2, B1 and C2 are unoccupied.
From condition (1), we can say A1 & C1 are unoccupied.
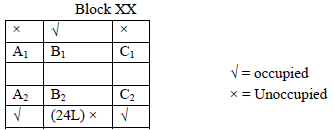 For Block YY:
Both E1 and E2 are vacant.
By condition 4, either price of E1 or E2 is 15 Lacs.
Two cases arise:-
Case 1: If E1 is of 15 Lacs.
Road adjacency value = 0.
If this house has no parking space then
10 + 5 × 0 + 3b = 15
⇒ 3b = 5 Never possible.
If E1 has parking space,
12 + 5 × 0 + 3b = 15
⇒ 3b = 3 ⇒ b = 1.
Means E1 has one occupied neighbouring house. E2 is already vacant. So, It can be either D1 or F1. So, there would be 2 possibilities
For Block YY:
Both E1 and E2 are vacant.
By condition 4, either price of E1 or E2 is 15 Lacs.
Two cases arise:-
Case 1: If E1 is of 15 Lacs.
Road adjacency value = 0.
If this house has no parking space then
10 + 5 × 0 + 3b = 15
⇒ 3b = 5 Never possible.
If E1 has parking space,
12 + 5 × 0 + 3b = 15
⇒ 3b = 3 ⇒ b = 1.
Means E1 has one occupied neighbouring house. E2 is already vacant. So, It can be either D1 or F1. So, there would be 2 possibilities
 Case 2:
If E2 is of 15 Lacs.
We already know a = 1.
If E2 has parking space:
12+ 5 × 1 + 3b = 15 ⇒ 3b = - 2 (Not possible)
If E2 has no parking space:
10 + 5 × 1 + 3b = 15 ⇒ b = 0
Means D2, E1 and F2 are vacant.
That implies D1 & F1 are occupied by condition that column D and column F has at least one occupied house. But it is a contradiction to condition 1.
So, this is an invalid case.
Exactly 3.
Case 2:
If E2 is of 15 Lacs.
We already know a = 1.
If E2 has parking space:
12+ 5 × 1 + 3b = 15 ⇒ 3b = - 2 (Not possible)
If E2 has no parking space:
10 + 5 × 1 + 3b = 15 ⇒ b = 0
Means D2, E1 and F2 are vacant.
That implies D1 & F1 are occupied by condition that column D and column F has at least one occupied house. But it is a contradiction to condition 1.
So, this is an invalid case.
Exactly 3.
19. What is the maximum possible quoted price (in lakhs of Rs.) for a vacant house in Column-E? (in numerial value)
 We can determine following by reading the set:
1. Row 1 has two occupied houses one in each block means one out of A1, B1, C1 is occupied. One out of D1, E1, F1 is occupied
Also, it means 4 are vacant.
2. E1 and E2 are vacant.
3. The costliest house (vacant) in block xx is worth 24 lacs.
4. The cheapest house (vacant) in block yy is worth 15 lacs.
5. One out of E1 or E2 is of worth 15 lacs.
6. There is only are house with parking space in block yy.
Let a = road adjacency value
Let b = neighbour count.
Where a = 0/1/2
Where b = 0/1/2/3
There can be 2 possibilities for the house worth 24 lacs:
Case 1: - A house has parking space:
Quoted price = 12 + 5a + 3b = 24
⇒ 5a + 3b = 12
The only possible solution is a = 0, b = 4.
But b can’t be 4 as maximum no. of neighbours can be 3.
Case 2:- House has not parking space.
Quoted price = 10 + 5a + 3b = 24
⇒ 5a + 3b = 14
⇒ a = 1, b = 3
It means the house has 1 roads adjacent and 3 neighbours i.e. occupied houses.
The only possibility is B2
So, we can determine B2 is vacant and worth 24 lacs. Also A2, B1 and C2 are unoccupied.
From condition (1), we can say A1 & C1 are unoccupied.
We can determine following by reading the set:
1. Row 1 has two occupied houses one in each block means one out of A1, B1, C1 is occupied. One out of D1, E1, F1 is occupied
Also, it means 4 are vacant.
2. E1 and E2 are vacant.
3. The costliest house (vacant) in block xx is worth 24 lacs.
4. The cheapest house (vacant) in block yy is worth 15 lacs.
5. One out of E1 or E2 is of worth 15 lacs.
6. There is only are house with parking space in block yy.
Let a = road adjacency value
Let b = neighbour count.
Where a = 0/1/2
Where b = 0/1/2/3
There can be 2 possibilities for the house worth 24 lacs:
Case 1: - A house has parking space:
Quoted price = 12 + 5a + 3b = 24
⇒ 5a + 3b = 12
The only possible solution is a = 0, b = 4.
But b can’t be 4 as maximum no. of neighbours can be 3.
Case 2:- House has not parking space.
Quoted price = 10 + 5a + 3b = 24
⇒ 5a + 3b = 14
⇒ a = 1, b = 3
It means the house has 1 roads adjacent and 3 neighbours i.e. occupied houses.
The only possibility is B2
So, we can determine B2 is vacant and worth 24 lacs. Also A2, B1 and C2 are unoccupied.
From condition (1), we can say A1 & C1 are unoccupied.
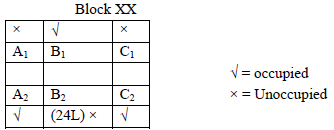 For Block YY:
Both E1 and E2 are vacant.
By condition 4, either price of E1 or E2 is 15 Lacs.
Two cases arise:-
Case 1: If E1 is of 15 Lacs.
Road adjacency value = 0.
If this house has no parking space then
10 + 5 × 0 + 3b = 15
⇒ 3b = 5 Never possible.
If E1 has parking space,
12 + 5 × 0 + 3b = 15
⇒ 3b = 3 ⇒ b = 1.
Means E1 has one occupied neighbouring house. E2 is already vacant. So, It can be either D1 or F1. So, there would be 2 possibilities
For Block YY:
Both E1 and E2 are vacant.
By condition 4, either price of E1 or E2 is 15 Lacs.
Two cases arise:-
Case 1: If E1 is of 15 Lacs.
Road adjacency value = 0.
If this house has no parking space then
10 + 5 × 0 + 3b = 15
⇒ 3b = 5 Never possible.
If E1 has parking space,
12 + 5 × 0 + 3b = 15
⇒ 3b = 3 ⇒ b = 1.
Means E1 has one occupied neighbouring house. E2 is already vacant. So, It can be either D1 or F1. So, there would be 2 possibilities
 Case 2:
If E2 is of 15 Lacs.
We already know a = 1.
If E2 has parking space:
12+ 5 × 1 + 3b = 15 ⇒ 3b = - 2 (Not possible)
If E2 has no parking space:
10 + 5 × 1 + 3b = 15 ⇒ b = 0
Means D2, E1 and F2 are vacant.
That implies D1 & F1 are occupied by condition that column D and column F has at least one occupied house. But it is a contradiction to condition 1.
So, this is an invalid case.
Maximum possible quoted price = 10 + 5 × 1 + 3 ×2 = 21 Lacs.
Case 2:
If E2 is of 15 Lacs.
We already know a = 1.
If E2 has parking space:
12+ 5 × 1 + 3b = 15 ⇒ 3b = - 2 (Not possible)
If E2 has no parking space:
10 + 5 × 1 + 3b = 15 ⇒ b = 0
Means D2, E1 and F2 are vacant.
That implies D1 & F1 are occupied by condition that column D and column F has at least one occupied house. But it is a contradiction to condition 1.
So, this is an invalid case.
Maximum possible quoted price = 10 + 5 × 1 + 3 ×2 = 21 Lacs.
20. Which house in Block YY has parking space?
- F1
- E2
- E1
- F2
 We can determine following by reading the set:
1. Row 1 has two occupied houses one in each block means one out of A1, B1, C1 is occupied. One out of D1, E1, F1 is occupied
Also, it means 4 are vacant.
2. E1 and E2 are vacant.
3. The costliest house (vacant) in block xx is worth 24 lacs.
4. The cheapest house (vacant) in block yy is worth 15 lacs.
5. One out of E1 or E2 is of worth 15 lacs.
6. There is only are house with parking space in block yy.
Let a = road adjacency value
Let b = neighbour count.
Where a = 0/1/2
Where b = 0/1/2/3
There can be 2 possibilities for the house worth 24 lacs:
Case 1: - A house has parking space:
Quoted price = 12 + 5a + 3b = 24
⇒ 5a + 3b = 12
The only possible solution is a = 0, b = 4.
But b can’t be 4 as maximum no. of neighbours can be 3.
Case 2:- House has not parking space.
Quoted price = 10 + 5a + 3b = 24
⇒ 5a + 3b = 14
⇒ a = 1, b = 3
It means the house has 1 roads adjacent and 3 neighbours i.e. occupied houses.
The only possibility is B2
So, we can determine B2 is vacant and worth 24 lacs. Also A2, B1 and C2 are unoccupied.
From condition (1), we can say A1 & C1 are unoccupied.
We can determine following by reading the set:
1. Row 1 has two occupied houses one in each block means one out of A1, B1, C1 is occupied. One out of D1, E1, F1 is occupied
Also, it means 4 are vacant.
2. E1 and E2 are vacant.
3. The costliest house (vacant) in block xx is worth 24 lacs.
4. The cheapest house (vacant) in block yy is worth 15 lacs.
5. One out of E1 or E2 is of worth 15 lacs.
6. There is only are house with parking space in block yy.
Let a = road adjacency value
Let b = neighbour count.
Where a = 0/1/2
Where b = 0/1/2/3
There can be 2 possibilities for the house worth 24 lacs:
Case 1: - A house has parking space:
Quoted price = 12 + 5a + 3b = 24
⇒ 5a + 3b = 12
The only possible solution is a = 0, b = 4.
But b can’t be 4 as maximum no. of neighbours can be 3.
Case 2:- House has not parking space.
Quoted price = 10 + 5a + 3b = 24
⇒ 5a + 3b = 14
⇒ a = 1, b = 3
It means the house has 1 roads adjacent and 3 neighbours i.e. occupied houses.
The only possibility is B2
So, we can determine B2 is vacant and worth 24 lacs. Also A2, B1 and C2 are unoccupied.
From condition (1), we can say A1 & C1 are unoccupied.
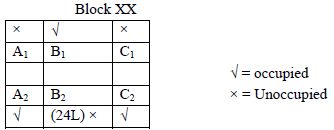 For Block YY:
Both E1 and E2 are vacant.
By condition 4, either price of E1 or E2 is 15 Lacs.
Two cases arise:-
Case 1: If E1 is of 15 Lacs.
Road adjacency value = 0.
If this house has no parking space then
10 + 5 × 0 + 3b = 15
⇒ 3b = 5 Never possible.
If E1 has parking space,
12 + 5 × 0 + 3b = 15
⇒ 3b = 3 ⇒ b = 1.
Means E1 has one occupied neighbouring house. E2 is already vacant. So, It can be either D1 or F1. So, there would be 2 possibilities
For Block YY:
Both E1 and E2 are vacant.
By condition 4, either price of E1 or E2 is 15 Lacs.
Two cases arise:-
Case 1: If E1 is of 15 Lacs.
Road adjacency value = 0.
If this house has no parking space then
10 + 5 × 0 + 3b = 15
⇒ 3b = 5 Never possible.
If E1 has parking space,
12 + 5 × 0 + 3b = 15
⇒ 3b = 3 ⇒ b = 1.
Means E1 has one occupied neighbouring house. E2 is already vacant. So, It can be either D1 or F1. So, there would be 2 possibilities
 Case 2:
If E2 is of 15 Lacs.
We already know a = 1.
If E2 has parking space:
12+ 5 × 1 + 3b = 15 ⇒ 3b = - 2 (Not possible)
If E2 has no parking space:
10 + 5 × 1 + 3b = 15 ⇒ b = 0
Means D2, E1 and F2 are vacant.
That implies D1 & F1 are occupied by condition that column D and column F has at least one occupied house. But it is a contradiction to condition 1.
So, this is an invalid case.
E1 has parking space.
Case 2:
If E2 is of 15 Lacs.
We already know a = 1.
If E2 has parking space:
12+ 5 × 1 + 3b = 15 ⇒ 3b = - 2 (Not possible)
If E2 has no parking space:
10 + 5 × 1 + 3b = 15 ⇒ b = 0
Means D2, E1 and F2 are vacant.
That implies D1 & F1 are occupied by condition that column D and column F has at least one occupied house. But it is a contradiction to condition 1.
So, this is an invalid case.
E1 has parking space.
Correct Answer 16
3
Correct Answer 17
Option 1
Correct Answer 18
Option 3
Correct Answer 19
21
Correct Answer 20
Option 3