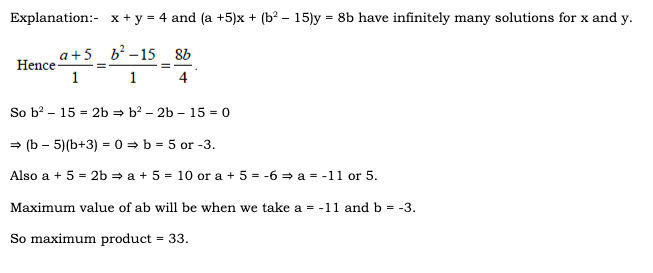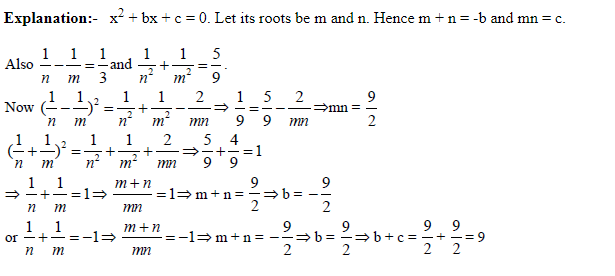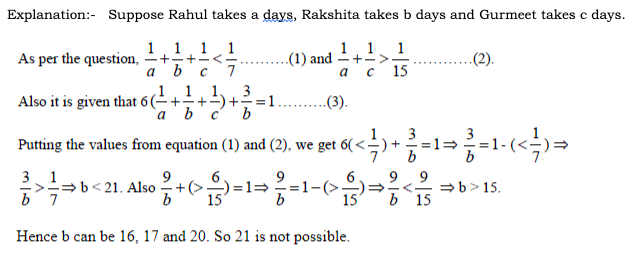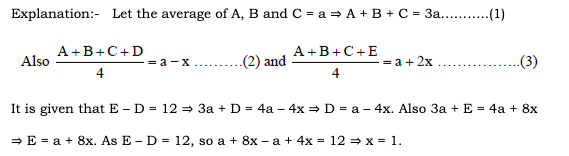Anil mixes cocoa with sugar in the ratio 3 : 2 to prepare mixture A, and coffee with sugar in the ratio 7 : 3 to prepare mixture B. He combines mixtures A and B in the ratio 2 : 3 to make a new mixture C. If he mixes C with an equal amount of milk to make a drink, then the percentage of sugar in this drink will be
Rahul, Rakshita and Gurmeet, working together, would have taken more than 7 days to finish a job. On the other hand, Rahul and Gurmeet, working together would have taken less than 15 days to finish the job. However, they all worked together for 6 days, followed by Rakshita, who worked alone for 3 more days to finish the job. If Rakshita had worked alone on the job then the number of days she would have taken to finish the job, cannot be
The population of a town in 2020 was 100000. The population decreased by y% from the year 2020 to 2021, and increased by x% from the year 2021 to 2022, where x and y are two natural numbers. If population in 2022 was greater than the population in 2020 and the difference between x and y is 10, then the lowest possible population of the town in 2021 was
Population in 2020 = 100000 It is given that there is y% decrease in population from 2020 to 2021 and x% increase in population from 2021 to 2022. Also it is given that population of 2022 is greater than population of 2020. This means x is greater than y because had it been x = y, even then population of 2022 would have been less the population of 2020. Difference between x and y is 10. Minimum popuation in 2021 is to be calculated by options:: Option (1) which is 72000 ⇒ y = 28 and x = 38 ⇒ Population in 2022 = 72000 × 1.38 = 99360. Hence it is possible. Option (2) which is 75000 ⇒ y = 25 and x = 35 ⇒ Population in 2022 = 75000 × 1.35 = 101250. Hence it is possible. Option (3) which is 74000 ⇒ y = 26 and x = 36 ⇒ Population in 2022 = 74000 × 1.36 = 100640. Hence it is possible. Option (4) which is 73000 ⇒ y = 27 and x = 37 ⇒ Population in 2022 = 73000 × 1.37 = 100010. Since 100010 is minimum of all ⇒ 73000 is the answer.
A merchant purchases a cloth at a rate of Rs.100 per meter and receives 5 cm length of cloth free for every 100 cm length of cloth purchased by him. He sells the same cloth at a rate of Rs.110 per meter but cheats his customers by giving 95 cm length of cloth for every 100 cm length of cloth purchased by the customers. If the merchant provides a 5% discount, the resulting profit earned by him is
There are three persons A, B and C in a room. If a person D joins the room, the average weight of the persons in the room reduces by x kg. Instead of D, if person E joins the room, the average weight of the persons in the room increases by 2x kg. If the weight of E is 12 kg more than that of D, then the value of x is
A boat takes 2 hours to travel downstream a river from port A to port B, and 3 hours to return to port A. Another boat takes a total of 6 hours to travel from port B to port A and return to port B. If the speeds of the boats and the river are constant, then the time, in hours, taken by the slower boat to travel from port A to port B is
Gautam and Suhani, working together, can finish a job in 20 days. If Gautam does only 60% of his usual work on a day, Suhani must do 150% of her usual work on that day to exactly make up for it. Then, the number of days required by the faster worker to complete the job working alone is (in numerical value)
Let us assume the efficiency of Gautam as G and efficiency of Suhani as S. Hence we get the equation as (G + S)20 = (0.6G + 1.5S)20 ⇒ 4G = 5S ⇒ G : S = 5 : 4. So ratio of time taken by G and S will be in the ratio 4 : 5. Lets assume Gautam takes 4x days and Suhani takes 5x days to complete the work 1/4x+1/5x = 1/20 = x = 9 Hence faster worker takes 36 days to complete the work.
The number of coins collected per week by two coin-collectors A and B are In the ratio 3 : 4. If the total number of coins collected by A in 5 weeks is a multiple of 7, and the total number of coins collected by B in 3 weeks is a multiple of 24, then the minimum possible number of coins collected by A in one week is (in numerical value)
A : B = 3 : 4. Let us take collection/week of A as 3x and B as 4x ⇒ In 5 weeks, A collected 3x × 5 = 15x which is a multiple of 7. In 3 weeks, B collected 4x × 3 = 12x which is a multiple of 24 ⇒ x is an even multiple of 7 ⇒ Lowest possible value of x is 14. So number of coins collected by A in one week is 3x = 3 × 14 = 42.
A fruit seller has a stock of mangoes, bananas and apples with at least one fruit of each type. At the beginning of a day, the number of mangoes make up 40% of his stock. That day, he sells half of the mangoes, 96 bananas and 40% of the apples. At the end of the day, he ends up selling 50% of the fruits. The smallest possible total number of fruits in the stock at the beginning of the day is (in numerical value)
Let ∆ABC be an isosceles triangle such that AB and AC are of equal length. AD is the altitude from A on BC and BE is the altitude from B on AC. If AD and BE intersect at O such that ∠AOB = 105°, then AD/BE equals
Let an = 46 + 8n and bn = 98 + 4n be two sequences for natural numbers n ≤ 100. Then, the sum of all terms common to both the sequences is
an = 46 + 8n, bn = 98 + 4n. Putting the values of n as 1, 2, 3….. in the 1st sequence we get values as 54, 62, 70…… Putting the values of n as 1, 2, 3….. in the 2nd sequence we get values as 102, 106, 110, 114…… So the common terms to both the sequences is 102, 110, 118…………. But last term in the 1st sequence is 846 when we put n = 100 and last term in the 2nd sequence is 498 when we put n = 100. Also the common sequence is 102, 110…….. is of the form 8k + 6. Hence last number of this form in this sequence is 494. So we get the final sequence as 102, 110, 118, …….494. Number of terms in this sequence: 102 + (n -1) 8 = 494 ⇒ n = 50. Sum of these terms = 50/2 (102 + 494) = 14900.
Suppose f(x, y) ;is a real valued function such that f(3x + 2y, 2x- 5y) = 19x, for all real numbers x and y. The value of x for which f(x, 2x) = 27, is (in numerical value)
Given that f(3x+2y, 2x – 5y) = 19x. Multiplying 1st function by 5 and 2nd function by 2, we get 15x + 10y and 4x – 10y. Now on adding these 2 functions, we get 15x + 10y + 4x – 10y = 19x. Using the same operation for f(x,2x), we get 5x + 2(2x) = 27 ⇒ 9x = 27 ⇒ x = 3
We at Quantifiers understand and deliver on the personal attention each of our students requires. Whether it is through our pedagogy that enables non-engineers or non-math background students, our constant effort to proactively provide solutions, or our focus on our student’s goals.
