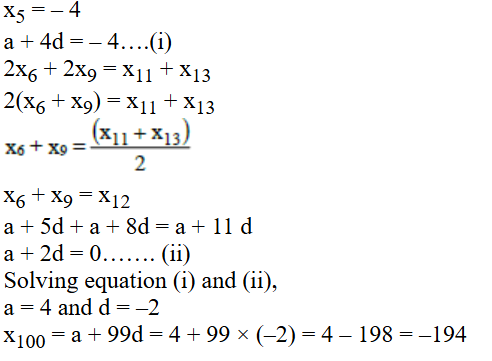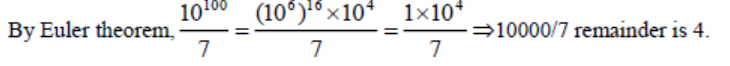Here to form all 4-digit numbers using the distinct non-zero digits a, b, c, d and each digit appears exactly once in each position across all permutations.
The total number of 4 – digit numbers is 4! = 24
Each digit appears 24/4 = 6 times in each place (thousands, hundreds, tens, and units)
For a given digit x, its total contributions are,
x × (1000 + 100 + 10 + 1) × 6 = x × 1111 × 6 = 6666x.
The sum of all numbers is:
6 × 1111 × (a + b + c + d) = 6666 (a + b + c + d).
6666 (a + b + c + d) = 153310 + n,
where n is a single-digit natural number.
Divide 153310 by 6666 ⇒ a + b + c + d = 153310/6666 = 23 (approx)
⇒ 6666 × 23 = 153318 ⇒ 153310 + n = 153318
⇒ n = 153318 – 153310 = 8
The value of a + b + c + d + n = 23 + 8 = 31
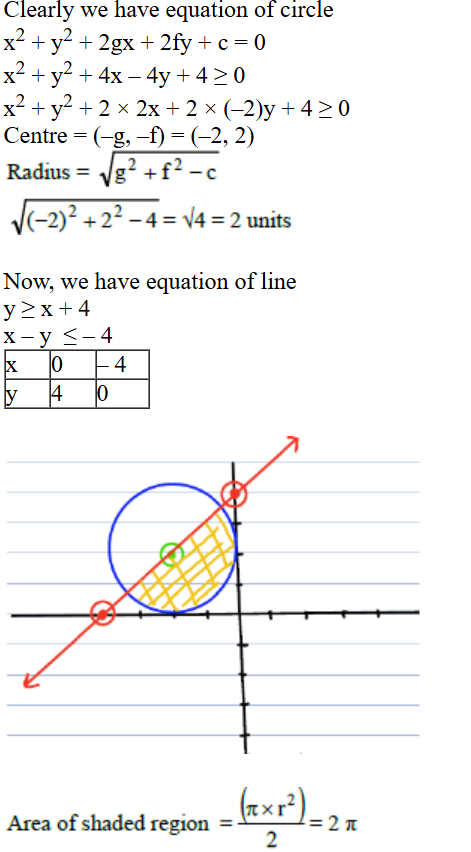














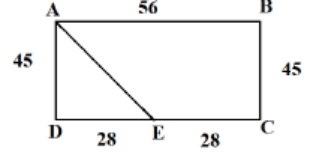 ABCD is a rectangle, E is a mid-point of D and C.
ΔADE is a right angle triangle by applying Pythagorean theorem, AE = 53.
Using the formula to calculate area of triangle = radius of incircle × Semi perimeter.
1/2 × 28 × 45 = r × (45+28+53/2)
r = 10
ABCD is a rectangle, E is a mid-point of D and C.
ΔADE is a right angle triangle by applying Pythagorean theorem, AE = 53.
Using the formula to calculate area of triangle = radius of incircle × Semi perimeter.
1/2 × 28 × 45 = r × (45+28+53/2)
r = 10