CAT 2024 DILR - Slot 1 Past Year Questions
CAT 2024 | DILR Set 1
Direction Q.1 to 4:
The chart below shows the price data for seven shares – A, B, C, D, E, F, and G as a candlestick plot for a particular day. The vertical axis shows the price of the share in rupees. A share whose closing price (price at the end of the day) is more than its opening price (price at the start of the day) is called a bullish share; otherwise, it is called a bearish share. All bullish and bearish shares are shown in green and red colour respectively.
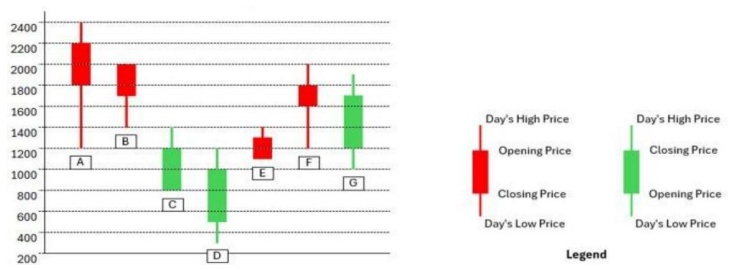
1. Daily Share Price Variability (SPV) is defined as (Day's high price - Day's low price) / (Average of the opening and closing prices during the day). Which among the shares A, C, D and F had the highest SPV on that day?
- F
- A
- C
- D
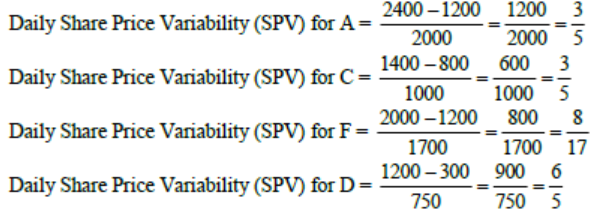 We can see that value of Daily Share Price Variability (SPV) for D is max as it is the only value which is greater than 1. All other values are less than 1. Hence option D.
We can see that value of Daily Share Price Variability (SPV) for D is max as it is the only value which is greater than 1. All other values are less than 1. Hence option D.
2. Daily Share Price Variability (SPV) is defined as (Day's high price - Day's low price) / (Average of the opening and closing prices during the day). How many shares had an SPV greater than 0.5 on that day?
 From the above table, we can see that value of SPV of 4 shares i.e A, C, D and G is greater than 0.5. Hence 4 is the answer.
From the above table, we can see that value of SPV of 4 shares i.e A, C, D and G is greater than 0.5. Hence 4 is the answer.
3. Daily loss for a share is defined as (Opening price - Closing price) / (Opening price). Which among the shares A, B, F and G had the highest daily loss on that day?
- F
- B
- A
- G
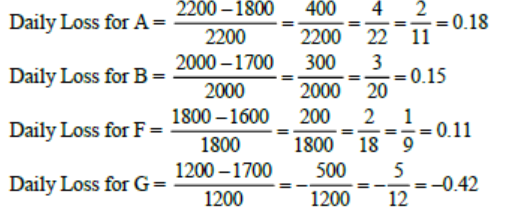 From the above table, we can see that value of Daily Loss for A is maximum. Hence option C.
From the above table, we can see that value of Daily Loss for A is maximum. Hence option C.
4. What would have been the percentage wealth gain for a trader, who bought equal numbers of all bullish shares at opening price and sold them at their day's high?
- 72%
- 80%
- 50%
- 100%
As seen from the graph, the bullish shares are C, D and G.
Let us assume he purchases one share each of C, D and G.
CP of one share of C = 800 and SP of one share of C = 1400
CP of one share of D = 500 and SP of one share of D = 1200
CP of one share of G = 1200 and SP of one share of G = 1900
So Total Cost of purchasing one share of each of C, D and G = 800 + 500 + 1200 = 2500
Total Selling Price of one share of each of C, D and G = 1400 + 1200 + 1900 = 4500.
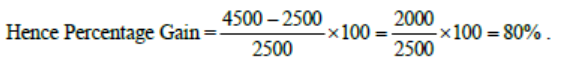
Correct Answer 1
Option D
Correct Answer 2
4
Correct Answer 3
Option C
Correct Answer 4
Option B
CAT 2024 | DILR Set 2
Direction Q.5 to 9:
Two students, Amiya and Ramya are the only candidates in an election for the position of class representative. Students will vote based on the intensity level of Amiya’s and Ramya’s campaigns and the type of campaigns they run. Each campaign is said to have a level of 1 if it is a staid campaign and a level of 2 if it is a vigorous campaign. Campaigns can be of two types, they can either focus on issues, or on attacking the other candidate.
If Amiya and Ramya both run campaigns focusing on issues, then
The percentage of students voting in the election will be 20 times the sum of the levels of campaigning of the two students. For example, if Amiya and Ramya both run vigorous campaigns, then 20 × (2 + 2)%, that is, 80% of the students will vote in the election. – Among voting students, the percentage of votes for each candidate will be proportional to the levels of their campaigns. For example, if Amiya runs a staid (i.e., level 1) campaign while Ramya runs a vigorous (i.e., level 2) campaign, then Amiya will receive 1/3 of the votes cast, and Ramya will receive the other 2/3.
The above-mentioned percentages change as follows if at least one of them runs a campaign attacking their opponent.
- If Amiya runs a campaign attacking Ramya and Ramya runs a campaign focusing on issues, then 10% of the students who would have otherwise voted for Amiya will vote for Ramya, and another 10% who would have otherwise voted for Amiya, will not vote at all.
- If Ramya runs a campaign attacking Amiya and Amiya runs a campaign focusing on issues, then 20% of the students who would have otherwise voted for Ramya will vote for Amiya, and another 5% who would have otherwise voted for Ramya, will not vote at all.
- If both run campaigns attacking each other, then 10% of the students who would have otherwise voted for them had they run campaigns focusing on issues, will not vote at all.
5. If both of them run staid campaigns attacking the other, then what percentage of students will vote in the election?
- 60%
- 64%
- 40%
- 36%
Explanation: If both of them run staid campaigns focussing on issues, then the percentage of students voting in the election will be 20 times the sum of the levels of campaigning of the two students. So the percentage would be 20(1 + 1) % = 40%. But as both of them run staid campaigns attacking the other, then 10% of 40% will not vote at all. Hence answer would be 90% of 40% which is equal to 36%.
6. What is the minimum percentage of students who will vote in the election?
- 36%
- 38%
- 32%
- 40%
Minimum percentage of students who will vote will be obtained when they run staid campaign as it of level 1. Also if they run staid campaigns attacking the other, then percentage voting would be further reduced. So minimum percentage will be obtained as 90% of 20(1 + 1)% = 90% of 40% = 36%.
7. If Amiya runs a campaign focusing on issues, then what is the maximum percentage of votes that she can get?
- 44%
- 40%
- 48%
- 36%
If both of them run vigorous campaigns focussing on issues, then the percentage of students voting in the election will be 20 times the sum of the levels of campaigning of the two students. So the percentage would be 20(2+2) % = 80%. Hence each of them would get 40% votes. It is given that Amiya runs a campaign focusing on issues. To maximise percentage of votes she gets, will be obtained when Ramya run a campaign attacking their opponent. So the reduction in the percentage of votes obtained by Ramya would be 20% of 40% = 8% which would be added to percentage of votes of Amiya. So Amiya would get 40% + 8% = 48% votes. Also 5% who would have otherwise voted for Ramya, will not vote at all. Hence total reduction in the percentage of votes for Ramya would be 8% + 5% of 40% = 10%. So answer of this question is 48%.
8. If Ramya runs a campaign attacking Amiya, then what is the minimum percentage of votes that she is guaranteed to get?
- 15%
- 30%
- 12%
- 18%
Minimum percentage of students who will vote will be obtained when they run staid campaign as it of level 1. If both of them run staid campaigns focussing on issues, then the percentage of students voting in the election will be 20 times the sum of the levels of campaigning of the two students. So the percentage would be 20(1 + 1) % = 40%. Hence each of them would get 20% votes. It is given that Ramya runs a campaign attacking their opponent. So the reduction in the percentage of votes obtained by Ramya would be 20% of 20% = 4% which would be added to percentage of votes of Amiya. Also 5% who would have otherwise voted for Ramya, will not vote at all. Hence total reduction in the percentage of votes for Ramya would be 4% + 5% of 20% = 4% + 1% = 5%. So minimum percentage of votes that she is guaranteed to get will be 20% – 5% = 15%.
9. What is the maximum possible voting margin with which one of the candidates can win?
- 29%
- 26%
- 20%
- 28%
Maximum possible voting margin with which one of the candidates can win will be obtained when one of them runs vigorous campaign and the other runs staid campaign. If Amiya runs vigorous campaign focussing on issues and Ramya runs staid campaigns focussing on issues, then the percentage of students voting in the election will be 20 times the sum of the levels of campaigning of the two students. So the percentage would be 20(2+1) % = 60%. Hence Amiya would get 40% votes and Ramya would get 40% votes. Now if Ramya runs a campaign attacking their opponent. So the reduction in the percentage of votes obtained by Ramya would be 20% of 20% = 4% which would be added to percentage of votes of Amiya. So Amiya would get 40% + 4% = 44% votes. Also 5% who would have otherwise voted for Ramya, will not vote at all. Hence total reduction in the percentage of votes for Ramya would be 4% + 5% of 20% = 4% + 1% = 5%. So minimum percentage of votes that she is guaranteed to get will be 20% – 5% = 15%. Hence maximum voting margin will be 44% – 15% = 29%.
Correct Answer 5
Option D
Correct Answer 6
Option D
Correct Answer 7
Option C
Correct Answer 8
Option A
Correct Answer 9
Option A
CAT 2024 | DILR Set 3
Direction Q.10 to 14:
A new game show on TV has 100 boxes numbered 1, 2, …, 100 in a row, each containing a mystery prize. The prizes are items of different types, a, b, c,… , in decreasing order of value. The most expensive item is of type a, a diamond ring, and there is exactly one of these. You are told that the number of items at least doubles as you move to the next type. For example, there would be at least twice as many items of type b as of type a, at least twice as many items of type c as of type b and so on. There is no particular order in which the prizes are placed in the boxes.
The following additional facts are known about the schedule of games in the tournament.
- Each team played against a team from the other group in Round 8.
- In Round 4 and Round 7, the match-ups, that is the pair of teams playing against each other, were identical. In Round 5 and Round 8 , the match-ups were identical.
- Team 4 played Team 6 in both Round 1 and Round 2.
- Team 1 played Team 5 ONLY once and that was in Round 2.
- Team 3 played Team 4 in Round 3. Team 1 played Team 6 in Round 6.
- In Round 8, Team 3 played Team 6, while Team 2 played Team 5.
10. How many rounds were there in the tournament?
Explanation: It is given that the 6 teams are divided into two groups containing 3 teams each. As each team in the same group plays every other team once and in the other group twice, so there would be 3 matches among teams of same group and 6 matches among teams of different group. Hence we can find the total matches in the tournament as 3 + 3 + 6 + 6 + 6 = 24.
Also every team plays exactly one game in one round means each round will have 3 matches involving each team. Hence there will be 8 rounds in the tournament.
Now we will further analyse the given information:
As we can see that Team 3 played against Team 6 twice, Team 2 played against Team 5 twice and Team 1 played against Team 4 twice, so Teams 3 & 6, 2 & 5 and 1 & 4 are of different groups.
Now considering points 3 and 4, we get the information that Teams 4 and 6 are of different groups and Teams 1 and 5 are of same group.
Hence we can say that Teams 1, 5 and 6 make a group (say Group I) and correspondingly Teams 2, 3 and 4 (say Group II) make the other group.
So we can list down the matches which will be played among teams of Group I and Group II
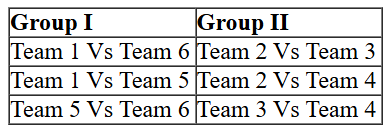 Also we can make a list of matches which were played between teams of different groups:
Also we can make a list of matches which were played between teams of different groups: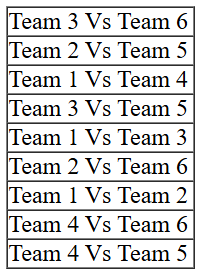 From point 6, it is given that Team 3 played Team 8 and Team 2 played Team 5. Clubbing this information with the information in point 1 that each team played against a team from the other group in Round 8, we can surely conclude that the 3rd match of Round 8 must have been played between Team 1 and 4.
Also as per point 2, match ups of Round 5 and Round 8 were identical. Hence we get the details of matches played in Round 5.
Now using information given in points 3, 4, 5 and 6, we will find the details of matches played in various rounds and put the information in a table where alphabet T stands for Team:
From point 6, it is given that Team 3 played Team 8 and Team 2 played Team 5. Clubbing this information with the information in point 1 that each team played against a team from the other group in Round 8, we can surely conclude that the 3rd match of Round 8 must have been played between Team 1 and 4.
Also as per point 2, match ups of Round 5 and Round 8 were identical. Hence we get the details of matches played in Round 5.
Now using information given in points 3, 4, 5 and 6, we will find the details of matches played in various rounds and put the information in a table where alphabet T stands for Team:
 As it is given that every team plays exactly one game in each round, so we can see that T6 would be definitely there in Round 4 and Round 7. Considering the list of matches given for different groups, only T2 is left to play against T6. Hence T2 and T6 would play against each other in Round 4 and 7.
Also match between T2 and T4 is to be played only once. This will be necessarily played in Round 6 as T4 is already playing in Rounds 1, 2 and 3.
Also match between T1 and T2 is to be played twice. This will be necessarily played in Round 1 and Round 3. It means match between T5 and T6 which is to be played only once will be in Round 3.
Also match between T4 and T5 is to be played twice. This will be necessarily played in Round 4 and Round 7. It means match between T1 and T3 which is to be played twice would also be played in Round 4 and Round 7.
So after filling all the above information, we get the final table as follows :
As it is given that every team plays exactly one game in each round, so we can see that T6 would be definitely there in Round 4 and Round 7. Considering the list of matches given for different groups, only T2 is left to play against T6. Hence T2 and T6 would play against each other in Round 4 and 7.
Also match between T2 and T4 is to be played only once. This will be necessarily played in Round 6 as T4 is already playing in Rounds 1, 2 and 3.
Also match between T1 and T2 is to be played twice. This will be necessarily played in Round 1 and Round 3. It means match between T5 and T6 which is to be played only once will be in Round 3.
Also match between T4 and T5 is to be played twice. This will be necessarily played in Round 4 and Round 7. It means match between T1 and T3 which is to be played twice would also be played in Round 4 and Round 7.
So after filling all the above information, we get the final table as follows :
 Now all the questions can be answered.
As shown, there were 8 Rounds in the tournament.
Now all the questions can be answered.
As shown, there were 8 Rounds in the tournament.
11. What is the number of the team that played Team 1 in Round 5?
It is given that the 6 teams are divided into two groups containing 3 teams each. As each team in the same group plays every other team once and in the other group twice, so there would be 3 matches among teams of same group and 6 matches among teams of different group. Hence we can find the total matches in the tournament as 3 + 3 + 6 + 6 + 6 = 24.
Also every team plays exactly one game in one round means each round will have 3 matches involving each team. Hence there will be 8 rounds in the tournament.
Now we will further analyse the given information:
As we can see that Team 3 played against Team 6 twice, Team 2 played against Team 5 twice and Team 1 played against Team 4 twice, so Teams 3 & 6, 2 & 5 and 1 & 4 are of different groups.
Now considering points 3 and 4, we get the information that Teams 4 and 6 are of different groups and Teams 1 and 5 are of same group.
Hence we can say that Teams 1, 5 and 6 make a group (say Group I) and correspondingly Teams 2, 3 and 4 (say Group II) make the other group.
So we can list down the matches which will be played among teams of Group I and Group II
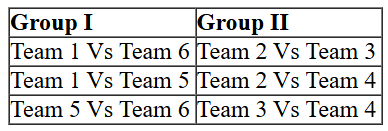 Also we can make a list of matches which were played between teams of different groups::
Also we can make a list of matches which were played between teams of different groups::
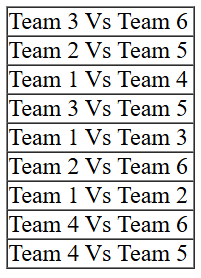 From point 6, it is given that Team 3 played Team 8 and Team 2 played Team 5. Clubbing this information with the information in point 1 that each team played against a team from the other group in Round 8, we can surely conclude that the 3rd match of Round 8 must have been played between Team 1 and 4.
Also as per point 2, match ups of Round 5 and Round 8 were identical. Hence we get the details of matches played in Round 5.
Now using information given in points 3, 4, 5 and 6, we will find the details of matches played in various rounds and put the information in a table where alphabet T stands for Team:
From point 6, it is given that Team 3 played Team 8 and Team 2 played Team 5. Clubbing this information with the information in point 1 that each team played against a team from the other group in Round 8, we can surely conclude that the 3rd match of Round 8 must have been played between Team 1 and 4.
Also as per point 2, match ups of Round 5 and Round 8 were identical. Hence we get the details of matches played in Round 5.
Now using information given in points 3, 4, 5 and 6, we will find the details of matches played in various rounds and put the information in a table where alphabet T stands for Team:
 As it is given that every team plays exactly one game in each round, so we can see that T6 would be definitely there in Round 4 and Round 7. Considering the list of matches given for different groups, only T2 is left to play against T6. Hence T2 and T6 would play against each other in Round 4 and 7.
Also match between T2 and T4 is to be played only once. This will be necessarily played in Round 6 as T4 is already playing in Rounds 1, 2 and 3.
Also match between T1 and T2 is to be played twice. This will be necessarily played in Round 1 and Round 3. It means match between T5 and T6 which is to be played only once will be in Round 3.
Also match between T4 and T5 is to be played twice. This will be necessarily played in Round 4 and Round 7. It means match between T1 and T3 which is to be played twice would also be played in Round 4 and Round 7.
So after filling all the above information, we get the final table as follows :
As it is given that every team plays exactly one game in each round, so we can see that T6 would be definitely there in Round 4 and Round 7. Considering the list of matches given for different groups, only T2 is left to play against T6. Hence T2 and T6 would play against each other in Round 4 and 7.
Also match between T2 and T4 is to be played only once. This will be necessarily played in Round 6 as T4 is already playing in Rounds 1, 2 and 3.
Also match between T1 and T2 is to be played twice. This will be necessarily played in Round 1 and Round 3. It means match between T5 and T6 which is to be played only once will be in Round 3.
Also match between T4 and T5 is to be played twice. This will be necessarily played in Round 4 and Round 7. It means match between T1 and T3 which is to be played twice would also be played in Round 4 and Round 7.
So after filling all the above information, we get the final table as follows :
 Now all the questions can be answered.
As shown, Team 4 played Team 1 in Round 5.
Now all the questions can be answered.
As shown, Team 4 played Team 1 in Round 5.
12. Which team among the teams numbered 2, 3, 4, and 5 was not part of the same group?
- 3
- 2
- 4
- 5
Explanation: It is given that the 6 teams are divided into two groups containing 3 teams each. As each team in the same group plays every other team once and in the other group twice, so there would be 3 matches among teams of same group and 6 matches among teams of different group. Hence we can find the total matches in the tournament as 3 + 3 + 6 + 6 + 6 = 24.
Also every team plays exactly one game in one round means each round will have 3 matches involving each team. Hence there will be 8 rounds in the tournament.
Now we will further analyse the given information:
As we can see that Team 3 played against Team 6 twice, Team 2 played against Team 5 twice and Team 1 played against Team 4 twice, so Teams 3 & 6, 2 & 5 and 1 & 4 are of different groups.
Now considering points 3 and 4, we get the information that Teams 4 and 6 are of different groups and Teams 1 and 5 are of same group.
Hence we can say that Teams 1, 5 and 6 make a group (say Group I) and correspondingly Teams 2, 3 and 4 (say Group II) make the other group.
So we can list down the matches which will be played among teams of Group I and Group II
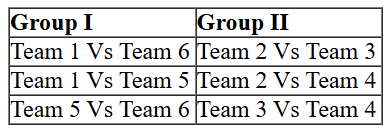 Also we can make a list of matches which were played between teams of different groups::
Also we can make a list of matches which were played between teams of different groups::
 From point 6, it is given that Team 3 played Team 8 and Team 2 played Team 5. Clubbing this information with the information in point 1 that each team played against a team from the other group in Round 8, we can surely conclude that the 3rd match of Round 8 must have been played between Team 1 and 4.
Also as per point 2, match ups of Round 5 and Round 8 were identical. Hence we get the details of matches played in Round 5.
Now using information given in points 3, 4, 5 and 6, we will find the details of matches played in various rounds and put the information in a table where alphabet T stands for Team:
From point 6, it is given that Team 3 played Team 8 and Team 2 played Team 5. Clubbing this information with the information in point 1 that each team played against a team from the other group in Round 8, we can surely conclude that the 3rd match of Round 8 must have been played between Team 1 and 4.
Also as per point 2, match ups of Round 5 and Round 8 were identical. Hence we get the details of matches played in Round 5.
Now using information given in points 3, 4, 5 and 6, we will find the details of matches played in various rounds and put the information in a table where alphabet T stands for Team:
 As it is given that every team plays exactly one game in each round, so we can see that T6 would be definitely there in Round 4 and Round 7. Considering the list of matches given for different groups, only T2 is left to play against T6. Hence T2 and T6 would play against each other in Round 4 and 7.
Also match between T2 and T4 is to be played only once. This will be necessarily played in Round 6 as T4 is already playing in Rounds 1, 2 and 3.
Also match between T1 and T2 is to be played twice. This will be necessarily played in Round 1 and Round 3. It means match between T5 and T6 which is to be played only once will be in Round 3.
Also match between T4 and T5 is to be played twice. This will be necessarily played in Round 4 and Round 7. It means match between T1 and T3 which is to be played twice would also be played in Round 4 and Round 7.
So after filling all the above information, we get the final table as follows :
As it is given that every team plays exactly one game in each round, so we can see that T6 would be definitely there in Round 4 and Round 7. Considering the list of matches given for different groups, only T2 is left to play against T6. Hence T2 and T6 would play against each other in Round 4 and 7.
Also match between T2 and T4 is to be played only once. This will be necessarily played in Round 6 as T4 is already playing in Rounds 1, 2 and 3.
Also match between T1 and T2 is to be played twice. This will be necessarily played in Round 1 and Round 3. It means match between T5 and T6 which is to be played only once will be in Round 3.
Also match between T4 and T5 is to be played twice. This will be necessarily played in Round 4 and Round 7. It means match between T1 and T3 which is to be played twice would also be played in Round 4 and Round 7.
So after filling all the above information, we get the final table as follows :
 Now all the questions can be answered.
We can see that Team 5 was not part of the same group as Teams 2,3 and 4. Hence option B.
Now all the questions can be answered.
We can see that Team 5 was not part of the same group as Teams 2,3 and 4. Hence option B.
13. What is the number of the team that played Team 1 in Round 7?
It is given that the 6 teams are divided into two groups containing 3 teams each. As each team in the same group plays every other team once and in the other group twice, so there would be 3 matches among teams of same group and 6 matches among teams of different group. Hence we can find the total matches in the tournament as 3 + 3 + 6 + 6 + 6 = 24.
Also every team plays exactly one game in one round means each round will have 3 matches involving each team. Hence there will be 8 rounds in the tournament.
Now we will further analyse the given information:
As we can see that Team 3 played against Team 6 twice, Team 2 played against Team 5 twice and Team 1 played against Team 4 twice, so Teams 3 & 6, 2 & 5 and 1 & 4 are of different groups.
Now considering points 3 and 4, we get the information that Teams 4 and 6 are of different groups and Teams 1 and 5 are of same group.
Hence we can say that Teams 1, 5 and 6 make a group (say Group I) and correspondingly Teams 2, 3 and 4 (say Group II) make the other group.
So we can list down the matches which will be played among teams of Group I and Group II
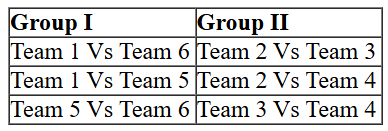 Also we can make a list of matches which were played between teams of different groups:
Also we can make a list of matches which were played between teams of different groups:
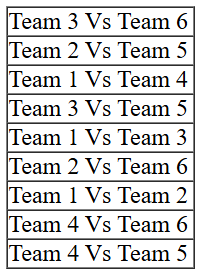 From point 6, it is given that Team 3 played Team 8 and Team 2 played Team 5. Clubbing this information with the information in point 1 that each team played against a team from the other group in Round 8, we can surely conclude that the 3rd match of Round 8 must have been played between Team 1 and 4.
Also as per point 2, match ups of Round 5 and Round 8 were identical. Hence we get the details of matches played in Round 5.
Now using information given in points 3, 4, 5 and 6, we will find the details of matches played in various rounds and put the information in a table where alphabet T stands for Team:
From point 6, it is given that Team 3 played Team 8 and Team 2 played Team 5. Clubbing this information with the information in point 1 that each team played against a team from the other group in Round 8, we can surely conclude that the 3rd match of Round 8 must have been played between Team 1 and 4.
Also as per point 2, match ups of Round 5 and Round 8 were identical. Hence we get the details of matches played in Round 5.
Now using information given in points 3, 4, 5 and 6, we will find the details of matches played in various rounds and put the information in a table where alphabet T stands for Team:
 As it is given that every team plays exactly one game in each round, so we can see that T6 would be definitely there in Round 4 and Round 7. Considering the list of matches given for different groups, only T2 is left to play against T6. Hence T2 and T6 would play against each other in Round 4 and 7.
Also match between T2 and T4 is to be played only once. This will be necessarily played in Round 6 as T4 is already playing in Rounds 1, 2 and 3.
Also match between T1 and T2 is to be played twice. This will be necessarily played in Round 1 and Round 3. It means match between T5 and T6 which is to be played only once will be in Round 3.
Also match between T4 and T5 is to be played twice. This will be necessarily played in Round 4 and Round 7. It means match between T1 and T3 which is to be played twice would also be played in Round 4 and Round 7.
So after filling all the above information, we get the final table as follows :
As it is given that every team plays exactly one game in each round, so we can see that T6 would be definitely there in Round 4 and Round 7. Considering the list of matches given for different groups, only T2 is left to play against T6. Hence T2 and T6 would play against each other in Round 4 and 7.
Also match between T2 and T4 is to be played only once. This will be necessarily played in Round 6 as T4 is already playing in Rounds 1, 2 and 3.
Also match between T1 and T2 is to be played twice. This will be necessarily played in Round 1 and Round 3. It means match between T5 and T6 which is to be played only once will be in Round 3.
Also match between T4 and T5 is to be played twice. This will be necessarily played in Round 4 and Round 7. It means match between T1 and T3 which is to be played twice would also be played in Round 4 and Round 7.
So after filling all the above information, we get the final table as follows :
 Now all the questions can be answered.
As shown, Team 3 played Team 1 in Round 7.
Now all the questions can be answered.
As shown, Team 3 played Team 1 in Round 7.
14. What is the number of the team that played Team 6 in Round 3?
It is given that the 6 teams are divided into two groups containing 3 teams each. As each team in the same group plays every other team once and in the other group twice, so there would be 3 matches among teams of same group and 6 matches among teams of different group. Hence we can find the total matches in the tournament as 3 + 3 + 6 + 6 + 6 = 24.
Also every team plays exactly one game in one round means each round will have 3 matches involving each team. Hence there will be 8 rounds in the tournament.
Now we will further analyse the given information:
As we can see that Team 3 played against Team 6 twice, Team 2 played against Team 5 twice and Team 1 played against Team 4 twice, so Teams 3 & 6, 2 & 5 and 1 & 4 are of different groups.
Now considering points 3 and 4, we get the information that Teams 4 and 6 are of different groups and Teams 1 and 5 are of same group.
Hence we can say that Teams 1, 5 and 6 make a group (say Group I) and correspondingly Teams 2, 3 and 4 (say Group II) make the other group.
So we can list down the matches which will be played among teams of Group I and Group II
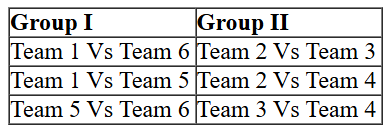 Also we can make a list of matches which were played between teams of different groups::
Also we can make a list of matches which were played between teams of different groups::
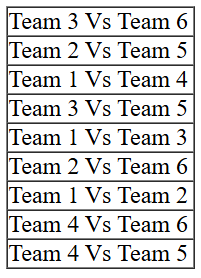 From point 6, it is given that Team 3 played Team 8 and Team 2 played Team 5. Clubbing this information with the information in point 1 that each team played against a team from the other group in Round 8, we can surely conclude that the 3rd match of Round 8 must have been played between Team 1 and 4.
Also as per point 2, match ups of Round 5 and Round 8 were identical. Hence we get the details of matches played in Round 5.
Now using information given in points 3, 4, 5 and 6, we will find the details of matches played in various rounds and put the information in a table where alphabet T stands for Team:
From point 6, it is given that Team 3 played Team 8 and Team 2 played Team 5. Clubbing this information with the information in point 1 that each team played against a team from the other group in Round 8, we can surely conclude that the 3rd match of Round 8 must have been played between Team 1 and 4.
Also as per point 2, match ups of Round 5 and Round 8 were identical. Hence we get the details of matches played in Round 5.
Now using information given in points 3, 4, 5 and 6, we will find the details of matches played in various rounds and put the information in a table where alphabet T stands for Team:
 As it is given that every team plays exactly one game in each round, so we can see that T6 would be definitely there in Round 4 and Round 7. Considering the list of matches given for different groups, only T2 is left to play against T6. Hence T2 and T6 would play against each other in Round 4 and 7.
Also match between T2 and T4 is to be played only once. This will be necessarily played in Round 6 as T4 is already playing in Rounds 1, 2 and 3.
Also match between T1 and T2 is to be played twice. This will be necessarily played in Round 1 and Round 3. It means match between T5 and T6 which is to be played only once will be in Round 3.
Also match between T4 and T5 is to be played twice. This will be necessarily played in Round 4 and Round 7. It means match between T1 and T3 which is to be played twice would also be played in Round 4 and Round 7.
So after filling all the above information, we get the final table as follows :
As it is given that every team plays exactly one game in each round, so we can see that T6 would be definitely there in Round 4 and Round 7. Considering the list of matches given for different groups, only T2 is left to play against T6. Hence T2 and T6 would play against each other in Round 4 and 7.
Also match between T2 and T4 is to be played only once. This will be necessarily played in Round 6 as T4 is already playing in Rounds 1, 2 and 3.
Also match between T1 and T2 is to be played twice. This will be necessarily played in Round 1 and Round 3. It means match between T5 and T6 which is to be played only once will be in Round 3.
Also match between T4 and T5 is to be played twice. This will be necessarily played in Round 4 and Round 7. It means match between T1 and T3 which is to be played twice would also be played in Round 4 and Round 7.
So after filling all the above information, we get the final table as follows :
 Now all the questions can be answered.
As shown, Team 5 played Team 6 in Round 3.
Now all the questions can be answered.
As shown, Team 5 played Team 6 in Round 3.
Correct Answer 10
8
Correct Answer 11
4
Correct Answer 12
Option D
Correct Answer 13
3
Correct Answer 14
5
CAT 2024 | DILR Set 4
Direction Q.15 to 18:
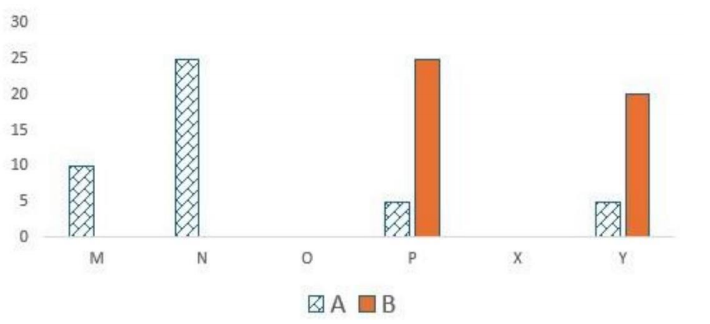
Six web surfers M, N, O, P, X, and Y each had 30 stars which they distributed among four bloggers A, B, C, and D. The number of stars received by A and B from the six web surfers is shown in the figure below.
No. of stars received by Bloggers A and B
The following additional facts are known regarding the number of stars received by the bloggers from the surfers.
- The numbers of stars received by the bloggers from the surfers were all multiples
of 5 (including 0). - The total numbers of stars received by the bloggers were the same.
- Each blogger received a different number of stars from M.
- Two surfers gave all their stars to a single blogger.
- D received more stars than C from Y.
- The numbers of stars received by the bloggers from the surfers were all multiples
15. What was the total number of stars received by D?
It is given that all the six web surfers each had 30 stars. Hence total number of stars = 30 × 6 = 180.
As per the given information and analysing the graph, we can make the initial table::
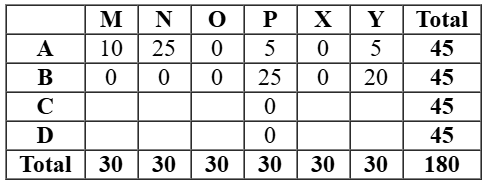 As it is given that the numbers of stars received by the bloggers from the surfers were all multiples of 5 (including 0), so possible values of stars given to the all the bloggers were any of the values 0 or5 or10 or 15 or 25 or 30.
From the 4th point, we can say that the two surfers who gave all their stars to a single blogger must be O and X. Also that blogger is C and D in any order.
As per point 5, D received more stars than C from Y. This tells us that D got 5 stars from Y and C got 0 stars from Y.
As per point 3, C and D could receive 5 and 15 stars from M in any order.
Now let us assume that C received 5 stars from M. So D received 15 stars from M. Hence either O or X gave 30 stars to C. Then N has to give 10 stars to C which is not possible as total stars of N will exceed 30 and total stars of D would exceed 45.
This case is shown below in the table:
As it is given that the numbers of stars received by the bloggers from the surfers were all multiples of 5 (including 0), so possible values of stars given to the all the bloggers were any of the values 0 or5 or10 or 15 or 25 or 30.
From the 4th point, we can say that the two surfers who gave all their stars to a single blogger must be O and X. Also that blogger is C and D in any order.
As per point 5, D received more stars than C from Y. This tells us that D got 5 stars from Y and C got 0 stars from Y.
As per point 3, C and D could receive 5 and 15 stars from M in any order.
Now let us assume that C received 5 stars from M. So D received 15 stars from M. Hence either O or X gave 30 stars to C. Then N has to give 10 stars to C which is not possible as total stars of N will exceed 30 and total stars of D would exceed 45.
This case is shown below in the table:
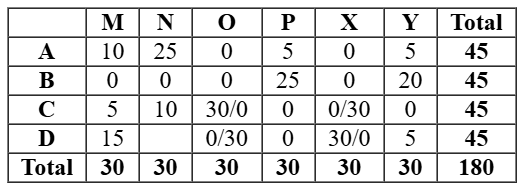 So we will the other case which would be valid in which C received 15 stars from M. So D received 5 stars from M. Hence either O or X gave 30 stars to C and D in any order.
So we get the final table as follows
So we will the other case which would be valid in which C received 15 stars from M. So D received 5 stars from M. Hence either O or X gave 30 stars to C and D in any order.
So we get the final table as follows
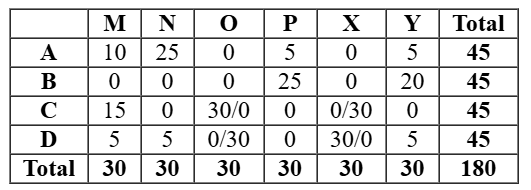 As this table is satisfying all the conditions, so now all the questions can be answered.
As it is given in the information that total number of stars received by the bloggers is the same, so each would receive 180/4 = 45 stars. Hence answer is 45.
As this table is satisfying all the conditions, so now all the questions can be answered.
As it is given in the information that total number of stars received by the bloggers is the same, so each would receive 180/4 = 45 stars. Hence answer is 45.
16. What was the number of stars received by D from Y?
- cannot be determined
- 5
- 0
- 10
It is given that all the six web surfers each had 30 stars. Hence total number of stars = 30 × 6 = 180.
As per the given information and analysing the graph, we can make the initial table:
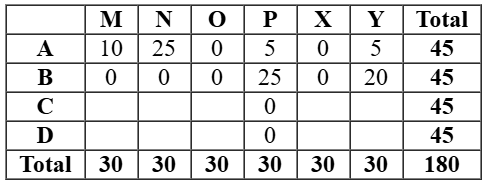 As it is given that the numbers of stars received by the bloggers from the surfers were all multiples of 5 (including 0), so possible values of stars given to the all the bloggers were any of the values 0 or5 or10 or 15 or 25 or 30.
From the 4th point, we can say that the two surfers who gave all their stars to a single blogger must be O and X. Also that blogger is C and D in any order.
As per point 5, D received more stars than C from Y. This tells us that D got 5 stars from Y and C got 0 stars from Y.
As per point 3, C and D could receive 5 and 15 stars from M in any order.
Now let us assume that C received 5 stars from M. So D received 15 stars from M. Hence either O or X gave 30 stars to C. Then N has to give 10 stars to C which is not possible as total stars of N will exceed 30 and total stars of D would exceed 45.
This case is shown below in the table:
As it is given that the numbers of stars received by the bloggers from the surfers were all multiples of 5 (including 0), so possible values of stars given to the all the bloggers were any of the values 0 or5 or10 or 15 or 25 or 30.
From the 4th point, we can say that the two surfers who gave all their stars to a single blogger must be O and X. Also that blogger is C and D in any order.
As per point 5, D received more stars than C from Y. This tells us that D got 5 stars from Y and C got 0 stars from Y.
As per point 3, C and D could receive 5 and 15 stars from M in any order.
Now let us assume that C received 5 stars from M. So D received 15 stars from M. Hence either O or X gave 30 stars to C. Then N has to give 10 stars to C which is not possible as total stars of N will exceed 30 and total stars of D would exceed 45.
This case is shown below in the table:
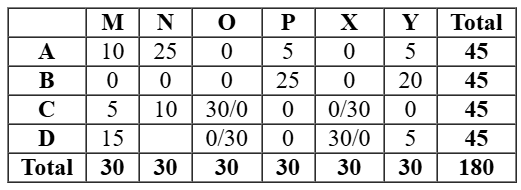 So we will the other case which would be valid in which C received 15 stars from M. So D received 5 stars from M. Hence either O or X gave 30 stars to C and D in any order.
So we get the final table as follows
So we will the other case which would be valid in which C received 15 stars from M. So D received 5 stars from M. Hence either O or X gave 30 stars to C and D in any order.
So we get the final table as follows
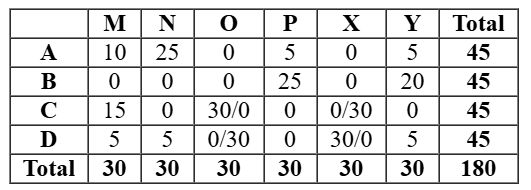 As this table is satisfying all the conditions, so now all the questions can be answered.
As shown in the table, D would receive 5 stars from Y.
As this table is satisfying all the conditions, so now all the questions can be answered.
As shown in the table, D would receive 5 stars from Y.
17. How many surfers distributed their stars among exactly 2 bloggers?
It is given that all the six web surfers each had 30 stars. Hence total number of stars = 30 × 6 = 180.
As per the given information and analysing the graph, we can make the initial table:
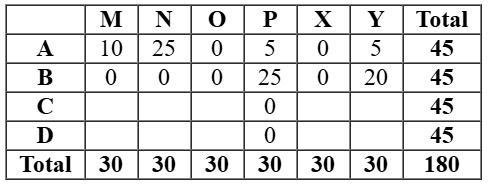 As it is given that the numbers of stars received by the bloggers from the surfers were all multiples of 5 (including 0), so possible values of stars given to the all the bloggers were any of the values 0 or5 or10 or 15 or 25 or 30.
From the 4th point, we can say that the two surfers who gave all their stars to a single blogger must be O and X. Also that blogger is C and D in any order.
As per point 5, D received more stars than C from Y. This tells us that D got 5 stars from Y and C got 0 stars from Y.
As per point 3, C and D could receive 5 and 15 stars from M in any order.
Now let us assume that C received 5 stars from M. So D received 15 stars from M. Hence either O or X gave 30 stars to C. Then N has to give 10 stars to C which is not possible as total stars of N will exceed 30 and total stars of D would exceed 45.
This case is shown below in the table:
As it is given that the numbers of stars received by the bloggers from the surfers were all multiples of 5 (including 0), so possible values of stars given to the all the bloggers were any of the values 0 or5 or10 or 15 or 25 or 30.
From the 4th point, we can say that the two surfers who gave all their stars to a single blogger must be O and X. Also that blogger is C and D in any order.
As per point 5, D received more stars than C from Y. This tells us that D got 5 stars from Y and C got 0 stars from Y.
As per point 3, C and D could receive 5 and 15 stars from M in any order.
Now let us assume that C received 5 stars from M. So D received 15 stars from M. Hence either O or X gave 30 stars to C. Then N has to give 10 stars to C which is not possible as total stars of N will exceed 30 and total stars of D would exceed 45.
This case is shown below in the table: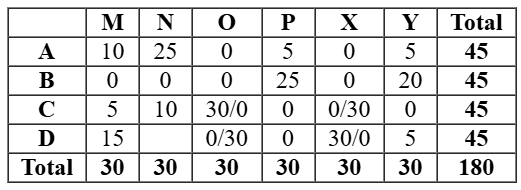 So we will the other case which would be valid in which C received 15 stars from M. So D received 5 stars from M. Hence either O or X gave 30 stars to C and D in any order.
So we get the final table as follows
So we will the other case which would be valid in which C received 15 stars from M. So D received 5 stars from M. Hence either O or X gave 30 stars to C and D in any order.
So we get the final table as follows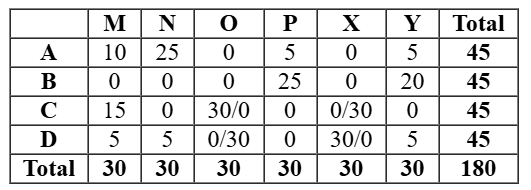 As this table is satisfying all the conditions, so now all the questions can be answered.
From the table, we can infer that 2 surfers N and P distributed their stars among exactly 2 bloggers. (N distributed his stars to A and D only and P distributed his stars to A and B only.
As this table is satisfying all the conditions, so now all the questions can be answered.
From the table, we can infer that 2 surfers N and P distributed their stars among exactly 2 bloggers. (N distributed his stars to A and D only and P distributed his stars to A and B only.
18. Which of the following can be determined with certainty?
I. The number of stars received by C from M
II. The number of stars received by 𝐷 from 𝑂
- Only I
- Both I and II
- Only II
- Neither I nor II
It is given that all the six web surfers each had 30 stars. Hence total number of stars = 30 × 6 = 180.
As per the given information and analysing the graph, we can make the initial table: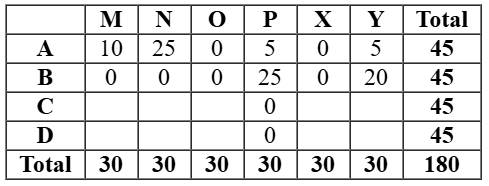 As it is given that the numbers of stars received by the bloggers from the surfers were all multiples of 5 (including 0), so possible values of stars given to the all the bloggers were any of the values 0 or5 or10 or 15 or 25 or 30.
From the 4th point, we can say that the two surfers who gave all their stars to a single blogger must be O and X. Also that blogger is C and D in any order.
As per point 5, D received more stars than C from Y. This tells us that D got 5 stars from Y and C got 0 stars from Y.
As per point 3, C and D could receive 5 and 15 stars from M in any order.
Now let us assume that C received 5 stars from M. So D received 15 stars from M. Hence either O or X gave 30 stars to C. Then N has to give 10 stars to C which is not possible as total stars of N will exceed 30 and total stars of D would exceed 45.
This case is shown below in the table:
As it is given that the numbers of stars received by the bloggers from the surfers were all multiples of 5 (including 0), so possible values of stars given to the all the bloggers were any of the values 0 or5 or10 or 15 or 25 or 30.
From the 4th point, we can say that the two surfers who gave all their stars to a single blogger must be O and X. Also that blogger is C and D in any order.
As per point 5, D received more stars than C from Y. This tells us that D got 5 stars from Y and C got 0 stars from Y.
As per point 3, C and D could receive 5 and 15 stars from M in any order.
Now let us assume that C received 5 stars from M. So D received 15 stars from M. Hence either O or X gave 30 stars to C. Then N has to give 10 stars to C which is not possible as total stars of N will exceed 30 and total stars of D would exceed 45.
This case is shown below in the table: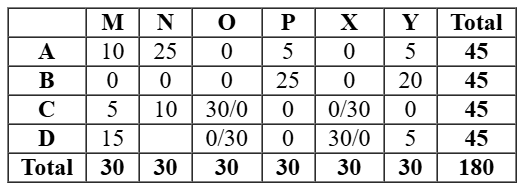 So we will the other case which would be valid in which C received 15 stars from M. So D received 5 stars from M. Hence either O or X gave 30 stars to C and D in any order.
So we get the final table as follows
So we will the other case which would be valid in which C received 15 stars from M. So D received 5 stars from M. Hence either O or X gave 30 stars to C and D in any order.
So we get the final table as follows
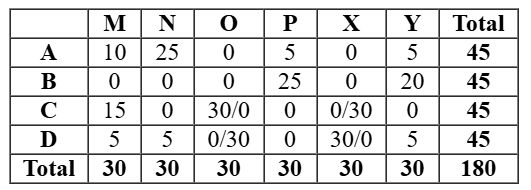 As this table is satisfying all the conditions, so now all the questions can be answered.
As shown in the table, the number of stars received by C from M can be uniquely determined as 15. But we cannot determine the number of stars received by D from O. They could be either 0 or 30.
As this table is satisfying all the conditions, so now all the questions can be answered.
As shown in the table, the number of stars received by C from M can be uniquely determined as 15. But we cannot determine the number of stars received by D from O. They could be either 0 or 30.
Correct Answer 15
45
Correct Answer 16
Option B
Correct Answer 17
2
Correct Answer 18
Option A
CAT 2024 | DILR Set 5
Direction Q.19 to 22:
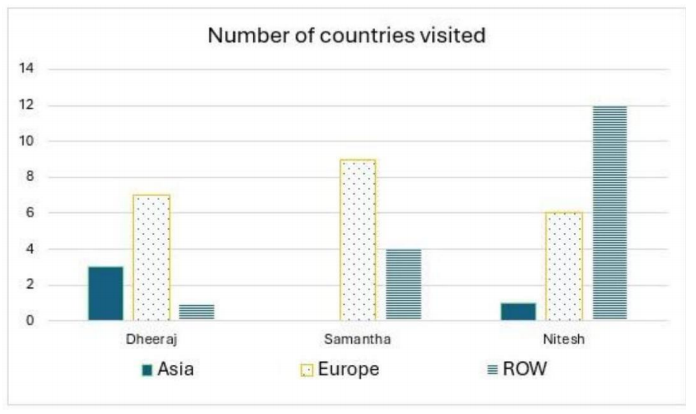
The following additional facts are known about the countries visited by them.
- 32 countries were visited by at least one of them.
- USA (in ROW) is the only country that was visited by all three of them
- China (in Asia) is the only country that was visited by both Dheeraj and Nitesh, but not by Samantha.
- France (in Europe) is the only country outside Asia, which was visited by both Dheeraj and Samantha, but not by Nitesh.
- Half of the countries visited by both Samantha and Nitesh are in Europe.
19. How many countries in Asia were visited by at least one of Dheeraj, Samantha and Nitesh?
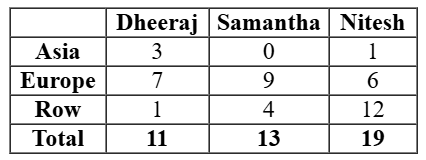
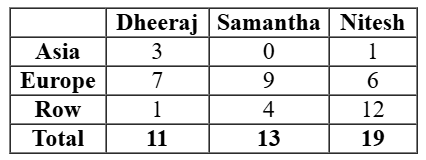
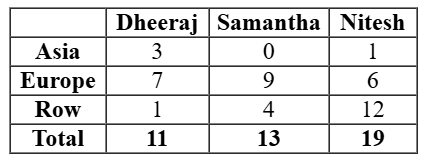
As per the bar graph given in the question, we can make a table of number of countries visited by the 3 people:
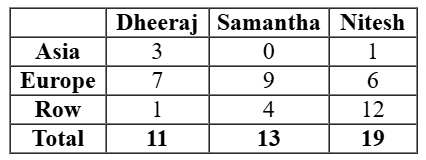 Now we can make Venn Diagram of all the information given and solving the equations to get the values of various variables.
Now we can make Venn Diagram of all the information given and solving the equations to get the values of various variables.
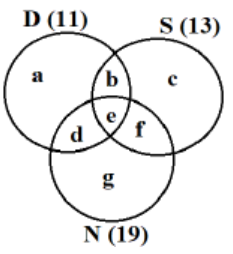 As it is given that 32 countries were visited by at least one of them, we get the equations as
a + b + c + d + e + f + g = 32……….(1)
a + c + g + 2(b + d + f) + 3e = 43….(2)
a + b + d + e = 11
b + c + e + f = 13
d + e + f + g = 19
As per point 2, USA is the only country that was visited by all three of them, so values of e = 1
As per point 3, China is the only country that was visited by both Dheeraj and Nitesh, but not by Samantha, so d = 1.
As per point 4, France is the only country outside Asia, which was visited by both Dheeraj and Samantha, but not by Nitesh, so b = 1.
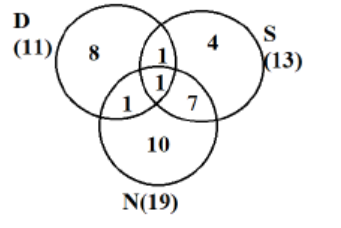
As a + b + d + e = 11, so a + 1 + 1 + 1 = 11, so a = 8
Also number of people visiting exactly 3 countries = 1
(2) – (1) gives us b +d + f + 2e = 11. Putting e = 1 gives b + d + f = 9
Hence number of people visiting exactly 2 countries = 9
Since total given is 32, so Exactly 1 + Exactly 2 + Exactly 3 = 32
So number of people visiting exactly 1 countries= 32 – 1 – 9 = 22
As it is given that 32 countries were visited by at least one of them, we get the equations as
a + b + c + d + e + f + g = 32……….(1)
a + c + g + 2(b + d + f) + 3e = 43….(2)
a + b + d + e = 11
b + c + e + f = 13
d + e + f + g = 19
As per point 2, USA is the only country that was visited by all three of them, so values of e = 1
As per point 3, China is the only country that was visited by both Dheeraj and Nitesh, but not by Samantha, so d = 1.
As per point 4, France is the only country outside Asia, which was visited by both Dheeraj and Samantha, but not by Nitesh, so b = 1.
As a + b + d + e = 11, so a + 1 + 1 + 1 = 11, so a = 8
Also number of people visiting exactly 3 countries = 1
(2) – (1) gives us b +d + f + 2e = 11. Putting e = 1 gives b + d + f = 9
Hence number of people visiting exactly 2 countries = 9
Since total given is 32, so Exactly 1 + Exactly 2 + Exactly 3 = 32
So number of people visiting exactly 1 countries= 32 – 1 – 9 = 22
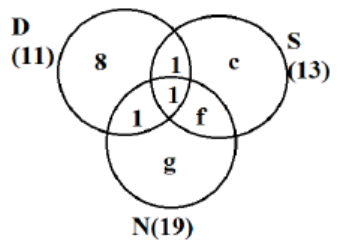
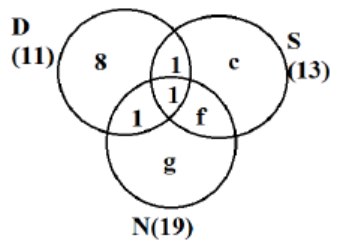
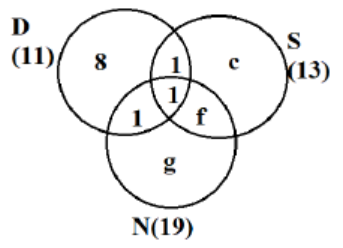 As exactly 2 = 9, so 1 + 1 + f = 9
Þ f = 7
Also b + c + e + f = 13
Þ 1 + c + 1 + 7 = 13
Þ c = 4
As number of people visiting exactly 1 countries is 22, so 8 + c + g = 22
Þ 8 + 4 + g = 22
Þ g = 10
So we can make the final Venn Diagram as follows
As exactly 2 = 9, so 1 + 1 + f = 9
Þ f = 7
Also b + c + e + f = 13
Þ 1 + c + 1 + 7 = 13
Þ c = 4
As number of people visiting exactly 1 countries is 22, so 8 + c + g = 22
Þ 8 + 4 + g = 22
Þ g = 10
So we can make the final Venn Diagram as follows
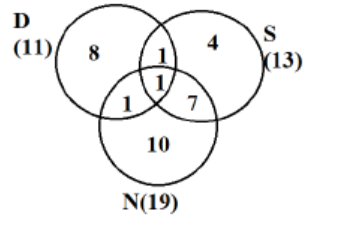
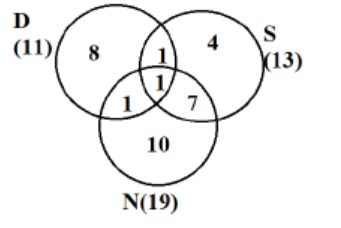
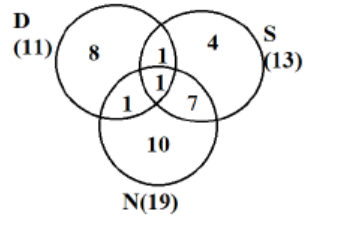 Now we need to make a final table of countries visited by these 3 people in various domains given::
Now we need to make a final table of countries visited by these 3 people in various domains given::
 As per point 5, half of the countries visited by both Samantha and Nitesh are in Europe, so number of countries visited by Samantha and Nitesh alone would be (7+1)2 = 4.
Now we can answer all the questions:
As shown in the table above, 3 countries in Asia were visited by at least one of Dheeraj, Samantha and Nitesh.
As per point 5, half of the countries visited by both Samantha and Nitesh are in Europe, so number of countries visited by Samantha and Nitesh alone would be (7+1)2 = 4.
Now we can answer all the questions:
As shown in the table above, 3 countries in Asia were visited by at least one of Dheeraj, Samantha and Nitesh.
20. How many countries in Europe were visited only by Nitesh?
As per the bar graph given in the question, we can make a table of number of countries visited by the 3 people:
 Now we can make Venn Diagram of all the information given and solving the equations to get the values of various variables.
Now we can make Venn Diagram of all the information given and solving the equations to get the values of various variables.
 As it is given that 32 countries were visited by at least one of them, we get the equations as
a + b + c + d + e + f + g = 32……….(1)
a + c + g + 2(b + d + f) + 3e = 43….(2)
a + b + d + e = 11
b + c + e + f = 13
d + e + f + g = 19
As per point 2, USA is the only country that was visited by all three of them, so values of e = 1
As per point 3, China is the only country that was visited by both Dheeraj and Nitesh, but not by Samantha, so d = 1.
As per point 4, France is the only country outside Asia, which was visited by both Dheeraj and Samantha, but not by Nitesh, so b = 1.
As a + b + d + e = 11, so a + 1 + 1 + 1 = 11, so a = 8
Also number of people visiting exactly 3 countries = 1
(2) – (1) gives us b +d + f + 2e = 11. Putting e = 1 gives b + d + f = 9
Hence number of people visiting exactly 2 countries = 9
Since total given is 32, so Exactly 1 + Exactly 2 + Exactly 3 = 32
So number of people visiting exactly 1 countries= 32 – 1 – 9 = 22
As it is given that 32 countries were visited by at least one of them, we get the equations as
a + b + c + d + e + f + g = 32……….(1)
a + c + g + 2(b + d + f) + 3e = 43….(2)
a + b + d + e = 11
b + c + e + f = 13
d + e + f + g = 19
As per point 2, USA is the only country that was visited by all three of them, so values of e = 1
As per point 3, China is the only country that was visited by both Dheeraj and Nitesh, but not by Samantha, so d = 1.
As per point 4, France is the only country outside Asia, which was visited by both Dheeraj and Samantha, but not by Nitesh, so b = 1.
As a + b + d + e = 11, so a + 1 + 1 + 1 = 11, so a = 8
Also number of people visiting exactly 3 countries = 1
(2) – (1) gives us b +d + f + 2e = 11. Putting e = 1 gives b + d + f = 9
Hence number of people visiting exactly 2 countries = 9
Since total given is 32, so Exactly 1 + Exactly 2 + Exactly 3 = 32
So number of people visiting exactly 1 countries= 32 – 1 – 9 = 22
 As exactly 2 = 9, so 1 + 1 + f = 9
Þ f = 7
Also b + c + e + f = 13
Þ 1 + c + 1 + 7 = 13
Þ c = 4
As number of people visiting exactly 1 countries is 22, so 8 + c + g = 22
Þ 8 + 4 + g = 22
Þ g = 10
So we can make the final Venn Diagram as follows
As exactly 2 = 9, so 1 + 1 + f = 9
Þ f = 7
Also b + c + e + f = 13
Þ 1 + c + 1 + 7 = 13
Þ c = 4
As number of people visiting exactly 1 countries is 22, so 8 + c + g = 22
Þ 8 + 4 + g = 22
Þ g = 10
So we can make the final Venn Diagram as follows
 Now we need to make a final table of countries visited by these 3 people in various domains given::
Now we need to make a final table of countries visited by these 3 people in various domains given::
 As per point 5, half of the countries visited by both Samantha and Nitesh are in Europe, so number of countries visited by Samantha and Nitesh alone would be (7+1)2 = 4.
Now we can answer all the questions:
As shown in the table above, Nitesh visited 2 countries in Europe alone.
As per point 5, half of the countries visited by both Samantha and Nitesh are in Europe, so number of countries visited by Samantha and Nitesh alone would be (7+1)2 = 4.
Now we can answer all the questions:
As shown in the table above, Nitesh visited 2 countries in Europe alone.
21. How many countries in the ROW were visited by both Nitesh and Samantha?
As per the bar graph given in the question, we can make a table of number of countries visited by the 3 people:
 Now we can make Venn Diagram of all the information given and solving the equations to get the values of various variables.
Now we can make Venn Diagram of all the information given and solving the equations to get the values of various variables.
 As it is given that 32 countries were visited by at least one of them, we get the equations as
a + b + c + d + e + f + g = 32……….(1)
a + c + g + 2(b + d + f) + 3e = 43….(2)
a + b + d + e = 11
b + c + e + f = 13
d + e + f + g = 19
As per point 2, USA is the only country that was visited by all three of them, so values of e = 1
As per point 3, China is the only country that was visited by both Dheeraj and Nitesh, but not by Samantha, so d = 1.
As per point 4, France is the only country outside Asia, which was visited by both Dheeraj and Samantha, but not by Nitesh, so b = 1.
As a + b + d + e = 11, so a + 1 + 1 + 1 = 11, so a = 8
Also number of people visiting exactly 3 countries = 1
(2) – (1) gives us b +d + f + 2e = 11. Putting e = 1 gives b + d + f = 9
Hence number of people visiting exactly 2 countries = 9
Since total given is 32, so Exactly 1 + Exactly 2 + Exactly 3 = 32
So number of people visiting exactly 1 countries= 32 – 1 – 9 = 22
As it is given that 32 countries were visited by at least one of them, we get the equations as
a + b + c + d + e + f + g = 32……….(1)
a + c + g + 2(b + d + f) + 3e = 43….(2)
a + b + d + e = 11
b + c + e + f = 13
d + e + f + g = 19
As per point 2, USA is the only country that was visited by all three of them, so values of e = 1
As per point 3, China is the only country that was visited by both Dheeraj and Nitesh, but not by Samantha, so d = 1.
As per point 4, France is the only country outside Asia, which was visited by both Dheeraj and Samantha, but not by Nitesh, so b = 1.
As a + b + d + e = 11, so a + 1 + 1 + 1 = 11, so a = 8
Also number of people visiting exactly 3 countries = 1
(2) – (1) gives us b +d + f + 2e = 11. Putting e = 1 gives b + d + f = 9
Hence number of people visiting exactly 2 countries = 9
Since total given is 32, so Exactly 1 + Exactly 2 + Exactly 3 = 32
So number of people visiting exactly 1 countries= 32 – 1 – 9 = 22
 As exactly 2 = 9, so 1 + 1 + f = 9
Þ f = 7
Also b + c + e + f = 13
Þ 1 + c + 1 + 7 = 13
Þ c = 4
As number of people visiting exactly 1 countries is 22, so 8 + c + g = 22
Þ 8 + 4 + g = 22
Þ g = 10
So we can make the final Venn Diagram as follows
As exactly 2 = 9, so 1 + 1 + f = 9
Þ f = 7
Also b + c + e + f = 13
Þ 1 + c + 1 + 7 = 13
Þ c = 4
As number of people visiting exactly 1 countries is 22, so 8 + c + g = 22
Þ 8 + 4 + g = 22
Þ g = 10
So we can make the final Venn Diagram as follows
 Now we need to make a final table of countries visited by these 3 people in various domains given::
Now we need to make a final table of countries visited by these 3 people in various domains given::
 As per point 5, half of the countries visited by both Samantha and Nitesh are in Europe, so number of countries visited by Samantha and Nitesh alone would be (7+1)2 = 4.
Now we can answer all the questions:
As shown in the table above, 3 + 1 = 4 countries in ROW were visited by both Nitesh and Samantha.
As per point 5, half of the countries visited by both Samantha and Nitesh are in Europe, so number of countries visited by Samantha and Nitesh alone would be (7+1)2 = 4.
Now we can answer all the questions:
As shown in the table above, 3 + 1 = 4 countries in ROW were visited by both Nitesh and Samantha.
22. How many countries in Europe were visited by exactly one of Dheeraj, Samantha and Nitesh?
- 10
- 12
- 5
- 14
As per the bar graph given in the question, we can make a table of number of countries visited by the 3 people:
 Now we can make Venn Diagram of all the information given and solving the equations to get the values of various variables.
Now we can make Venn Diagram of all the information given and solving the equations to get the values of various variables.
 As it is given that 32 countries were visited by at least one of them, we get the equations as
a + b + c + d + e + f + g = 32……….(1)
a + c + g + 2(b + d + f) + 3e = 43….(2)
a + b + d + e = 11
b + c + e + f = 13
d + e + f + g = 19
As per point 2, USA is the only country that was visited by all three of them, so values of e = 1
As per point 3, China is the only country that was visited by both Dheeraj and Nitesh, but not by Samantha, so d = 1.
As per point 4, France is the only country outside Asia, which was visited by both Dheeraj and Samantha, but not by Nitesh, so b = 1.
As a + b + d + e = 11, so a + 1 + 1 + 1 = 11, so a = 8
Also number of people visiting exactly 3 countries = 1
(2) – (1) gives us b +d + f + 2e = 11. Putting e = 1 gives b + d + f = 9
Hence number of people visiting exactly 2 countries = 9
Since total given is 32, so Exactly 1 + Exactly 2 + Exactly 3 = 32
So number of people visiting exactly 1 countries= 32 – 1 – 9 = 22
As it is given that 32 countries were visited by at least one of them, we get the equations as
a + b + c + d + e + f + g = 32……….(1)
a + c + g + 2(b + d + f) + 3e = 43….(2)
a + b + d + e = 11
b + c + e + f = 13
d + e + f + g = 19
As per point 2, USA is the only country that was visited by all three of them, so values of e = 1
As per point 3, China is the only country that was visited by both Dheeraj and Nitesh, but not by Samantha, so d = 1.
As per point 4, France is the only country outside Asia, which was visited by both Dheeraj and Samantha, but not by Nitesh, so b = 1.
As a + b + d + e = 11, so a + 1 + 1 + 1 = 11, so a = 8
Also number of people visiting exactly 3 countries = 1
(2) – (1) gives us b +d + f + 2e = 11. Putting e = 1 gives b + d + f = 9
Hence number of people visiting exactly 2 countries = 9
Since total given is 32, so Exactly 1 + Exactly 2 + Exactly 3 = 32
So number of people visiting exactly 1 countries= 32 – 1 – 9 = 22
 As exactly 2 = 9, so 1 + 1 + f = 9
Þ f = 7
Also b + c + e + f = 13
Þ 1 + c + 1 + 7 = 13
Þ c = 4
As number of people visiting exactly 1 countries is 22, so 8 + c + g = 22
Þ 8 + 4 + g = 22
Þ g = 10
So we can make the final Venn Diagram as follows
As exactly 2 = 9, so 1 + 1 + f = 9
Þ f = 7
Also b + c + e + f = 13
Þ 1 + c + 1 + 7 = 13
Þ c = 4
As number of people visiting exactly 1 countries is 22, so 8 + c + g = 22
Þ 8 + 4 + g = 22
Þ g = 10
So we can make the final Venn Diagram as follows
 Now we need to make a final table of countries visited by these 3 people in various domains given::
Now we need to make a final table of countries visited by these 3 people in various domains given::
 As per point 5, half of the countries visited by both Samantha and Nitesh are in Europe, so number of countries visited by Samantha and Nitesh alone would be (7+1)2 = 4.
Now we can answer all the questions:
As shown in the table above, 6 + 4 + 2 = 12 countries in Europe were visited by exactly one of Dheeraj, Samantha and Nitesh. Hence option C.
As per point 5, half of the countries visited by both Samantha and Nitesh are in Europe, so number of countries visited by Samantha and Nitesh alone would be (7+1)2 = 4.
Now we can answer all the questions:
As shown in the table above, 6 + 4 + 2 = 12 countries in Europe were visited by exactly one of Dheeraj, Samantha and Nitesh. Hence option C.
Correct Answer 19
3
Correct Answer 20
2
Correct Answer 21
4
Correct Answer 22
Option B