Let f(x) be quadratic polynomial in x such that f (x) ≥ 0 for all real numbers x. if f(2) = 0 and f(4) = 6, then f(-2) is equal to
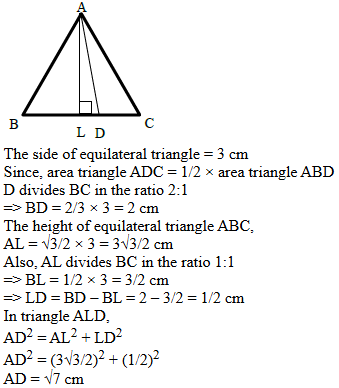
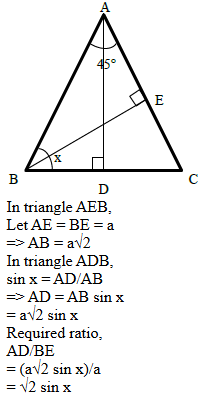
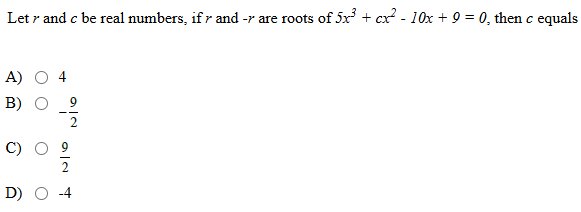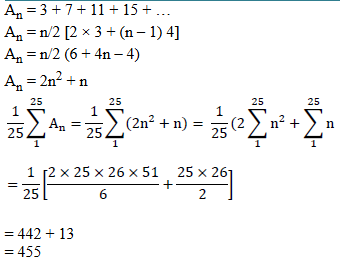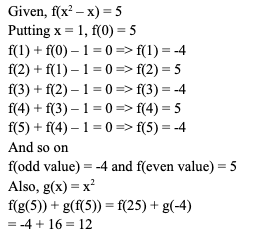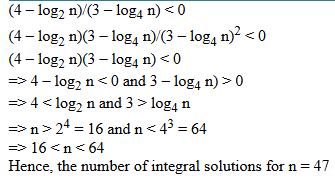Since, f(x) ≥ 0 and f(2) = 0 => Both the roots of the quadratic polynomial are equal to 2 Let the quadratic polynomial be f(x) = ax2 + bx + c Sum of roots = 2 + 2 = -b/a => b = -4a Product of roots = 2 × 2 = c/a => c = 4a Also, f(4) = 6 => 16a + 4b + c = 6 Substituting and solving, 16a + 4 (-4a) + 4a = 6 => a = 1.5, b = -6 and c = 6 f(-2) = 1.5 (-2)2 + (-6)(-2) + 6 = 24
Manu earns Rs. 4000 per month and wants to save an average of Rs. 550 per month in a year. In the first nine months, his monthly expense was Rs. 3500, and he foresees that, tenth month onward, his monthly expense will increase to Rs. 3700. In order to meet his yearly savings target, his monthly earnings, in rupees, from the tenth month onward should be
Total income of Manu for 1st nine months = 4000 × 9 = Rs 36000 Total expenditure for 1st nine months = 3500 × 9 = Rs 31500 Total savings for the 1st nine months = 36000 – 31500 = Rs 4500 Total annual saving = 550 × 12 = Rs 6600 Total saving for the last three months = 6600 – 4500 = Rs 2100 Total expenditure for the last three months = 3700 × 3 = Rs 11100 Total income for the last three months = 2100 + 11100 = Rs 13200 Income per month for the remaining 3 months = 13200/3 = Rs 4400
Working alone, the times taken by Anu, Tanu and Manu to complete any job are in the ratio 5 : 8 : 10. They accept a job which they can finish in 4 days if they all work together for 8 hours per day. However, Anu and Tanu work together for the first 6 days, working 6 hours 40 minutes per day. Then, the number of hours that Manu will take to complete the remaining job working alone is (in numerical value only)
Time taken by Anu = 5t, Tanu = 8t and Manu = 10t (where t is in hours) Let job = 40t (LCM of 5t, 8t and 10t) Efficiency of Anu, A = 8 units/hour Efficiency of Tanu, T = 5 units/hour Efficiency of Manu, M = 4 units/hour A + T + M = 40t/(4 × 8) Solving, total job = 40t = 544 units Job done by Anu and Tanu in 6 days working 6 hrs 40 mins (= 20/3 hrs) = (8 + 5) × 6 × 20/3 = 520 units Remaining job = 544 – 520 = 24 units Time taken by Manu to complete the remaining job = 24/4 = 6 hours
Five students, including Amit, appear for an examination in which possible marks are integers between 0 and 50, both inclusive. The average marks for all the students is 38 and exactly three students got more than 32. If no two students got the same marks and Amit got the least marks among the five students, then the difference between the highest and lowest possible marks of Amit is
Let the marks scored by Amit be A and by other candidates be B, C, D and E Given, A + B + C + D + E = 38 × 5 = 190 Exactly three of them scored above 32 and no two student scored same marks Lowest marks scored by Amit, when rest scored the maximum Let B = 32, C = 48, D = 49 and E = 50 => Lowest marks scored by Amit = 190 – (32 + 48 + 49 + 50) = 11 Highest marks scored by Amit = 31 such that B = 32, C + D + E = 190 – (31 + 32) = 127 Required difference = 31 – 11 = 20
In an examination, there were 75 questions. 3 marks were awarded for each correct answer, 1 mark was deducted for each wrong answer and 1 mark was awarded for each unattempted question. Rayan scored a total of 97 marks in the examination. If the number of unattempted questions was higher than the number of attempted questions, then the maximum number of correct answers that Rayan could have given in the examination is (in numerical value only)
Let the number of correct answered questions = x, wrong = y and unattempted = z Given, x + y + z = 75 Also, 3x – y + z = 97 Subtracting, 2x – 2y = 22 => x – y = 11 Also, z > x + y => x + y (maximum) = 37 (such that z = 38) => 2x = 48 (maximum) => x = 24 (maximum)
There are two containers of the same volume, first container half-filled with sugar syrup and the second container half-filled with milk. Half the content of the first container is transferred to the second container, and then the half of this mixture is transferred back to the first container. Next, half the content of the first container is transferred back to the second container. Then the ratio of sugar syrup and milk in the second container is
Two ships meet mid-ocean, and then, one ship goes south and the other ship goes west, both travelling at constant speeds. Two hours later, they are 60 km apart. If the speed of one of the ships is 6 km per hour more than the other one, then the speed, in km per hour, of the slower ship is
The number of integers greater than 2000 that can be formed with the digits 0, 1, 2, 3, 4, 5, using each digit at most once, is
Number of integers > 2000 are 4 digit numbers = 4 × 5 × 4 × 3 = 240 5 digit numbers = 5 × 5 × 4 × 3 × 2 = 600 6 digit numbers = 5 × 5 × 4 × 3 × 2 × 1 = 600 Total = 240 + 600 + 600 = 1440
Let the third root of the cubic equation f(x) = 5x3 + cx2 – 10x + 9 = 0 is p Sum of roots = r – r + p = -c/5 => p = -c/5 Sum of roots taken two at a time = r(-r) + rp + (-r)p = -10/5 = -2 => -r2 = -2 => r = ±√2 Product of roots = r (-r) p = -9/5 => p = 9/10 Substituting and solving, 9/10 = -c/5 => c = -9/2
On day one, there are 100 particles in laboratory experiment. On day n, where n ≥ 2, one out of every n particles produces another particle. If the total number of particles in the laboratory experiment increases to 1000 on day m, then m equals.
Day 1, number of bacteria = 100 Day 2, 1/2 × 100 = 50 more bacteria produces, total = 150 Day 3, 1/3 × 150 = 50 more bacteria produces, total = 200 Day 4, 1/4 × 200 = 50 more bacteria produces, total = 250 And so on This forms an AP with 1st term as 100 and common difference = 50 Let the required day = dth day Solving, 100 + (d – 1) 50 ≥ 1000 => (d – 1) ≥ 18 => d ≥ 19 Hence, on 19th day, the total number of bacteria will be more than or equal to 1000
In an election, there were four candidates and 80% of the registered voters casted their votes. One of the candidates received 30% of the casted votes while the other three candidates received the remaining casted votes in the proportion 1 : 2 : 3. If the winner of the election received 2512 votes more than the candidate with the second highest votes, then the number of registered voters was
Let the total number of registered voters = 300x => total number of votes casted = 240x Number of votes one candidate received = 30% of 240x = 72x Remaining votes = 240x – 72x = 168x Number of votes received by other three candidates 1/6 × 168x = 28x, 2/6 × 168x = 56x and 3/6 × 168x = 84x Given, 84x – 72x = 2512 => 12x = 2512 => 300x = 62800
Pinto invests one-fifth of his capital at 6%, one-third at 10% and the remaining at 1%, each rate being simple interest per annum. Then, the minimum number of years required for the cumulative interest income from these investments to equal or exceed his initial capital is (in numerical value only)
Let total investment by Mr. Pinto = 15P 1/5 × 15P = 3P at 6% SI 1/3 × 15P = 5P at 10% SI Remaining, 15P – (3P + 5P) = 7P at 1% SI Let the required number of years = t Total simple interest = (3P × 6/100 + 5P × 10/100 + 7P × 1/100) × t ≥ 15P Solving, 75P/100 × t ≥ 15P => t ≥ 20 Hence, the minimum number of years = 20 years
If a and b are non-negative real numbers such that a + 2b = 6, then the average of the maximum and minimum possible values of (a + b) is
Given, a + 2b = 6 where a and b are non-negative real numbers The maximum value of a + b = 6 when a = 6 and b = 0 And the minimum value of a + b = 3 when a = 0 and b = 3 Hence, the required average = (6 + 3)/2 = 4.5
We at Quantifiers understand and deliver on the personal attention each of our students requires. Whether it is through our pedagogy that enables non-engineers or non-math background students, our constant effort to proactively provide solutions, or our focus on our student’s goals.
