CAT 2023 | DILR Set 1
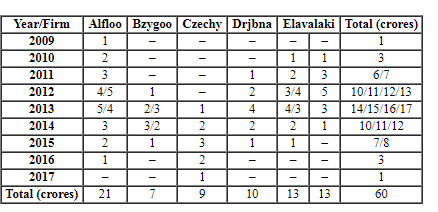
Odsville has five firms – Alfloo, Bzygoo, Czechy, Drjbna and Elavalaki. Each of these firms was founded in some year and also closed down a few years later.
Each firm raised Rs. 1 crore in its first and last year of existence. The amount each firm raised every year increased until it reached a maximum, and then decreased until the firm closed down. No firm raised the same amount of money in two consecutive years. Each annual increase and decrease was either by Rs. 1 crore or by Rs. 2 crores.
The table below provides partial information about the five firms.
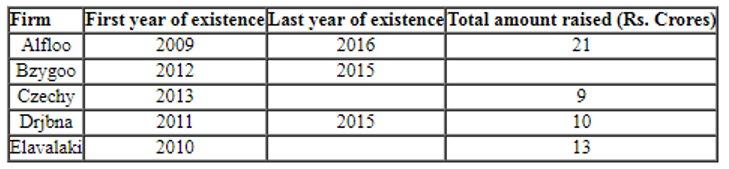
1. For which firm(s) can the amounts raised by them be concluded with certainty in each year?
- Only Drjbna
- Only Czechy
- Only Czechy and Drjbna
- Only Bzygoo and Czechy and Drjbna
Given that each firm raised Rs 1 crore in its first and last year. Also, each annual increase and decrease was either of Rs 1 crore or by Rs 2 crores.
Let us consider for Alfloo,
First year of existence, 2009 = Rs 1 crore = Last year of existence, 2016
Let amount raised in 2010, 2011, 2012, 2013, 2014, 2015 be a, b, c, d, e and f respectively
Solving, 1 + a + b + c + d + e + f + 1 = 21
⇒ a + b + c + d + e + f = 19
Now, even if we consider minimum annual increase and decrease annually,
The values can be a = 2, b = 3, c = 4 or 5, d = 5 or 4, e = 3 and f = 2
Now for Bzygoo,
First year of existence, 2012 = Rs 1 crore = Last year of existence, 2015
The possibilities for the amount raised in 2013 = 2 or 3 and in 2014 = 3 or 2 respectively
Thus the total amount raised by Bzygoo = Rs 7 crores
Now for Czechy,
First year of existence, 2013 = Rs 1 crore
Total amount raised = Rs 9 crores
Now, if we consider Year 2016 as the last year of existence
The possible values of amount raised for
Year 2014 = 2 or 3, Year 2015 = 3 or 2 and Year 2016 = 1
The possible sum = Rs 7 crores (maximum)
So, the last year of existence for the firm Czechy has to be 2017 with only possible values
Year 2013 = 1, Year 2014 = 2, Year 2015 = 3, Year 2016 = 2 and Year 2017 = 1
Thus, the total amount raised = Rs 9 crores
Now for Drjbna,
First year of existence, 2011 = Rs 1 crore = Last year of existence, 2015
Total amount raised = Rs 10 crores
The only possible value of amount raised for
Year 2012 = 2, Year 2013 = 4 and Year 2014 = 2
Now for Elavalaki,
Total amount raised = Rs 13 crores
First year of existence, 2011 = Rs 1 crore but last year of existence is not given
Considering the minimum amounts the possible values of amount raised for
Year 2010 = 1, Year 2011 = 2, Year 2012 = 3 or 4, Year 2013 = 4 or 3, Year 2014 = 2 and Year 2015 = 1 (such that Year 2015 is the last year of existence)
Considering the maximum amounts the possible values of amount raised for
Year 2010 = 1, Year 2011 = 3, Year 2012 = 5, Year 2013 = 3, Year 2014 = 1 (such that Year 2014 is the last year of existence)
The rest of the information can be gathered as follows-
The amount raised by only firms Czechy and Drjbna can be concluded with certainty in each year.
2. What best can be concluded about the total amount of money raised in 2015?
- It is either Rs. 8 crores or Rs. 9 crores.
- It is exactly Rs. 8 crores.
- It is either Rs. 7 crores or Rs. 8 crores or Rs. 9 crores.
- It is either Rs. 7 crores or Rs. 8 crores.
Given that each firm raised Rs 1 crore in its first and last year. Also, each annual increase and decrease was either of Rs 1 crore or by Rs 2 crores.
Let us consider for Alfloo,
First year of existence, 2009 = Rs 1 crore = Last year of existence, 2016
Let amount raised in 2010, 2011, 2012, 2013, 2014, 2015 be a, b, c, d, e and f respectively
Solving, 1 + a + b + c + d + e + f + 1 = 21
⇒ a + b + c + d + e + f = 19
Now, even if we consider minimum annual increase and decrease annually,
The values can be a = 2, b = 3, c = 4 or 5, d = 5 or 4, e = 3 and f = 2
Now for Bzygoo,
First year of existence, 2012 = Rs 1 crore = Last year of existence, 2015
The possibilities for the amount raised in 2013 = 2 or 3 and in 2014 = 3 or 2 respectively
Thus the total amount raised by Bzygoo = Rs 7 crores
Now for Czechy,
First year of existence, 2013 = Rs 1 crore
Total amount raised = Rs 9 crores
Now, if we consider Year 2016 as the last year of existence
The possible values of amount raised for
Year 2014 = 2 or 3, Year 2015 = 3 or 2 and Year 2016 = 1
The possible sum = Rs 7 crores (maximum)
So, the last year of existence for the firm Czechy has to be 2017 with only possible values
Year 2013 = 1, Year 2014 = 2, Year 2015 = 3, Year 2016 = 2 and Year 2017 = 1
Thus, the total amount raised = Rs 9 crores
Now for Drjbna,
First year of existence, 2011 = Rs 1 crore = Last year of existence, 2015
Total amount raised = Rs 10 crores
The only possible value of amount raised for
Year 2012 = 2, Year 2013 = 4 and Year 2014 = 2
Now for Elavalaki,
Total amount raised = Rs 13 crores
First year of existence, 2011 = Rs 1 crore but last year of existence is not given
Considering the minimum amounts the possible values of amount raised for
Year 2010 = 1, Year 2011 = 2, Year 2012 = 3 or 4, Year 2013 = 4 or 3, Year 2014 = 2 and Year 2015 = 1 (such that Year 2015 is the last year of existence)
Considering the maximum amounts the possible values of amount raised for
Year 2010 = 1, Year 2011 = 3, Year 2012 = 5, Year 2013 = 3, Year 2014 = 1 (such that Year 2014 is the last year of existence)
The rest of the information can be gathered as follows-
The total amount of money raised in 2015 can be either Rs. 7 crores or Rs. 8 crores
3. What is the largest possible total amount of money (in Rs. crores) that could have been raised in 2013?
Given that each firm raised Rs 1 crore in its first and last year. Also, each annual increase and decrease was either of Rs 1 crore or by Rs 2 crores.
Let us consider for Alfloo,
First year of existence, 2009 = Rs 1 crore = Last year of existence, 2016
Let amount raised in 2010, 2011, 2012, 2013, 2014, 2015 be a, b, c, d, e and f respectively
Solving, 1 + a + b + c + d + e + f + 1 = 21
⇒ a + b + c + d + e + f = 19
Now, even if we consider minimum annual increase and decrease annually,
The values can be a = 2, b = 3, c = 4 or 5, d = 5 or 4, e = 3 and f = 2
Now for Bzygoo,
First year of existence, 2012 = Rs 1 crore = Last year of existence, 2015
The possibilities for the amount raised in 2013 = 2 or 3 and in 2014 = 3 or 2 respectively
Thus the total amount raised by Bzygoo = Rs 7 crores
Now for Czechy,
First year of existence, 2013 = Rs 1 crore
Total amount raised = Rs 9 crores
Now, if we consider Year 2016 as the last year of existence
The possible values of amount raised for
Year 2014 = 2 or 3, Year 2015 = 3 or 2 and Year 2016 = 1
The possible sum = Rs 7 crores (maximum)
So, the last year of existence for the firm Czechy has to be 2017 with only possible values
Year 2013 = 1, Year 2014 = 2, Year 2015 = 3, Year 2016 = 2 and Year 2017 = 1
Thus, the total amount raised = Rs 9 crores
Now for Drjbna,
First year of existence, 2011 = Rs 1 crore = Last year of existence, 2015
Total amount raised = Rs 10 crores
The only possible value of amount raised for
Year 2012 = 2, Year 2013 = 4 and Year 2014 = 2
Now for Elavalaki,
Total amount raised = Rs 13 crores
First year of existence, 2011 = Rs 1 crore but last year of existence is not given
Considering the minimum amounts the possible values of amount raised for
Year 2010 = 1, Year 2011 = 2, Year 2012 = 3 or 4, Year 2013 = 4 or 3, Year 2014 = 2 and Year 2015 = 1 (such that Year 2015 is the last year of existence)
Considering the maximum amounts the possible values of amount raised for
Year 2010 = 1, Year 2011 = 3, Year 2012 = 5, Year 2013 = 3, Year 2014 = 1 (such that Year 2014 is the last year of existence)
The rest of the information can be gathered as follows-
The largest possible total amount of money that could have been raised in 2013 = Rs. 17 crores
4. If Elavalaki raised Rs. 3 crores in 2013, then what is the smallest possible total amount of money (in Rs. crores) that could have been raised by all the companies in 2012?
- 11
- 9
- 12
- 10
Given that each firm raised Rs 1 crore in its first and last year. Also, each annual increase and decrease was either of Rs 1 crore or by Rs 2 crores.
Let us consider for Alfloo,
First year of existence, 2009 = Rs 1 crore = Last year of existence, 2016
Let amount raised in 2010, 2011, 2012, 2013, 2014, 2015 be a, b, c, d, e and f respectively
Solving, 1 + a + b + c + d + e + f + 1 = 21
⇒ a + b + c + d + e + f = 19
Now, even if we consider minimum annual increase and decrease annually,
The values can be a = 2, b = 3, c = 4 or 5, d = 5 or 4, e = 3 and f = 2
Now for Bzygoo,
First year of existence, 2012 = Rs 1 crore = Last year of existence, 2015
The possibilities for the amount raised in 2013 = 2 or 3 and in 2014 = 3 or 2 respectively
Thus the total amount raised by Bzygoo = Rs 7 crores
Now for Czechy,
First year of existence, 2013 = Rs 1 crore
Total amount raised = Rs 9 crores
Now, if we consider Year 2016 as the last year of existence
The possible values of amount raised for
Year 2014 = 2 or 3, Year 2015 = 3 or 2 and Year 2016 = 1
The possible sum = Rs 7 crores (maximum)
So, the last year of existence for the firm Czechy has to be 2017 with only possible values
Year 2013 = 1, Year 2014 = 2, Year 2015 = 3, Year 2016 = 2 and Year 2017 = 1
Thus, the total amount raised = Rs 9 crores
Now for Drjbna,
First year of existence, 2011 = Rs 1 crore = Last year of existence, 2015
Total amount raised = Rs 10 crores
The only possible value of amount raised for
Year 2012 = 2, Year 2013 = 4 and Year 2014 = 2
Now for Elavalaki,
Total amount raised = Rs 13 crores
First year of existence, 2011 = Rs 1 crore but last year of existence is not given
Considering the minimum amounts the possible values of amount raised for
Year 2010 = 1, Year 2011 = 2, Year 2012 = 3 or 4, Year 2013 = 4 or 3, Year 2014 = 2 and Year 2015 = 1 (such that Year 2015 is the last year of existence)
Considering the maximum amounts the possible values of amount raised for
Year 2010 = 1, Year 2011 = 3, Year 2012 = 5, Year 2013 = 3, Year 2014 = 1 (such that Year 2014 is the last year of existence)
The rest of the information can be gathered as follows-
If Elavalaki raised Rs. 3 crores in 2013, then Elavalaki raised Rs. 4 crores in 2014
Hence, the smallest possible total amount of money raised in 2012
= 4 + 1 + 2 + 4 = Rs. 11 crores
5. If the total amount of money raised in 2014 is Rs. 12 crores, then which of the following is not possible?
- Alfloo raised the same amount of money as Bzygoo in 2014.
- Bzygoo raised more money than Elavalaki in 2014.
- Alfloo raised the same amount of money as Drjbna in 2013.
- Bzygoo raised the same amount of money as Elavalaki in 2013.
Given that each firm raised Rs 1 crore in its first and last year. Also, each annual increase and decrease was either of Rs 1 crore or by Rs 2 crores.
Let us consider for Alfloo,
First year of existence, 2009 = Rs 1 crore = Last year of existence, 2016
Let amount raised in 2010, 2011, 2012, 2013, 2014, 2015 be a, b, c, d, e and f respectively
Solving, 1 + a + b + c + d + e + f + 1 = 21
⇒ a + b + c + d + e + f = 19
Now, even if we consider minimum annual increase and decrease annually,
The values can be a = 2, b = 3, c = 4 or 5, d = 5 or 4, e = 3 and f = 2
Now for Bzygoo,
First year of existence, 2012 = Rs 1 crore = Last year of existence, 2015
The possibilities for the amount raised in 2013 = 2 or 3 and in 2014 = 3 or 2 respectively
Thus the total amount raised by Bzygoo = Rs 7 crores
Now for Czechy,
First year of existence, 2013 = Rs 1 crore
Total amount raised = Rs 9 crores
Now, if we consider Year 2016 as the last year of existence
The possible values of amount raised for
Year 2014 = 2 or 3, Year 2015 = 3 or 2 and Year 2016 = 1
The possible sum = Rs 7 crores (maximum)
So, the last year of existence for the firm Czechy has to be 2017 with only possible values
Year 2013 = 1, Year 2014 = 2, Year 2015 = 3, Year 2016 = 2 and Year 2017 = 1
Thus, the total amount raised = Rs 9 crores
Now for Drjbna,
First year of existence, 2011 = Rs 1 crore = Last year of existence, 2015
Total amount raised = Rs 10 crores
The only possible value of amount raised for
Year 2012 = 2, Year 2013 = 4 and Year 2014 = 2
Now for Elavalaki,
Total amount raised = Rs 13 crores
First year of existence, 2011 = Rs 1 crore but last year of existence is not given
Considering the minimum amounts the possible values of amount raised for
Year 2010 = 1, Year 2011 = 2, Year 2012 = 3 or 4, Year 2013 = 4 or 3, Year 2014 = 2 and Year 2015 = 1 (such that Year 2015 is the last year of existence)
Considering the maximum amounts the possible values of amount raised for
Year 2010 = 1, Year 2011 = 3, Year 2012 = 5, Year 2013 = 3, Year 2014 = 1 (such that Year 2014 is the last year of existence)
The rest of the information can be gathered as follows-
If total amount raised in 2014 = Rs. 12 crores
⇒ amount raised by Bzygoo in 2014 = Rs. 3 crores
⇒ amount raised by Bzygoo in 2013 = Rs 2 crores
Also, amount raised by Elavalaki in 2013 = Rs 3 crore or Rs 4 crores
Hence, Bzygoo raised the same amount of money as Elavalaki in 2013, it is not possible
CAT 2023 | DILR Set 2
Three participants – Akhil, Bimal and Chatur participate in a random draw competition for five days. Every day, each participant randomly picks up a ball numbered between 1 and 9. The number on the ball determines his score on that day. The total score of a participant is the sum of his scores attained in the five days. The total score of a day is the sum of participants’ scores on that day. The 2-day average on a day, except on Day 1, is the average of the total scores of that day and of the previous day. For example, if the total scores of Day 1 and Day 2 are 25 and 20, then the 2-day average on Day 2 is calculated as 22.5. Table 1 gives the 2-day averages for Days 2 through 5.
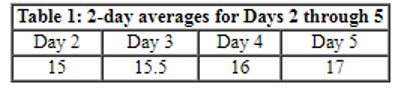
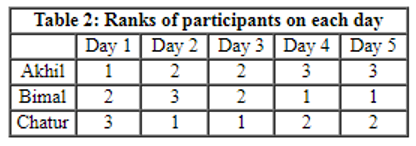
Participants are ranked each day, with the person having the maximum score being awarded the minimum rank (1) on that day. If there is a tie, all participants with the tied score are awarded the best available rank. For example, if on a day Akhil, Bimal, and Chatur score 8, 7 and 7 respectively, then their ranks will be 1, 2 and 2 respectively on that day. These ranks are given in Table 2.
The following information is also known.
- Chatur always scores in multiples of 3. His score on Day 2 is the unique highest score in the competition. His minimum score is observed only on Day 1, and it matches Akhil’s score on Day 4.
- The total score on Day 3 is the same as the total score on Day 4.
- Bimal’s scores are the same on Day 1 and Day 3.
6. What is Akhil's score on Day 1?
- 7
- 5
- 6
- 8
Let the total score of Day 1, Day 2, Day 3, Day 4 and Day 5 of all the participants be a, b, c, d and e respectively.
As per the Table 1,
a + b = 15 × 2 = 30, b + c = 15.5 × 2 = 31, c + d = 16 × 2 = 32 and d + e = 17 × 2 = 34
Point 2, total score on Day 3 = total score on Day 4
⇒ c = d = 16 (each)
⇒ e = 34 – 16 = 18, b = 31 – 16 = 15 and a = 30 – 15 = 15
Point 1, Chatur score on any day = 3, 6 or 9
The only possibility of his Day 2 score being unique highest = 9
His only minimum score on Day 1 = 3
⇒ Chatur’s score on Day 3, Day 4 and Day 5 = 6 (each)
Also, Akhil’s Day 4 score = Chatur’s Day 1 score = 3
⇒ Bimal’s Day 4 score = 16 – (3 + 6) = 7
Now being same rank,
Akhil’s Day 3 score = Bimal’s Day 3 score = 5 (each)
Point 3, Bimal’s Day 1 score = Bimal’s Day 3 score = 5
⇒ Akhil’s Day 1 score = 15 – (5 + 3) = 7
Now for Day 2, let the score of Akhil = p and Bimal = q
Solving, p + q + 9 = 15 ⇒ p + q = 6
Since, the rank of Akhil is 2 and Bimal is 3
Possible values of p = 4 or 5 and q = 2 or 1
Now for Day 5, let the score of Akhil = x and Bimal = y
Solving, x + y + 6 = 18 ⇒ x + y = 12
Since, the rank of Akhil is 3 and Bimal is 1
Possible value of x = 5 or 4 and y = 7 or 8
(y cannot be 9 as that being unique highest)
The rest of the information can be gathered as follows-
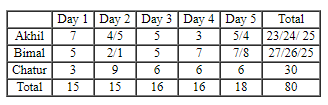Akhil’s score on Day 1 = 7
7. Who attains the maximum total score?
- Akhil
- Cannot be determined
- Bimal
- Chatur
Let the total score of Day 1, Day 2, Day 3, Day 4 and Day 5 of all the participants be a, b, c, d and e respectively.
As per the Table 1,
a + b = 15 × 2 = 30, b + c = 15.5 × 2 = 31, c + d = 16 × 2 = 32 and d + e = 17 × 2 = 34
Point 2, total score on Day 3 = total score on Day 4
⇒ c = d = 16 (each)
⇒ e = 34 – 16 = 18, b = 31 – 16 = 15 and a = 30 – 15 = 15
Point 1, Chatur score on any day = 3, 6 or 9
The only possibility of his Day 2 score being unique highest = 9
His only minimum score on Day 1 = 3
⇒ Chatur’s score on Day 3, Day 4 and Day 5 = 6 (each)
Also, Akhil’s Day 4 score = Chatur’s Day 1 score = 3
⇒ Bimal’s Day 4 score = 16 – (3 + 6) = 7
Now being same rank,
Akhil’s Day 3 score = Bimal’s Day 3 score = 5 (each)
Point 3, Bimal’s Day 1 score = Bimal’s Day 3 score = 5
⇒ Akhil’s Day 1 score = 15 – (5 + 3) = 7
Now for Day 2, let the score of Akhil = p and Bimal = q
Solving, p + q + 9 = 15 ⇒ p + q = 6
Since, the rank of Akhil is 2 and Bimal is 3
Possible values of p = 4 or 5 and q = 2 or 1
Now for Day 5, let the score of Akhil = x and Bimal = y
Solving, x + y + 6 = 18 ⇒ x + y = 12
Since, the rank of Akhil is 3 and Bimal is 1
Possible value of x = 5 or 4 and y = 7 or 8
(y cannot be 9 as that being unique highest)
The rest of the information can be gathered as follows-
Chatur attains the maximum possible score
8. What is the minimum possible total score of Bimal? (type in numerical)
Let the total score of Day 1, Day 2, Day 3, Day 4 and Day 5 of all the participants be a, b, c, d and e respectively.
As per the Table 1,
a + b = 15 × 2 = 30, b + c = 15.5 × 2 = 31, c + d = 16 × 2 = 32 and d + e = 17 × 2 = 34
Point 2, total score on Day 3 = total score on Day 4
⇒ c = d = 16 (each)
⇒ e = 34 – 16 = 18, b = 31 – 16 = 15 and a = 30 – 15 = 15
Point 1, Chatur score on any day = 3, 6 or 9
The only possibility of his Day 2 score being unique highest = 9
His only minimum score on Day 1 = 3
⇒ Chatur’s score on Day 3, Day 4 and Day 5 = 6 (each)
Also, Akhil’s Day 4 score = Chatur’s Day 1 score = 3
⇒ Bimal’s Day 4 score = 16 – (3 + 6) = 7
Now being same rank,
Akhil’s Day 3 score = Bimal’s Day 3 score = 5 (each)
Point 3, Bimal’s Day 1 score = Bimal’s Day 3 score = 5
⇒ Akhil’s Day 1 score = 15 – (5 + 3) = 7
Now for Day 2, let the score of Akhil = p and Bimal = q
Solving, p + q + 9 = 15 ⇒ p + q = 6
Since, the rank of Akhil is 2 and Bimal is 3
Possible values of p = 4 or 5 and q = 2 or 1
Now for Day 5, let the score of Akhil = x and Bimal = y
Solving, x + y + 6 = 18 ⇒ x + y = 12
Since, the rank of Akhil is 3 and Bimal is 1
Possible value of x = 5 or 4 and y = 7 or 8
(y cannot be 9 as that being unique highest)
The rest of the information can be gathered as follows-
The minimum possible total score of Bimal = 25
9. If the total score of Bimal is a multiple of 3, what is the score of Akhil on Day 2?
- 5
- 4
- Cannot be determined
- 6
Let the total score of Day 1, Day 2, Day 3, Day 4 and Day 5 of all the participants be a, b, c, d and e respectively.
As per the Table 1,
a + b = 15 × 2 = 30, b + c = 15.5 × 2 = 31, c + d = 16 × 2 = 32 and d + e = 17 × 2 = 34
Point 2, total score on Day 3 = total score on Day 4
⇒ c = d = 16 (each)
⇒ e = 34 – 16 = 18, b = 31 – 16 = 15 and a = 30 – 15 = 15
Point 1, Chatur score on any day = 3, 6 or 9
The only possibility of his Day 2 score being unique highest = 9
His only minimum score on Day 1 = 3
⇒ Chatur’s score on Day 3, Day 4 and Day 5 = 6 (each)
Also, Akhil’s Day 4 score = Chatur’s Day 1 score = 3
⇒ Bimal’s Day 4 score = 16 – (3 + 6) = 7
Now being same rank,
Akhil’s Day 3 score = Bimal’s Day 3 score = 5 (each)
Point 3, Bimal’s Day 1 score = Bimal’s Day 3 score = 5
⇒ Akhil’s Day 1 score = 15 – (5 + 3) = 7
Now for Day 2, let the score of Akhil = p and Bimal = q
Solving, p + q + 9 = 15 ⇒ p + q = 6
Since, the rank of Akhil is 2 and Bimal is 3
Possible values of p = 4 or 5 and q = 2 or 1
Now for Day 5, let the score of Akhil = x and Bimal = y
Solving, x + y + 6 = 18 ⇒ x + y = 12
Since, the rank of Akhil is 3 and Bimal is 1
Possible value of x = 5 or 4 and y = 7 or 8
(y cannot be 9 as that being unique highest)
The rest of the information can be gathered as follows-
If the total score of Bimal is a multiple of 3, the only possibility = 27
⇒ Bimal’s Day 2 score = 2 ⇒ Akhil’s Day 2 score = 4
10. If Akhil attains a total score of 24, then what is the total score of Bimal? (type in numerical)
Let the total score of Day 1, Day 2, Day 3, Day 4 and Day 5 of all the participants be a, b, c, d and e respectively.
As per the Table 1,
a + b = 15 × 2 = 30, b + c = 15.5 × 2 = 31, c + d = 16 × 2 = 32 and d + e = 17 × 2 = 34
Point 2, total score on Day 3 = total score on Day 4
⇒ c = d = 16 (each)
⇒ e = 34 – 16 = 18, b = 31 – 16 = 15 and a = 30 – 15 = 15
Point 1, Chatur score on any day = 3, 6 or 9
The only possibility of his Day 2 score being unique highest = 9
His only minimum score on Day 1 = 3
⇒ Chatur’s score on Day 3, Day 4 and Day 5 = 6 (each)
Also, Akhil’s Day 4 score = Chatur’s Day 1 score = 3
⇒ Bimal’s Day 4 score = 16 – (3 + 6) = 7
Now being same rank,
Akhil’s Day 3 score = Bimal’s Day 3 score = 5 (each)
Point 3, Bimal’s Day 1 score = Bimal’s Day 3 score = 5
⇒ Akhil’s Day 1 score = 15 – (5 + 3) = 7
Now for Day 2, let the score of Akhil = p and Bimal = q
Solving, p + q + 9 = 15 ⇒ p + q = 6
Since, the rank of Akhil is 2 and Bimal is 3
Possible values of p = 4 or 5 and q = 2 or 1
Now for Day 5, let the score of Akhil = x and Bimal = y
Solving, x + y + 6 = 18 ⇒ x + y = 12
Since, the rank of Akhil is 3 and Bimal is 1
Possible value of x = 5 or 4 and y = 7 or 8
(y cannot be 9 as that being unique highest)
The rest of the information can be gathered as follows-
If Akhil’s total score = 24 ⇒ Bimal’s total score = 26. Answer is 26
CAT 2023 | DILR Set 3
There are nine boxes arranged in a 3×3 array as shown in Tables 1 and 2. Each box contains three sacks. Each sack has a certain number of coins, between 1 and 9, both inclusive.
The average number of coins per sack in the boxes are all distinct integers. The total number of coins in each row is the same. The total number of coins in each column is also the same.
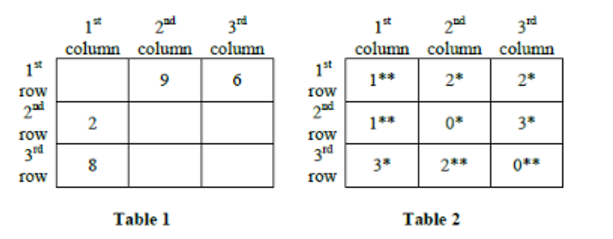
Table 1 gives information regarding the median of the numbers of coins in the three sacks in a box for some of the boxes. In Table 2 each box has a number which represents the number of sacks in that box having more than 5 coins. That number is followed by a * if the sacks in that box satisfy exactly one among the following three conditions, and it is followed by ** if two or more of these conditions are satisfied.
- The minimum among the numbers of coins in the three sacks in the box is 1.
- The median of the numbers of coins in the three sacks is 1.
- The maximum among the numbers of coins in the three sacks in the box is 9.
11. What is the total number of coins in all the boxes in the 3rd row?
- 15
- 45
- 36
- 30
Firstly, if all the given three conditions satisfy, the sum of number of coins in the box could be = 1 + 1 + 9 = 11, but that is not giving the average as distinct integer. Thus, either exactly one condition satisfies or exactly two conditions satisfy.
For 1st row, 2nd column box, the median number of coins is 9, so the maximum number of coins is also 9. Thus as mentioned in Table 2, two sacks have more than 5 coins and exactly one condition (iii) satisfies. So, the third sack must contain coins less than or equal to 5. Also, the average number of coins per sack in any box is a distinct integer, so the only value that satisfies the coins in third sack = 3, such that the average coins in the box = (3 + 9 + 9)/3 = 7
For 2nd row, 1st column box, given that two or more conditions satisfies, but since the median number of coins = 2, so, exactly two conditions (i and iii) satisfies. Also, only one sack contains more than 5 coins. Thus the average coins in the box = 1 + 2 + 9 = 12/3 = 4
For 3rd row, 1st column, median number of coins in the box = 8, all three sacks contains more than 5 coins and only 1 condition satisfies. So, that condition must be (iii) condition i.e. the maximum coins = 9. Also, to make average an integer, the number of coins in third sack must be 7. The average number of coins in the box = (7 + 8 + 9)/3 = 8
For 3rd row, 2nd column, two conditions satisfies and two sacks contain more than 5 coins. Thus, the conditions that satisfy must be (i) and (iii). So, the only possible average in the box = (1 + 8 + 9)/3 = 6
Now, since for each and each column the total is same, so the average is also the same. Sum of distinct integers from 1 to 9 = 45, so the sum of each row and each column = 15, which is also the average of the boxes for each row and each column. Hence, the sum of number of coins in each row and each column must be = 45
The sum for 1st row, 1st column = 45 – (12 + 36) = 9
Only possible average = (1 + 1 + 7)/3 = 3 satisfying other given conditions as well
The sum of 2nd row, 2nd column = 45 – (21 + 18) = 6
Only possible average = (1 + 2 + 3)/3 = 2 satisfying other given conditions as well
The sum of 1st row, 3rd column = 45 – (9 + 21) = 15
Only possible average = (1 + 6 + 8)/3 = 5 satisfying other given conditions as well
The sum of 2nd row, 3rd column = 45 – (12 + 6) = 27
Only possible average = (9 + 9 + 9)/3 = 9 satisfying other given conditions as well
The sum of 3rd row, 3rd column = 45 – (24 + 18) = 3
Only possible average = (1 + 1 + 1)/3 = 1 satisfying other given conditions as well
The rest of the information can be gathered as follows-
The total number of coins in all the boxes in the 3rd row = 45
12. How many boxes have at least one sack containing 9 coins?
- 3
- 8
- 4
- 5
Firstly, if all the given three conditions satisfy, the sum of number of coins in the box could be = 1 + 1 + 9 = 11, but that is not giving the average as distinct integer. Thus, either exactly one condition satisfies or exactly two conditions satisfy.
For 1st row, 2nd column box, the median number of coins is 9, so the maximum number of coins is also 9. Thus as mentioned in Table 2, two sacks have more than 5 coins and exactly one condition (iii) satisfies. So, the third sack must contain coins less than or equal to 5. Also, the average number of coins per sack in any box is a distinct integer, so the only value that satisfies the coins in third sack = 3, such that the average coins in the box = (3 + 9 + 9)/3 = 7
For 2nd row, 1st column box, given that two or more conditions satisfies, but since the median number of coins = 2, so, exactly two conditions (i and iii) satisfies. Also, only one sack contains more than 5 coins. Thus the average coins in the box = 1 + 2 + 9 = 12/3 = 4
For 3rd row, 1st column, median number of coins in the box = 8, all three sacks contains more than 5 coins and only 1 condition satisfies. So, that condition must be (iii) condition i.e. the maximum coins = 9. Also, to make average an integer, the number of coins in third sack must be 7. The average number of coins in the box = (7 + 8 + 9)/3 = 8
For 3rd row, 2nd column, two conditions satisfies and two sacks contain more than 5 coins. Thus, the conditions that satisfy must be (i) and (iii). So, the only possible average in the box = (1 + 8 + 9)/3 = 6
Now, since for each and each column the total is same, so the average is also the same. Sum of distinct integers from 1 to 9 = 45, so the sum of each row and each column = 15, which is also the average of the boxes for each row and each column. Hence, the sum of number of coins in each row and each column must be = 45
The sum for 1st row, 1st column = 45 – (12 + 36) = 9
Only possible average = (1 + 1 + 7)/3 = 3 satisfying other given conditions as well
The sum of 2nd row, 2nd column = 45 – (21 + 18) = 6
Only possible average = (1 + 2 + 3)/3 = 2 satisfying other given conditions as well
The sum of 1st row, 3rd column = 45 – (9 + 21) = 15
Only possible average = (1 + 6 + 8)/3 = 5 satisfying other given conditions as well
The sum of 2nd row, 3rd column = 45 – (12 + 6) = 27
Only possible average = (9 + 9 + 9)/3 = 9 satisfying other given conditions as well
The sum of 3rd row, 3rd column = 45 – (24 + 18) = 3
Only possible average = (1 + 1 + 1)/3 = 1 satisfying other given conditions as well
The rest of the information can be gathered as follows-
The boxes having at least one sack containing 9 coins = 5
(1st row, 2nd column), (2nd row, 1st column), (2nd row, 3rd column), (3rd row, 1st column) and (3rd row, 2nd column)
13. For how many boxes are the average and median of the numbers of coins contained in the three sacks in that box the same?
Firstly, if all the given three conditions satisfy, the sum of number of coins in the box could be = 1 + 1 + 9 = 11, but that is not giving the average as distinct integer. Thus, either exactly one condition satisfies or exactly two conditions satisfy.
For 1st row, 2nd column box, the median number of coins is 9, so the maximum number of coins is also 9. Thus as mentioned in Table 2, two sacks have more than 5 coins and exactly one condition (iii) satisfies. So, the third sack must contain coins less than or equal to 5. Also, the average number of coins per sack in any box is a distinct integer, so the only value that satisfies the coins in third sack = 3, such that the average coins in the box = (3 + 9 + 9)/3 = 7
For 2nd row, 1st column box, given that two or more conditions satisfies, but since the median number of coins = 2, so, exactly two conditions (i and iii) satisfies. Also, only one sack contains more than 5 coins. Thus the average coins in the box = 1 + 2 + 9 = 12/3 = 4
For 3rd row, 1st column, median number of coins in the box = 8, all three sacks contains more than 5 coins and only 1 condition satisfies. So, that condition must be (iii) condition i.e. the maximum coins = 9. Also, to make average an integer, the number of coins in third sack must be 7. The average number of coins in the box = (7 + 8 + 9)/3 = 8
For 3rd row, 2nd column, two conditions satisfies and two sacks contain more than 5 coins. Thus, the conditions that satisfy must be (i) and (iii). So, the only possible average in the box = (1 + 8 + 9)/3 = 6
Now, since for each and each column the total is same, so the average is also the same. Sum of distinct integers from 1 to 9 = 45, so the sum of each row and each column = 15, which is also the average of the boxes for each row and each column. Hence, the sum of number of coins in each row and each column must be = 45
The sum for 1st row, 1st column = 45 – (12 + 36) = 9
Only possible average = (1 + 1 + 7)/3 = 3 satisfying other given conditions as well
The sum of 2nd row, 2nd column = 45 – (21 + 18) = 6
Only possible average = (1 + 2 + 3)/3 = 2 satisfying other given conditions as well
The sum of 1st row, 3rd column = 45 – (9 + 21) = 15
Only possible average = (1 + 6 + 8)/3 = 5 satisfying other given conditions as well
The sum of 2nd row, 3rd column = 45 – (12 + 6) = 27
Only possible average = (9 + 9 + 9)/3 = 9 satisfying other given conditions as well
The sum of 3rd row, 3rd column = 45 – (24 + 18) = 3
Only possible average = (1 + 1 + 1)/3 = 1 satisfying other given conditions as well
The rest of the information can be gathered as follows-
14. How many sacks have exactly one coin?
Firstly, if all the given three conditions satisfy, the sum of number of coins in the box could be = 1 + 1 + 9 = 11, but that is not giving the average as distinct integer. Thus, either exactly one condition satisfies or exactly two conditions satisfy.
For 1st row, 2nd column box, the median number of coins is 9, so the maximum number of coins is also 9. Thus as mentioned in Table 2, two sacks have more than 5 coins and exactly one condition (iii) satisfies. So, the third sack must contain coins less than or equal to 5. Also, the average number of coins per sack in any box is a distinct integer, so the only value that satisfies the coins in third sack = 3, such that the average coins in the box = (3 + 9 + 9)/3 = 7
For 2nd row, 1st column box, given that two or more conditions satisfies, but since the median number of coins = 2, so, exactly two conditions (i and iii) satisfies. Also, only one sack contains more than 5 coins. Thus the average coins in the box = 1 + 2 + 9 = 12/3 = 4
For 3rd row, 1st column, median number of coins in the box = 8, all three sacks contains more than 5 coins and only 1 condition satisfies. So, that condition must be (iii) condition i.e. the maximum coins = 9. Also, to make average an integer, the number of coins in third sack must be 7. The average number of coins in the box = (7 + 8 + 9)/3 = 8
For 3rd row, 2nd column, two conditions satisfies and two sacks contain more than 5 coins. Thus, the conditions that satisfy must be (i) and (iii). So, the only possible average in the box = (1 + 8 + 9)/3 = 6
Now, since for each and each column the total is same, so the average is also the same. Sum of distinct integers from 1 to 9 = 45, so the sum of each row and each column = 15, which is also the average of the boxes for each row and each column. Hence, the sum of number of coins in each row and each column must be = 45
The sum for 1st row, 1st column = 45 – (12 + 36) = 9
Only possible average = (1 + 1 + 7)/3 = 3 satisfying other given conditions as well
The sum of 2nd row, 2nd column = 45 – (21 + 18) = 6
Only possible average = (1 + 2 + 3)/3 = 2 satisfying other given conditions as well
The sum of 1st row, 3rd column = 45 – (9 + 21) = 15
Only possible average = (1 + 6 + 8)/3 = 5 satisfying other given conditions as well
The sum of 2nd row, 3rd column = 45 – (12 + 6) = 27
Only possible average = (9 + 9 + 9)/3 = 9 satisfying other given conditions as well
The sum of 3rd row, 3rd column = 45 – (24 + 18) = 3
Only possible average = (1 + 1 + 1)/3 = 1 satisfying other given conditions as well
The rest of the information can be gathered as follows-
Number of sacks having exactly one coin = 9
15. In how many boxes do all three sacks contain different numbers of coins?
Firstly, if all the given three conditions satisfy, the sum of number of coins in the box could be = 1 + 1 + 9 = 11, but that is not giving the average as distinct integer. Thus, either exactly one condition satisfies or exactly two conditions satisfy.
For 1st row, 2nd column box, the median number of coins is 9, so the maximum number of coins is also 9. Thus as mentioned in Table 2, two sacks have more than 5 coins and exactly one condition (iii) satisfies. So, the third sack must contain coins less than or equal to 5. Also, the average number of coins per sack in any box is a distinct integer, so the only value that satisfies the coins in third sack = 3, such that the average coins in the box = (3 + 9 + 9)/3 = 7
For 2nd row, 1st column box, given that two or more conditions satisfies, but since the median number of coins = 2, so, exactly two conditions (i and iii) satisfies. Also, only one sack contains more than 5 coins. Thus the average coins in the box = 1 + 2 + 9 = 12/3 = 4
For 3rd row, 1st column, median number of coins in the box = 8, all three sacks contains more than 5 coins and only 1 condition satisfies. So, that condition must be (iii) condition i.e. the maximum coins = 9. Also, to make average an integer, the number of coins in third sack must be 7. The average number of coins in the box = (7 + 8 + 9)/3 = 8
For 3rd row, 2nd column, two conditions satisfies and two sacks contain more than 5 coins. Thus, the conditions that satisfy must be (i) and (iii). So, the only possible average in the box = (1 + 8 + 9)/3 = 6
Now, since for each and each column the total is same, so the average is also the same. Sum of distinct integers from 1 to 9 = 45, so the sum of each row and each column = 15, which is also the average of the boxes for each row and each column. Hence, the sum of number of coins in each row and each column must be = 45
The sum for 1st row, 1st column = 45 – (12 + 36) = 9
Only possible average = (1 + 1 + 7)/3 = 3 satisfying other given conditions as well
The sum of 2nd row, 2nd column = 45 – (21 + 18) = 6
Only possible average = (1 + 2 + 3)/3 = 2 satisfying other given conditions as well
The sum of 1st row, 3rd column = 45 – (9 + 21) = 15
Only possible average = (1 + 6 + 8)/3 = 5 satisfying other given conditions as well
The sum of 2nd row, 3rd column = 45 – (12 + 6) = 27
Only possible average = (9 + 9 + 9)/3 = 9 satisfying other given conditions as well
The sum of 3rd row, 3rd column = 45 – (24 + 18) = 3
Only possible average = (1 + 1 + 1)/3 = 1 satisfying other given conditions as well
The rest of the information can be gathered as follows-
Number of boxes having all three sacks contain different number of coins = 5
(1st row, 3rd column), (2nd row, 1st column), (2nd row, 2nd column), (3rd row, 1st column) and (3rd row, 2nd column)
CAT 2023 | DILR Set 4
Anjali, Bipasha, and Chitra visited an entertainment park that has four rides. Each ride lasts one hour and can accommodate one visitor at one point. All rides begin at 9 am and must be completed by 5 pm except for Ride-3, for which the last ride has to be completed by 1 pm.
Ride gates open every 30 minutes, e.g. 10 am, 10:30 am, and so on. Whenever a ride gate opens, and there is no visitor inside, the first visitor waiting in the queue buys the ticket just before taking the ride. The ticket prices are Rs. 20, Rs. 50, Rs. 30 and Rs. 40 for Rides 1 to 4, respectively. Each of the three visitors took at least one ride and did not necessarily take all rides. None of them took the same ride more than once. The movement time from one ride to another is negligible, and a visitor leaves the ride immediately after the completion of the ride. No one takes a break inside the park unless mentioned explicitly.
The following information is also known.
- Chitra never waited in the queue and completed her visit by 11 am after spending Rs. 50 to pay for the ticket(s).
- Anjali took Ride-1 at 11 am after waiting for 30 mins for Chitra to complete it. It was the only ride where Anjali waited.
- Bipasha began her first of three rides at 11:30 am. All three visitors incurred the same amount of ticket expense by 12:15 pm.
- The last ride taken by Anjali and Bipasha was the same, where Bipasha waited 30 mins for Anjali to complete her ride. Before standing in the queue for that ride, Bipasha took a 1-hour coffee break after completing her previous ride.
16. What was the total amount spent on tickets (in Rs.) by Bipasha?
- 100
- 120
- 110
- 90
Since the time slot varies for different visitors as well as rides, so let’s arrange the data with respect to rides vs visitors and fill the time slot and corresponding spending accordingly.
From point 1, Chitra spend Rs 50 and completed her rides by 11 am without any wait, so she must have taken 2 rides Ride-1 (Rs 20) and Ride-3 (Rs 30)
From point 2, Anjali took Ride-1 at 11 am after waiting for Chitra to complete, so Chitra took Ride-3 from 9 am to 10 am and Ride-1 from 10 am to 11 am respectively
From point 3, Bipasha first of three rides is from 11:30 am to 12:30 pm
Also, by 12:15 pm, all three have spent same amount = Rs 50 each (same as Chitra’s complete spending by 11 am)
So, Bipasha’s ride from 11:30 am to 12:30 am must be Ride 2 amounting Rs 50
Also, Anjali’s second ride must be Ride-3 from 12 pm to 1 pm (without any wait and total spending of Rs 50 by 12:15 pm)
Also, Bipasha’s other two rides cannot be Ride-3 as it should be completed by 1 pm
From point 4, the last ride taken by Anjali and Bipasha was the same
Let’s say Anjali’s last ride was Ride-4 from 1 pm to 2 pm just after Ride-3 taken from 12 pm to 1 pm as Anjali never took a break mentioned
So, for Bipasha’s last ride, she could have reached 1:30 pm and taken the Ride-4 from 2 pm to 3 pm after 30 mins wait for Anjali
So, Bipasha’s second ride could be Ride-1 from 12:30 pm to 1:30 pm
But that is not possible as she took a 1-hour coffee break after completing her second ride.
Thus, this is only possible if Anjali took Ride-2 from 1 pm to 2 pm and her last ride is Ride-4 from 2 pm to 3 pm respectively
Such that Bipasha’s second ride is Ride-1 from 12:30 pm to 1:30 pm and then 1-hour coffee break from 1:30 pm to 2:30 pm and then 30 min wait for Anjali from 2:30 pm to 3 pm and finally the last ride, Ride-4 from 3 pm to 4 pm
The rest of the information can be gathered as follows-
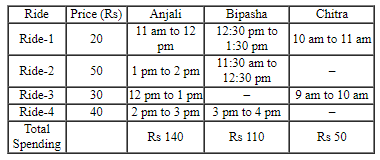The total amount spent on tickets by Bipasha = Rs 110
17. Which were all the rides that Anjali completed by 2:00 pm?
- Ride-1 and Ride-4
- Ride-1, Ride-2, and Ride-4
- Ride-1, Ride-2, and Ride-3
- Ride-1 and Ride-3
Since the time slot varies for different visitors as well as rides, so let’s arrange the data with respect to rides vs visitors and fill the time slot and corresponding spending accordingly.
From point 1, Chitra spend Rs 50 and completed her rides by 11 am without any wait, so she must have taken 2 rides Ride-1 (Rs 20) and Ride-3 (Rs 30)
From point 2, Anjali took Ride-1 at 11 am after waiting for Chitra to complete, so Chitra took Ride-3 from 9 am to 10 am and Ride-1 from 10 am to 11 am respectively
From point 3, Bipasha first of three rides is from 11:30 am to 12:30 pm
Also, by 12:15 pm, all three have spent same amount = Rs 50 each (same as Chitra’s complete spending by 11 am)
So, Bipasha’s ride from 11:30 am to 12:30 am must be Ride 2 amounting Rs 50
Also, Anjali’s second ride must be Ride-3 from 12 pm to 1 pm (without any wait and total spending of Rs 50 by 12:15 pm)
Also, Bipasha’s other two rides cannot be Ride-3 as it should be completed by 1 pm
From point 4, the last ride taken by Anjali and Bipasha was the same
Let’s say Anjali’s last ride was Ride-4 from 1 pm to 2 pm just after Ride-3 taken from 12 pm to 1 pm as Anjali never took a break mentioned
So, for Bipasha’s last ride, she could have reached 1:30 pm and taken the Ride-4 from 2 pm to 3 pm after 30 mins wait for Anjali
So, Bipasha’s second ride could be Ride-1 from 12:30 pm to 1:30 pm
But that is not possible as she took a 1-hour coffee break after completing her second ride.
Thus, this is only possible if Anjali took Ride-2 from 1 pm to 2 pm and her last ride is Ride-4 from 2 pm to 3 pm respectively
Such that Bipasha’s second ride is Ride-1 from 12:30 pm to 1:30 pm and then 1-hour coffee break from 1:30 pm to 2:30 pm and then 30 min wait for Anjali from 2:30 pm to 3 pm and finally the last ride, Ride-4 from 3 pm to 4 pm
The rest of the information can be gathered as follows-
18. Which ride was taken by all three visitors?
- Ride-4
- Ride-2
- Ride-3
- Ride-1
Since the time slot varies for different visitors as well as rides, so let’s arrange the data with respect to rides vs visitors and fill the time slot and corresponding spending accordingly.
From point 1, Chitra spend Rs 50 and completed her rides by 11 am without any wait, so she must have taken 2 rides Ride-1 (Rs 20) and Ride-3 (Rs 30)
From point 2, Anjali took Ride-1 at 11 am after waiting for Chitra to complete, so Chitra took Ride-3 from 9 am to 10 am and Ride-1 from 10 am to 11 am respectively
From point 3, Bipasha first of three rides is from 11:30 am to 12:30 pm
Also, by 12:15 pm, all three have spent same amount = Rs 50 each (same as Chitra’s complete spending by 11 am)
So, Bipasha’s ride from 11:30 am to 12:30 am must be Ride 2 amounting Rs 50
Also, Anjali’s second ride must be Ride-3 from 12 pm to 1 pm (without any wait and total spending of Rs 50 by 12:15 pm)
Also, Bipasha’s other two rides cannot be Ride-3 as it should be completed by 1 pm
From point 4, the last ride taken by Anjali and Bipasha was the same
Let’s say Anjali’s last ride was Ride-4 from 1 pm to 2 pm just after Ride-3 taken from 12 pm to 1 pm as Anjali never took a break mentioned
So, for Bipasha’s last ride, she could have reached 1:30 pm and taken the Ride-4 from 2 pm to 3 pm after 30 mins wait for Anjali
So, Bipasha’s second ride could be Ride-1 from 12:30 pm to 1:30 pm
But that is not possible as she took a 1-hour coffee break after completing her second ride.
Thus, this is only possible if Anjali took Ride-2 from 1 pm to 2 pm and her last ride is Ride-4 from 2 pm to 3 pm respectively
Such that Bipasha’s second ride is Ride-1 from 12:30 pm to 1:30 pm and then 1-hour coffee break from 1:30 pm to 2:30 pm and then 30 min wait for Anjali from 2:30 pm to 3 pm and finally the last ride, Ride-4 from 3 pm to 4 pm
The rest of the information can be gathered as follows-
Ride-1 was taken by all three visitors
19. How many rides did Anjali and Chitra take in total? (type in numerical)
Since the time slot varies for different visitors as well as rides, so let’s arrange the data with respect to rides vs visitors and fill the time slot and corresponding spending accordingly.
From point 1, Chitra spend Rs 50 and completed her rides by 11 am without any wait, so she must have taken 2 rides Ride-1 (Rs 20) and Ride-3 (Rs 30)
From point 2, Anjali took Ride-1 at 11 am after waiting for Chitra to complete, so Chitra took Ride-3 from 9 am to 10 am and Ride-1 from 10 am to 11 am respectively
From point 3, Bipasha first of three rides is from 11:30 am to 12:30 pm
Also, by 12:15 pm, all three have spent same amount = Rs 50 each (same as Chitra’s complete spending by 11 am)
So, Bipasha’s ride from 11:30 am to 12:30 am must be Ride 2 amounting Rs 50
Also, Anjali’s second ride must be Ride-3 from 12 pm to 1 pm (without any wait and total spending of Rs 50 by 12:15 pm)
Also, Bipasha’s other two rides cannot be Ride-3 as it should be completed by 1 pm
From point 4, the last ride taken by Anjali and Bipasha was the same
Let’s say Anjali’s last ride was Ride-4 from 1 pm to 2 pm just after Ride-3 taken from 12 pm to 1 pm as Anjali never took a break mentioned
So, for Bipasha’s last ride, she could have reached 1:30 pm and taken the Ride-4 from 2 pm to 3 pm after 30 mins wait for Anjali
So, Bipasha’s second ride could be Ride-1 from 12:30 pm to 1:30 pm
But that is not possible as she took a 1-hour coffee break after completing her second ride.
Thus, this is only possible if Anjali took Ride-2 from 1 pm to 2 pm and her last ride is Ride-4 from 2 pm to 3 pm respectively
Such that Bipasha’s second ride is Ride-1 from 12:30 pm to 1:30 pm and then 1-hour coffee break from 1:30 pm to 2:30 pm and then 30 min wait for Anjali from 2:30 pm to 3 pm and finally the last ride, Ride-4 from 3 pm to 4 pm
The rest of the information can be gathered as follows-
Total rides taken by Anjali and Chitra = 4 + 2 = 6
20. What was the total amount spent on tickets (in Rs.) by Anjali? (type in numerical)
Since the time slot varies for different visitors as well as rides, so let’s arrange the data with respect to rides vs visitors and fill the time slot and corresponding spending accordingly.
From point 1, Chitra spend Rs 50 and completed her rides by 11 am without any wait, so she must have taken 2 rides Ride-1 (Rs 20) and Ride-3 (Rs 30)
From point 2, Anjali took Ride-1 at 11 am after waiting for Chitra to complete, so Chitra took Ride-3 from 9 am to 10 am and Ride-1 from 10 am to 11 am respectively
From point 3, Bipasha first of three rides is from 11:30 am to 12:30 pm
Also, by 12:15 pm, all three have spent same amount = Rs 50 each (same as Chitra’s complete spending by 11 am)
So, Bipasha’s ride from 11:30 am to 12:30 am must be Ride 2 amounting Rs 50
Also, Anjali’s second ride must be Ride-3 from 12 pm to 1 pm (without any wait and total spending of Rs 50 by 12:15 pm)
Also, Bipasha’s other two rides cannot be Ride-3 as it should be completed by 1 pm
From point 4, the last ride taken by Anjali and Bipasha was the same
Let’s say Anjali’s last ride was Ride-4 from 1 pm to 2 pm just after Ride-3 taken from 12 pm to 1 pm as Anjali never took a break mentioned
So, for Bipasha’s last ride, she could have reached 1:30 pm and taken the Ride-4 from 2 pm to 3 pm after 30 mins wait for Anjali
So, Bipasha’s second ride could be Ride-1 from 12:30 pm to 1:30 pm
But that is not possible as she took a 1-hour coffee break after completing her second ride.
Thus, this is only possible if Anjali took Ride-2 from 1 pm to 2 pm and her last ride is Ride-4 from 2 pm to 3 pm respectively
Such that Bipasha’s second ride is Ride-1 from 12:30 pm to 1:30 pm and then 1-hour coffee break from 1:30 pm to 2:30 pm and then 30 min wait for Anjali from 2:30 pm to 3 pm and finally the last ride, Ride-4 from 3 pm to 4 pm
The rest of the information can be gathered as follows-
The total amount spent by Anjali = Rs 140
