Let the usual time taken = t hours Given, distance, d = 60 × (t + 3.5) Next day, 2d/3 of the distance covered in t/3 of the time Remaining distance, d/3 = 40 × 2t/3 => d = 80t => 80t = 60t + 210 => t = 10.5 hours The usual scheduled arrival time = 9 AM + 10.5 hrs = 7:30 PM
- CAT Courses
- Free Video Resources & Tests
Video Resources
...
- Super 75
- CAT Past Papers
- Free Study Material
- BlogsJanuary 7, 2026
GDPI Topics for MBA: 100 Important Topics for CAT 2025–26
January 6, 2026GDPI Preparation 2025 – Complete Strategy to Convert MBA Calls
- Results














 Now, OB is circum-radius of equilateral triangle thus formed
OB = OA + AB = OA + R = (2/√3) × R
=> OA = 2R/√3 – R = (2 - √3)R/√3
Also, OC = OA + 2R = (2 - √3)R/√3 + 2R = (2 + √3)R/√3
Required ratio = OC : OA = (2 + √3)R/√3 : (2 - √3)R/√3
= (2 + √3)2 : (2 - √3)(2 + √3)
= 7 + 4√3 : 1
Now, OB is circum-radius of equilateral triangle thus formed
OB = OA + AB = OA + R = (2/√3) × R
=> OA = 2R/√3 – R = (2 - √3)R/√3
Also, OC = OA + 2R = (2 - √3)R/√3 + 2R = (2 + √3)R/√3
Required ratio = OC : OA = (2 + √3)R/√3 : (2 - √3)R/√3
= (2 + √3)2 : (2 - √3)(2 + √3)
= 7 + 4√3 : 1


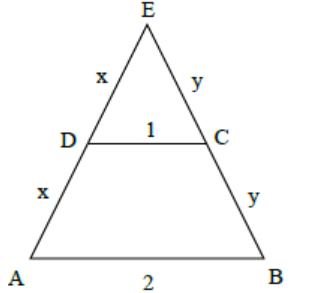 Given perimeter of trapezium ABCD = 6
=> AB + BC + CD + DA = 6
Let BC = y and DA = x
=> 2 + y + 1 + x = 6
=> x + y = 3
Since, AB//CD and CD = 1/2 AB
=> D is mid-points of AE
and C is mid-point of BE
So, DE = x = AD
And CE = y = BC
Perimeter of AEB
= AB + BE + AE
= 2 + 2y + 2x
= 2 + 2(x + y)
= 8 units
Given perimeter of trapezium ABCD = 6
=> AB + BC + CD + DA = 6
Let BC = y and DA = x
=> 2 + y + 1 + x = 6
=> x + y = 3
Since, AB//CD and CD = 1/2 AB
=> D is mid-points of AE
and C is mid-point of BE
So, DE = x = AD
And CE = y = BC
Perimeter of AEB
= AB + BE + AE
= 2 + 2y + 2x
= 2 + 2(x + y)
= 8 units


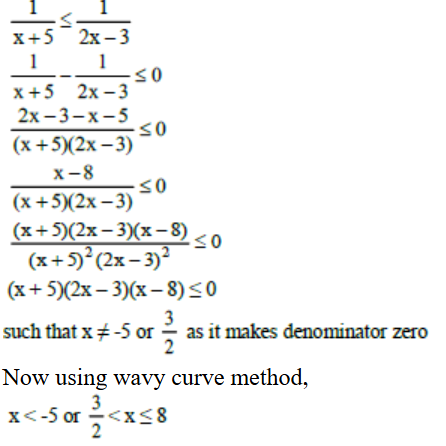

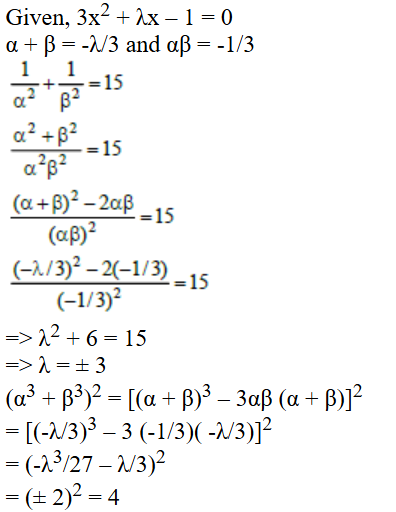

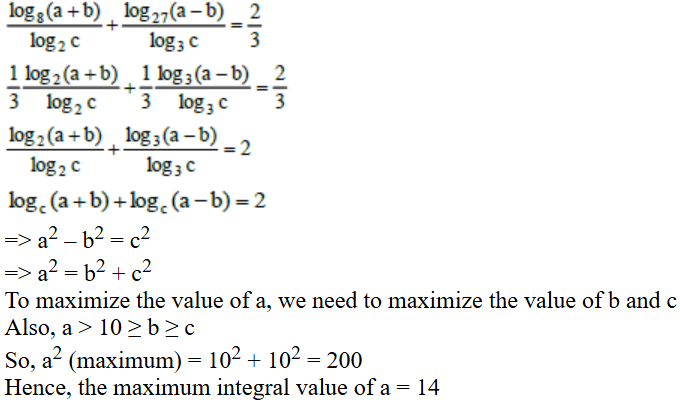


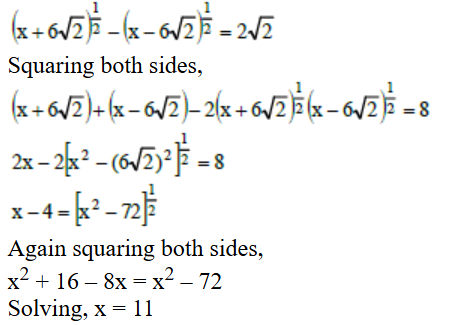
 Given, paths between P to Q to S + paths between P to R to S + paths between P to Q to R to S
= 3 × 4 + 4 × q + 3 × p × q = 62
=> 4q + 3pq = 50
=> q (4 + 3p) = 50
Possible values, q = 2 and p = 7 or q = 5 and p = 2
Also, paths between Q to R + paths between Q to P to R + paths between Q to S to R
= p + 3 × 4 + 4 × q = 27
=> p + 4q = 15
Now, q = 2 and p = 7 satisfies
Hence, the number of direct paths between Q and R = p = 7
Given, paths between P to Q to S + paths between P to R to S + paths between P to Q to R to S
= 3 × 4 + 4 × q + 3 × p × q = 62
=> 4q + 3pq = 50
=> q (4 + 3p) = 50
Possible values, q = 2 and p = 7 or q = 5 and p = 2
Also, paths between Q to R + paths between Q to P to R + paths between Q to S to R
= p + 3 × 4 + 4 × q = 27
=> p + 4q = 15
Now, q = 2 and p = 7 satisfies
Hence, the number of direct paths between Q and R = p = 7